Codeforces Round #256 — Разбор

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Решение:7139559

Так как награды одного типа можно ставить на одну полку, то посчитаем общее количество кубков a и общее количество медалей b. Чтобы узнать минимальное количество полок, которое потребуется например для кубков, можно посмотреть на целую часть дроби a / 5 и учесть остаток. Но можно воспользоваться и более лаконичной формулой: (a + 5 - 1) / 5. Аналогично считается и минимальное количество полок для медалей: (b + 10 - 1) / 10. Если сумма этих величин превосходит n, то разместить награды нельзя, иначе можно.

448B - Про суффиксные структуры

Решение:7139584

Рассмотрим каждый случай отдельно. При использовании только суффиксного автомата от строки останется какая-то её подпоследовательность. Проверить, является ли t подпоследовательностью s можно разными способами, но самый простой и самый быстрый — известный метод двух указателей. При использовании только суффиксного массива можно добится любой перестановки символов исходной строки. Если вам не очевидно это, советую подумать, почему это так. Тем самым s и t должны быть анаграммами. Так ли это, можно проверить, посчитав количество каждой буквы в обоих строках. Если каждая буква входит в s столько же, сколько и в t, то это анаграммы. Осталось проверить случай применения обоих структур. Общая стратегия здесь такая: удалить ненужные символы и сделать нужную перестановку. Так ли это, можно проверить похожим образом, как и со случаем анаграмм, но каждая буква должна входить в s не меньшее число раз, чем в t. Если же ниодна проверка не выполнилась, то получить t из s невозможно. Итоговая сложность O(|s| + |t| + 26).

448C - Про покраску забора

Решение:7139610

Для решения нужно понять несколько простых вещей. Например, каждая горизонтальная полоса должна быть как можно шире, то есть не упираться своими краями в другие полосы, так как иначе будет не оптимально. Вторая мысль — под каждой горизонтальной полосой могут быть только горизонтальные полосы, так как опять же, иначе это не оптимально. По-этому, если низ забора будет покрашен горизонтальным мазком, то этих мазков должно быть не менее min(a₁, a₂, ..., a_n). Эти мазки красят низ забора и, возможно, разбивают забор на несколько непокрашенных несвязных частей. Для каждой из этих частей нужно вызвать решение, учитывая что некоторая нижняя часть забора покрашена, и проссумировать эти значения. Теперь понятно, что функция рекурсивная — ей передаются границы отрезка l, r (часть забора) и уже покрашеная горизонтальными мазками высота h. Но нужно не забыть ещё про один вариант — когда нет горизонтальных мазков и все доски красятся вертикально. Это означает что ответ на отрезке следует ограничить числом r - l + 1. При данных ограничениях на n минимальный элемент на отрезке можно находить наивно, пробекаясь по отрезку [l, r]. Суммарная сложность в этом случае составит O(n²). Но если использовать для нахождения минимума например, дерево отрезков, то можно добиться сложности O(nlogn).

448D - Про таблицу умножения

Решение:7139620

Воспользуемся бинарным поиском по ответу. Нам нужно найти такое максимальное x, что количество чисел из таблицы, меньших x, строго меньше k. Чтобы посчитать это количество для фиксированного x, просуммируем количество меньших чисел в каждой строке. В i-й строке их будет 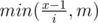$\text{[math]}$ . Тем самым итоговая сложность — O(nlog(nm)).

448E - Про делители

Решение:7139644

Научимся превращать X_i в X_i + 1. Для этого нужно действовать по определению и конкатенировать списки делителей каждого элемента X_i. Чтобы это сделать эффективно, предпосчитаем все делители числа X (потому что для любого i, X_i будет состоять только из его делителей). Это можно сделать стандартным методом за 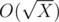$\text{[math]}$ . Как посчитать делители делителей? Нужно знать, что для данных в задаче ограничений на X, максимальное количество делителей D(X) будет 6720 (у числа 963761198400), а значит, делители делителей можно посчитать за O(D²(X)). Имея эти списки, можно превратить X_i в X_i + 1 за время O(N), где N = 10⁵ — ограничение на количество элементов в выводе. Теперь научимся превращать X_i в X_2i. Что нам говорит последовательность X_i? Помимо того, куда перейдёт X за i шагов, она может сказать, куда перейдёт каждый делитель числа X за i - 1 шаг. На самом деле, X_i является конкатенацией всех Y_i - 1, где Y — делители X. Например, 10₃ = [1, 1, 1, 2, 1, 1, 5, 1, 1, 2, 1, 5, 1, 2, 5, 10] = [1] + [1, 1, 2] + [1, 1, 5] + [1, 1, 2, 1, 5, 1, 2, 5, 10] = 1₂ + 2₂ + 5₂ + 10₂. Как узнать какой отрезок соответствует какому-то Y? Пусть pos(Y) — позиция первого вхождения числа Y в X_i. Тогда нужный отрезок будет начинаться в pos(prev(Y)) + 1, а заканчиваться в pos(Y). prev(Y) — это предыдущий перед Y делитель X (если их упорядочить по возрастанию). Итак, чтобы получить X_2i из X_i, нужно для каждого элемента знать, куда он перейдёт за i шагов. Мы знаем его делители — это один шаг, а для каждого делителя знаем, куда он перейдёт за i - 1 шаг. Тем самым, нужно сконкатенировать нужные отрезки в определённом порядке. Это так же можно сделать за O(N). Как теперь найти X_k для любого k? Способ похож на алгоритм быстрого возведения числа в целую степень:

при k = 0 X_k = [X],

при нечётном k выполнить переход от X_k - 1 к X_k,

при чётном k выполнить переход от X_k / 2 к X_k.

Такой метод делает O(logk) итераций. Кстати, так как при X > 1 последовательность X_k будет иметь префикс из k единиц, то k можно ограничить числом N. Итоговая сложность составит 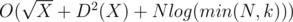$\text{[math]}$ .

int f(int l, int r, int offset) find the minimum element from l to r, call it m suppose we paint m horizontal rows from bottom for each (l,r) which are not yet painted apply f(l, r, offset + m) add this quantity to m return m or r - l + 1, whichever is smaller

ll arr[6000]; ll n; ll rec_func(ll l,ll r,ll h){ if (l==r) return 1; if (l>r) return 0; ll mini=1e9; for (ll i=l;i<=r;i++) mini=min(mini,arr[i]-h); ll ans=mini; ll p1=l; for(ll i=l;i<=r;i++){ if (p1<=i){ if (arr[i]-h==mini) {ans+=rec_func(p1,i-1,h+mini);p1=i+1;}} } if (p1<=n-1) ans+=rec_func(p1,n-1,h+mini); return min(ans,r-l+1); } int main() { // your code goes here cin>>n; for (int i=0;i<n;i++) cin>>arr[i]; cout<< rec_func(0,n-1,0)<<endl; return 0; }

Комментарии (116)

Показать архивные | Написать комментарий?

__Spiral__

10 лет назад, # |

+30

great contest!

→ Ответить

oversolver

10 лет назад, # ^ |

+23

Thanks, man.

vinamilk

← Rev. 2 →

lol, comment from someone who didn't participate. btw, problem C was great :)

ilidar

he could be one of those gray guys...

subway

Question C was awesome..!!

ashishmalik007

← Rev. 3 →

-26

S.Ged

+14

first of all you should print YES instead of Yes

IWillBeRed

Sorry, but in your code nothing is right..

Mn619

6 лет назад, # ^ |

So u red now?

~~~~~ Your code here... ~~~~~

catlak_profesor_mfb

-19

simply everything with this code is wrong. You have so many variables lol

I_love_Coding

I think you should check your coding convention before public you code

JCPWFLOI

it was a really great contest and it's a pity that i don't have time to read Problem E.

Какие-то странные комментарии чекера в Е:

wrong answer 1st lines differ - expected: '1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ... 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ', found: '1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ... 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 '

Lelby

Ну, посередине значит где-то ошибка, где у чекера в выводе многоточие...

Timur_Sitdikov

+10

Задача D, совсем мелкая поправка формулы: не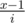 $\text{[math]}$ , а min( 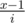$\text{[math]}$ , m).

Спасибо!

kuangbin

+27

great contest! The problem is very nice! Thank you! what a pity it is DIV2 only.

is this round rated or not? i can't see the change of my rating.

div2 is rated, div1 is unrated

92anurag

can anybody please tell whats wrong with my approch in C ... please help .. http://mirror.codeforces.com/contest/448/submission/7138159

try this case :

1 3 3 2 2 3 3 2 1 1

i am getting 4 as the output ... is it right??

ImaDra

Yes.

xiangel

10 5 5 5 5 5 2 5 5 5 5 the answer should be 8.

yahya.elfakir

Can anyone explain problem C for me please? how is it O(n²)???

Please can anyone give me more details for problem C solution?? how is it O(n²)?

in each segment [l,r] you should find minimum element O(n) and by dividing you have at most n segment to solve

assume this test:

9 8 7 6 5 4 3 2 1

You have to track h: the height of painted bottom too no?? and 1<h<10^9 :/

the solution's order is not related to h

assume you got [1,n] , there is two cases : 1. you paint horizontally : in this case the number of strokes is min(a[1,n])

and next you should solve some new segments 2. you paint them all vertically

5 1 2 2 1 2

if you paint horizontally you have these segments : [2,3] and [5,5] then you should solve them seperately

5 8 7 6 5 4

you first solve [1,5] >> [1,4] >> [1,3] >> [1,2] >> [1,1]

Thank you for the time you gave me now i've got it :D

paradoXXX

+11

Пытаюсь открыть решение автора по задаче D. Выводится сообщение — "Недостаточно прав для просмотра данной страницы"

Спасибо, поправил.

Gogis

Just a small grammar mistake: (problem D) "In i th row their will be..." I think you meant "there." But anyway, great tutorial (I'm totally not a grammar nazi :D).

Tiger_zinda_hai

How can i view solution of these problems.I am new to codeforces.

When you enter the contest standings, you can see anybody's solution to any problem.

shohaghsust

problems are great and very interesting....

great contest..problems are very interesting...

suryasumanth1

please anyone explain briefly how to solve problem C .... i didn't understood the editorial. please!!!

kayesjay

← Rev. 4 →

Here's a general idea: Suppose we have a recursive function f(l, r) that gives us the minimum number of ways to paint the fence (And hence the solution that we are looking for is f(1,n)). Note that you can paint the fence using only vertical strokes, which takes r-l+1 strokes and hence f(l,r) <= r - l + 1.

In order to use the horizontal strokes optimally, we need to paint the fence from the bottom most row to the maximum row that we can paint using one stroke. For example, for the configuration [2, 2, 3, 4, 2, 3, 2], it is only optimal if we paint the bottom 2 rows if we were to use horizontal strokes at all. Otherwise we will be better off using vertical strokes.

Using the same example, upon painting the bottom two rows, we are left with the array [0, 0, 1, 2, 0, 1, 0]. Now we call the recursive function on f(3, 4) and f(6, 6) to paint what is remaining on the fence. Of course, we need to remember the amount of rows which we have already painted when we recurse. Here's a pseudocode for the recursive function.

something like this: 7134060

ka16

Thank for your clear explanation! Small typo: f(l,r) <= r-l+1, due to the definition of f(l,r) as the minimum number of ways.

green-tea

8 лет назад, # ^ |

-8

Brilliant explanation. Much better than what was given in editorial.

__builtin__wolfy

Trying to understand solution of 448C - Painting Fence. oversolver does this part build the segment tree iteratively?

    a[n] = 2e9;
    for(d=1;d<n;d<<=1);
    for(int i=0;i<n;++i) t[i+d]=i;
    for(int i=n+d;i<d+d;++i) t[i]=n;
    for(int i=d-1;i;--i) t[i]=a[t[i*2]]<a[t[i*2+1]]?t[i*2]:t[i*2+1];

Codephile

Yes !. You can also build segment tree with recursion but each node should keep track the index of minimum elements in range. 7140283

-11

I know that segment tree requires O(4 * n) space but he's using an array of size n. How is that possible?

pachon

Since you only need to do queries (and no updates) you can use sparse data table, that can be constructed iteratively. Sparse data table

Thanks. Down-vote logic is a mess on this website.

Nice problems, thanks you !.

THAT70sSHOW

Can anyone please elaborate a bit more on the approach to solve problem D ?

Assuming that you already know binary search, the idea is simple, at least for me. The multiplication table looks like:

i|                  |elements < x|
1|1 2 3  4  5  6 ...|(x-1)/1     |
2|2 4 6  8 10 12 ...|(x-1)/2     |
3|3 6 9 12 15 18 ...|(x-1)/3     |
. . .

Let f(x) the number of elements on the multiplication table that are less than x. f can be compute by iterating each row and check how many numbers are less than x, that is (x-1)/i, but you have to remember that you only have m columns, so you take min(m,(x-1)/i). With binary search we want to find largest x so that f(x) < k. Hope it was clear

Killever

Great, Thanks for your neat explanation

Thank you for clearing my doubt and a neat explaination. +1

haleyk100198

Thanks a lot pachon, I wasn't so sure where did the (x-1)/i pop up from until I saw your table. :D

palash1993

4 года назад, # ^ |

Thanks for clarification. But i did not understand how l-1 is our answer because l=1 and h = n*m+1. And all elements between this range are not part of multiplicable table.

Can you point out to what code are you referring to?

In my case, back then I submitted this.

I use variables lo, hi variables for the while loop.

I would say that in binary search you need to find a range that allows you to handle all possible cases and still returns the correct answer. Depending on your conditions you can use a lo variable with 0, 1, -INF, -1, ... the sames hold for hi variable.

In this problem, I used the hi = n*m + 1 just to handle some cases like 1 1 1. Also if you check other participant's code you can see that in binary search is common to return lo - 1 if after a halving range operation you are setting your lo = mid + 1, conversely you should return lo + 1 if you set lo = mid - 1.

YourRatzon

Спасибо за замечательный раунд!!

jibon_ebong_shomoy

can someone tell me why my approach is not correct. I decrease the heights of the plank in each stroke. First , I can give a horizontal or vertical strip. Now , from pos 1 I find the first segment whose left and right planks are completely painted. at first it is the whole segment 1...n . Now I check , if the maximum height in this segment is less than (r-l) , then I give a horizontal stroke and I subtract 1 from all the planks in the segment. Or else I stroke the highest plank vertically , and set its height to INF. now I continue this until I have every plank either 0 or INF. Here is my code ,7140267

Contest was really great! I enjoyed the problem D. However, I did not understand the code of the problem C, maybe someone has solution without segment tree?

There is a recursive solution using divide and conquer as mentioned by the author. I solved it using this approach My submission : 7140132

yoones.rezaei

There was a o(n^2) DP solution.

If you dont like segment tree, just replace rmq(l,r) to min_element(a+l,a+r+1)-a in my solution:)

Oh, thanks. Now I understood)

Nooor

oversolver thank you for these interesting problems, I don't understand why we're seeking for the minimum element in the segment

a+l, a+r+1

instead of

a+l, a+r

any clarification would be so appreciated, thanks in advance

All its ok, we find minimun in [l,r], it is just signature of standart c++ function like sort or reverse, right bound always is not included.

MrDindows

+18

Как по мне, задача Е проще решается следующей рекурсией:

go(x, k):
	if (k == 0 or x == 1):
		print x
	else	
		foreach (d in divisors(x)):
			go(d, k-1)

Ну и обрубать её надо, если вывели N чисел. Такая рекурсия сделает не более 2N шагов, так как каждый шаг, где x не равен 1, вызывает шаг с выводом 1. Соответственно от логарифма в асимптотике избавляемся.

Да, это проще. И, кажется, все участники так и решали, но захотелось поделиться и своим решением.

Hi there.

about problem D. what is the necessity that the answer from binary search could be built by two integer 1<=i<=n & 1<=j<=m ?

it may be a large prime number(larger than n , m) .

etal

I came up with a O(n^2) DP solution for C,suboptimal asymptotics but may be simpler to code. Let v[pos][h] be the minimum # of strokes to paint from stick 'pos' onwards and with horizontal bars coming from the left up to height h. Then:

-If h>height[pos] h=height[pos] (bars higher than height[pos] stop)

-Now the solution is simply the minimum of:

painting vertical:1+v[pos+1][h]

painting horizontal (only if height[pos]<n, it can't be the solution): height[pos]-h+v[pos+1][height[pos]]

yoones.rezaei did you do the same?

kalimm

In problem C here is a my code on contest. http://mirror.codeforces.com/contest/448/submission/7136746

My min variable is global!

Just changed it to local, i took accepted. http://mirror.codeforces.com/contest/448/submission/7142429

What a pity :(

Nice implementation.

You really made my day, thanks gentleman!

pobelter

Is it possible to solve C using a O(nlogn) greedy method?

while(not finished){
if (# of units covered if we paint horizontally > # of units covered if we paint vertically)
paint horizontally
else
paint vertically
}

chaotic_iak

I'm not sure whether there's a smaller counterexample, but 5 4 5 4 5 4 5 breaks your solution. The best solution is to paint all vertical strokes (7 strokes), but your solution will begin by painting four horizontal strokes at the bottom followed by four more to clear the "spikes" (8 strokes).

mxh1999

For problem D,I have an another idea.But it may be wrong. We can divide the number into n blocks. In block i,the numbers are bigger than i*m and smaller than (i+1)*m; We can know the k-th largest number is in which block. Then we sort the number int the block and find the number. The complexity may be O(mlogn+mlogm) It is not as good as solution but I think it's also an idea. Please think it carefully instead of disliking it simply.

I dont understand this solution from this part

and find the number

← Rev. 6 →

Err...Maybe my English is too poor T_T. It means like this: 1 2 3 4, 2 4 6 8, 3 6 9 12, The number in first block is 1 2 2 3 3,in second block is 4 6 6.And in third block is 8 9 12. We can find the number in each line which is in the block like what you said. And know the k-th largest number is in which block. Then we copy them to an array and sort.

oh, yes, now this patr i understand.

but how you find kth number in block? for example first block (with n=m=500000) contains 6638449 elements. Second — about 6 millions.

Oh,It seems that I am wrong. I didn't realize there will be so many numbers in a block in the contest. I only think it will be similar to m.

It's really a good problem.Thank you very much!

caioaao

Original idea in edit. Saw that my idea was completely wrong, lol

just to be clear that I know there are lots of improvements that can be done (linear sort on diagonals, binary search to find the diagonal in which the item stands), but i thought an O(m*log m) solution would be fine and easier to code in contest time

Regarding the problem D, I still don't understand why in the solution code we don't need to check if the number is in the multiplication table. Can someone please explain?

There are n*m numbers in the multiplication table. k <= n*m . So the number must be in the multiplication table. Tip:if a*b=c*d,they can be counted twice instead of only once.

Take the 2x3 table, then 5 <= 2*3 is not in the table, isn't it? My question is about the answer from binary search, i.e. l-1. Why is it always in the table?

Suppose that we have found the answer x that is not in the table. This element has the L numbers less than it. But since it is not in the table, then there is a greater element with the same number of smaller elements L, and thus a contradiction, because we have to find the maximum such x.

Oh,yes. But I think it's not a problem. If you search 5.you will only let l=5 or r=5 instead of printing 5. In binary search,l and r may be not in the table at first.but they will be right in the end.

I'm not sure if I understand your comments correctly. But, we can prove the binary search solution, i.e. l-1 is included in the table as follows: At the end of binary search loop, l is the number that satisfies count(l) >= k and count(l-1) <= k-1, then l-1 has to be included in the table, otherwise those two conditions never hold. That means, l-1 is in the table and count(l-1) = k-1. Then l-1 is the k-largest number.

mochow

Please someone explain the solution of problem D properly. Can't understand a thing. :(

Here you go: http://mirror.codeforces.com/blog/entry/13063#comment-178268

Thanks a lot kayesjay! Understood. :D

vkozlovs

-6

контест ***** он мне жизнь сломал

I_love_Varechka

vkozlovs а может пора задуматься и обвинять не задачи а себя.

code_overlord

In 448E - Divisors, can someone explain better how to make X_2i from X_i? I don't understand the wording in the editorial!

arjunarul

← Rev. 8 →

"Actually, X_i is concatenation of all Y_i - 1, where Y is divisor of X. For example, 10₃ = [1,1,1,2,1,1,5,1,1,2,1,5,1,2,5,10] = [1] + [1,1,2] + [1,1,5] + [1,1,2,1,5,1,2,5,10] = 1₂ + 2₂ + 5₂ + 10₂."

As I see it, this is the crux of the problem. I'll try to put this in different words:

Let the divisors of X be D₁, D₂,.., D_k, in increasing order. So, X₁ = [D₁, D₂, .., D_k] Now, you can take each of these D_i separately, transform them i - 1 times independently to get (D₁)_i - 1, (D₂)_i - 1, etc and then concatenate those to get X_i. ie, X_i = (D₁)_i - 1 + (D₂)_i - 1 + .. + (D_k)_i - 1

Now, suppose you have X_i, and you also know which segments correspond to (D₁)_i - 1, which correspond to (D₂)_i - 1, etc. Now, you want to get X_2i. First, you transform X_i to X_i + 1. Now, you take the first element from X_i + 1. This will be a divisor of X. Let it be D_j. From the previous step, you already know (D_j)_i - 1. So, take that and shove it into X_2i. Now, take the second element of X_i + 1 and repeat the same. Keep doing this till you get the first 10⁵ elements of X_2i.

Now, all we need to do is figure out is which segment of X_i corresponds to (D₁)_i - 1, etc. That is explained here: "How to know which segment corresponds for some Y? Lets pos(Y) be the first index of Y in X_i. Then needed segment starts from pos(prev(Y)) + 1 and ends in pos(Y), where prev(Y) is previous divisor before Y in sorted list of divisors." Replace Y with D_j and prev(Y) with D_j - 1. I think this part is explained clearly in the editorial itself. See the 10 example.

rsFalse

Solving B using regexps ( O(|s|*|t|)+ ), language — Perl: 7157269

yomin

Well,Problem 448D — Multiplication Table. I've got binary search solution for python. But it is Time limit exceeded. Can't we use python ? My solution ID 7400257

My solution ID:7400257

VladaMG98

Excuse me, but how we can achieve O(NlogN) in Painting Fence. Yeah, with segment tree we can find minimum in interval[l,r], but (atleast I think so) we need to have indexes of all the minimums inside that interval, so we'll have to iterate that, which bring us to complexity of O(N^2). Am i wrong?

Thanks in advance. :)

Firstly, we need only one index. After finding that index we call recursion to [L,ind-1] and [ind+1,R]. If you draw recursion tree with these segments you will see that tree have exactly N vertices. In every vertex we need O(N) or O(logN) time for search.

accidentallygivenfuck

I wonder how you found that 963761198400 in 448E - Divisors?

It is just a typical problem :)

TomBombadil

Editorials like these with their incomprehensible English make me want to kill the editorial writer,,, slowly and painfully.

Good luck

Great contest though. Cheers.

GiveMinus

give me — please :)

a very silly contest

hunter1703

8 лет назад, # |

My solution

Can anyone explain to me what is wrong with my solution?? Need help plz.

eggeek

7 лет назад, # |

How do you define 'k-th largest number' ?

In sample: 2 3 4

the matrix is:

1 2 3

2 4 6

all sorted numbers are: 6, 4, 3, 2, 2, 1

the 1st largest number is 6, the 2nd largest number is 4, the 3rd largest number is 3, the 4th largest number is 2, so the answer should be 2. Why the answer is 3?

Kognition

Wow, yeah, so the English in this problem was absolutely terrible. It is actually looking for the k-th smallest number, not the k-th largest. It describes picking the k-th number from a non-decreasing list of the integers, but that is literally what k-th smallest means. Fortunately, if you just do k = n*m+1-k in the beginning, it should fix your code, but it gave me trouble for a good while trying to understand what it meant.

Vaidik_Patel_27

6 лет назад, # |

All the 5 que are very fantastic. Especially last 3 que are very very great.

Salute for question setter. Thank you.

TheOmniscient

5 лет назад, # |

Doubt regarding 448D- Multiplication Table

In question Multiplication table, what happens when the binary search chooses a number that does not belong in the multiplication table matrix of m*n? How does the tutorial solution escape that situation to give the correct result?

confusedman

Didn't understand this either... the number could easily be a prime greater than max(n,m).

The number can't be a prime. All elements in the table, except for row (1, j) and column (i, 1) where i,j are within the range (1 ... n) and (1 ... m) respectively, are a product of two numbers i*j and the problem asks for the k-th out of all of them.

towrist

4 года назад, # |

Very Interesting: my idea for Problem E was completely different from the editorial. I noticed that for $$$k\leq10^3$$$, we can just do naive brute force and it will easily pass ($$$10^8$$$ operations). For $$$k>10^5$$$, we can just print $$$10^5$$$ ones.

The interesting case is when $$$10^3\leq k\leq 10^5$$$. Here, I observed that it is always enough to consider only all factors upto the first non-prime factor of $$$X$$$. And we can easily deduce the array for primes, and also for composite numbers which are either just product of two primes or $$$p^2$$$, for some prime $$$p$$$. It is exactly composite numbers of this forms which are the first non-prime factor of any number. The rest is just concatenation.

Here is my solution: 97098735

amansahore09

2 года назад, # |

Can anyone explain why TLE occurs in the following code for problem C?

2 года назад, # ^ |

if (p1<=n-1) ans+=rec_func(p1,n-1,h+mini); you need r instead of n-1

Блог пользователя oversolver

Doubt regarding 448D- Multiplication Table