selfcompiler's blog

ZQUERY
By selfcompiler, 10 years ago, In English

Hii I am trying to solve this problem http://www.spoj.com/problems/ZQUERY/ after thinking so many days i am not able to come up with efficient solution ,would any one like to suggest some idea, how to solve this ?

  • Vote: I like it
  • 0
  • Vote: I do not like it

Comments Comments (11)
| Write comment?
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Obviously, you can sort the queries to solve the problem offline and use prefix sums to covert the question to "longest subarray with S[l] = S[r], L ≤ l ≤ r ≤ R.

Then, you can increase R and keep the answers for all L; it's just a matter of updating these answers when R is incremented. It can be done in .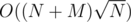

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    @Xellos Thanks , can you explain more how to solve efficiently to find the longest subarray with S[l]=S[r] ,L<=l<=r<=R,

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    can you please explain the part keep answer for all L?

    → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

First we use this Mo's algorithm to sort Query.

http://mirror.codeforces.com/blog/entry/7383

Let's call each group is a "bucket"

For each Query, we have to find i j which s[i] = s[j] and L<=i<=j<=R

Each i j has 3 cases :

  1. i and j in bucket, so we can for, just O(sqrt(n))

  2. i in bucket, j out of bucket. Let's call id1[s[j]]=j is the max position of s[j]. So answer is max(id1[s[i]]-i)

  3. i and j out of bucket. Similar, call id2[s[j]]=j is the min position of s[j], so answer is max(id1[s[j]]-id2[s[j]])

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I_love_PMK can you explain bit more after query sorting step ?

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Let's p = sqrt(n)

      Every query has L <= p is in bucket 1

      p < L <= 2*p is in bucket 2....

      With every query in the same bucket, sort query with increasing of R.

      → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I have solved it with MO's algorithm + segment tree for keeping track of the maximum value . Complexity is O( (N + M) * ROOT(N) * LOG (N) ) .

Here is the implementation http://ideone.com/YayNX7.

It would be good is someone can tell how to solve without the segment tree in O( (N + M) * ROOT(N) ).

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Could you please explain how did you solve it??

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Have a look at codechef march challenge problem: qchef , it has a nice and detailed editorial.

      → Reply
»
9 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Here is a editorial to a different problem with a similar solution.

→ Reply