Hii I am trying to solve this problem http://www.spoj.com/problems/ZQUERY/ after thinking so many days i am not able to come up with efficient solution ,would any one like to suggest some idea, how to solve this ?
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
32:40:12
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
32:40:12
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 08:54:48 (j2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Obviously, you can sort the queries to solve the problem offline and use prefix sums to covert the question to "longest subarray with S[l] = S[r], L ≤ l ≤ r ≤ R.
Then, you can increase R and keep the answers for all L; it's just a matter of updating these answers when R is incremented. It can be done in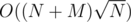 .
.
@Xellos Thanks , can you explain more how to solve efficiently to find the longest subarray with S[l]=S[r] ,L<=l<=r<=R,
can you please explain the part keep answer for all L?
First we use this Mo's algorithm to sort Query.
http://mirror.codeforces.com/blog/entry/7383
Let's call each group is a "bucket"
For each Query, we have to find i j which s[i] = s[j] and L<=i<=j<=R
Each i j has 3 cases :
i and j in bucket, so we can for, just O(sqrt(n))
i in bucket, j out of bucket. Let's call id1[s[j]]=j is the max position of s[j]. So answer is max(id1[s[i]]-i)
i and j out of bucket. Similar, call id2[s[j]]=j is the min position of s[j], so answer is max(id1[s[j]]-id2[s[j]])
I_love_PMK can you explain bit more after query sorting step ?
Let's p = sqrt(n)
Every query has L <= p is in bucket 1
p < L <= 2*p is in bucket 2....
With every query in the same bucket, sort query with increasing of R.
I have solved it with MO's algorithm + segment tree for keeping track of the maximum value . Complexity is O( (N + M) * ROOT(N) * LOG (N) ) .
Here is the implementation http://ideone.com/YayNX7.
It would be good is someone can tell how to solve without the segment tree in O( (N + M) * ROOT(N) ).
Could you please explain how did you solve it??
Have a look at codechef march challenge problem: qchef , it has a nice and detailed editorial.
Thanks Everyone now it is solved :)
Here is a editorial to a different problem with a similar solution.