Всем привет!

Как некоторые уже знают, на этих летних сборах в Петрозаводске droptable презентовал новую структуру данных, а именно дерево палиндромов. Я имел честь поучаствовать в изучении структуры за полгода до этого, о чём и хочу теперь рассказать :)

Но для начала краткий экскурс. Если вы уже знаете базовые идеи реализации, можете смело переходить к интересной части. Давайте каждому палиндрому поставим в однозначное соответствие строку, равную его правой половине, то есть, радиус и булеву переменную, обозначающую его чётность. Теперь объединим все радиусы подпалиндромов строки S в два бора — для чётных и нечётных длин раздельно. Утверждение: такой бор будет занимать 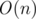памяти. Ну действительно, в строке может быть не больше n^[1] различных палиндромов, а каждая вершина в дереве соответствует одному уникальному подпалиндромы. Следовательно, у нас не больше n + 2 вершин.

Покажем, что такую структуру можно построить за 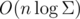. Давайте для каждой вершины в дереве хранить суффиксную ссылку, которая ведёт в вершину, которая соответствует радиусу максимального суффикс-палиндрома всего палиндрома текущей вершины. Так, например, есть вершина, соответствующая радиусу "bacaba" нечётной длины, то есть, палиндрому "abacabacaba". Суффиксная ссылка будет ввести в вершину, соответствующую радиусу максимального суффикс-палиндрома "abacaba", то есть, в "caba".

Теперь допустим, что у нас есть дерево палиндромов для строки S и мы хотим добавить в конец строки какой-то символ. Будем поддерживать указатель на состояние, соответствующее максимальному суффикс-палиндрому. Дальнейшие действия аналогичны таковым при построении суффиксного автомата. Мы смотрим на новый символ строки и на тот, который в строке стоит непосредственно перед палиндромом, которому соответствует текущее состояние. Если они не совпадают, то переходим по суффиксной ссылке и повторяем проверку. Когда они совпали, мы смотрим на то, существует ли переход по новому символу из состояния. Если есть, то переходим и радуемся, иначе палиндром, который мы должны добавить раньше не встречался в строке. Создаём для него новое состояние. Теперь нужно посчитать для него суфф ссылку. Ну, собственно, переходим по суффиксным ссылкам снова, пока не найдём второй корректный переход по такому же символу. Когда мы его нашли — это и есть суфф ссылка для нового состояния. Всё это чудо работает амортизированно за 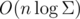, так как на каждом этапе мы сперва несколько раз сокращаем нашу текущую строку, а затем увеличиваем её всего лишь на один символ. А сокращений, очевидно, будет не больше, чем расширений (которых не больше, чем n).

Да, несколько слов о реализации. Вы могли заметить, что я не рассматриваю случая, когда происходит выпадение за пределы автомата. Это связано с тем, что такого выпадения никогда и не бывает. Как этого достичь — так как у нас есть два бора, у нас есть два корня. Для одного из них выставим начальную длину 0 (для чётных палиндромов), а для второго — -1 (соответственно для нечётных). И по-умолчанию делаем суффиксную ссылку из первого во второй. Таким образом, каждый раз, когда мы оказываемся в корне с длиной -1, мы всегда обнаружим, что переход возможен, так как новый символ и символ перед суффикс-палиндромом будут совпадать.

Код: link
Написан мной в виде, наиболее похожем на суффиксный автомат с целью более лёгкого запоминания :). Есть также замечательная реализация от Merkurev link.

Теперь я расскажу о том, как же вообще так получилось, что я имел отношение к подготовке задачи с петрозаводских сборов. В комментариях к моей статье про алгоритм Манакера droptable написал про онлайновую версию алгоритма и попросил добавить её в статью, что я и сделал после некоторых обсуждений. Как раз тогда Михаил сказал мне про задачу с APIO, который, по удивительному стечению обстоятельств, проходил в то же время, в которой нужно было использовать алгоритм Манакера с некоторыми суфф структурами. Вкратце условие: найти для строки рефрен-палиндром.

Тогда Михаил намекнул, что у них есть классное решение, которое быстро и просто решает ту задачу. Так как я был юн и неопытен и ещё совсем не разбирался в суффиксных структурах, я решил подумать над тем, что же за такое конструктивное альтернативное решение могло быть у этой задачи. Так я в некоторой степени заново изобрёл дерево палиндромов :) На самом деле тогда я был весьма далёк от решения, т.к. не использовал суфф ссылки, а дерево хотел строить хешами, но тем не менее общую структуру я придумал. И когда на радостях рассказал её Михаилу, оказалось, что именно такая структура была у них :)

Далее было много плодотворных обсуждений, результатами которых я бы хотел поделиться. Так, например, я придумал способ строить дерево за 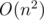, который, впрочем, на практике оказался быстрее некоторых алгоритмов с другими структурами, работающими за линию. Идея была похожа на онлайновый алгоритм Манакера — в каждой ячейке массива храним указатель на вершину, которой соответствует максимальный палиндром с центром в ней. Далее при пересчёте палиндрома в новой ячейке, мы берём либо вершину из симметричной к ней вершины относительно текущего максимального суффикс-палиндрома, либо некоторого её предка с меньшей длиной, если она "вылазит" за край строки. Изначально мне казалось, что решение выйдет линейный даже если просто подниматься вверх до нужного уровня каждый раз, но оказалось, что это не так :(

Используя технику двоичного подъёма, мне удалось снизить оценку до . Существуют алгоритмы нахождения LA (Level Ancestor) за , которые позволили бы решать ту задачу за 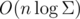, но, очевидно, это было бы неразумным ввиду сложности. (Да, именно чтобы выяснить это я создал эту статью). Отсюда следует...

challenge 1: Можете ли вы довести идею алгоритма до линии, не используя общие методы поиска LA?

Код:
: link
: link

Как ни странно, это ещё не всё, о чём я хотел рассказать. В изначальной версии задачи, которую планировалось дать на Петрозаводск нужно было не только добавлять символ в конец строки и считать количество новых палиндромов, но и, подумать только, удалять символ с конца строки. Позже эта часть была упразднена в виду и без того высокой сложности задачи. Теперь же я хотел бы описать возможные алгоритмы решения той задачи, которая должна была быть изначально.

Для начала поймём — что же составляет проблему для нас? Вроде бы у нас всё быстро работает, почему бы просто не делать откат на прошлое состояние? Однако, такой вывод ложный, ведь оценка добавления нового символа 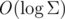амортизированная. А если мы, допустим, возьмём строку aaaaaaa...aab, а потом начнём каждый раз удалять и возвращать b. Легко видеть, что при каждом возвращении мы будем совершать 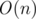итераций, что, конечно, недопустимо. Все три метода, которые будут описаны несут в себе цель сделать оценку обновлений при добавлении символа строгой, а не амортизированной. Итак:

1) "Умные" суффиксные ссылки. Давайте в каждой вершине хранить дополнительно суффиксную ссылку, которая ведёт в вершину, которой в строке предшествует не та же самая буква, что и обычной суфф ссылке нашей вершины и использовать эти две ссылки для переходов. Согласно лемме 11 из статьи droptable (статья пока не выпущена, однако, уже принята к печати. С ней вскоре будут выступать на этой конференции), путь до корня по "умным" ссылкам будет проходить через 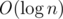вершин. Таким образом, каждый раз мы будем делать не больше 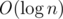операций.

2) Полный автомат. Раз уж на то пошло, зачем нам париться со сложными теоремами и одной ссылкой, которая ведёт на другую букву? Давайте хранить в каждой вершине массив на 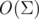элементов — по одной такой ссылке для каждой буквы в алфавите. Легко показать, что можно теперь отвечать на запросы за 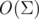. Пускай мы добавляем к строке символ 't'^[2]. Это будет иметь примерно такой вид:

v = last
v = smartlink[v][t]
new = to[v][t]
v = smartlink[v][t]
suflink[new] = to[v][t]
smartlink[new] = smartlink[ suflink[new] ]
smartlink[new][p] = suflink[new]

Теперь мы можем решать задачу за 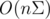времени и памяти улучшим результат до 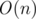и 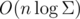. Для этого нам понадобится персистентный массив. Его можно построить на основе дерева отрезков. Итак, создаём персистентное дерево отрезков на Σ элементов. Далее при создании новой вершины, форкаем за нужный корень дерева и за 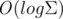делаем соответствующее изменение. Вот наша быстрая структура и готова.

3) Дерево предпалиндромов. Рассматривался также вариант хранения дерева, которое хранит палиндромы + предпалиндромы, то есть, строки, которым не хватает одного символа, чтобы стать палиндромом. Это также позволяло решать задачу быстро, но структура выходила слишком сложной. В итоге от неё отказались, а некоторые полезные наработки перекочевали в первый описанный здесь алгоритм.

Challenge 2: Видите ли вы другие способы решения поставленной задачи? Например, сохранение амортизированной оценки при удалении или другие способы решать задачу быстрее, чем за ?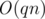

На десерт я хочу предложить вам потренироваться в использовании этой структуры и попробовать решить две задачи. Первая из них — та самая задача, которая была предложена этим летом на петрозаводских сборах, но с более серьёзными ограничениями. К слову, тогда её сдала всего одна команда. IMCS of Siberian FU Bizons какой-то ужасной битовой магией сверхужали по памяти суффиксный автомат и сдали его с первой попытки за три минуты до конца контеста. Почёт им и уважение :). Вторая же задача уже довольно старая. Впервые она была представлена на зимних сборах школьников 2006 года, где авторское решение предполагало сведение задачи к LCA на автомате префикс-функции строки. Однако...

Challenge 3: Предлагаем вам решить её в несколько другой интерпретации, в которой авторское решение, по видимому, уже не сработает. Представьте, что первой строкой вам даётся та строка, которая должна идти второй, а во второй вам дан генератор. Необходимо посчитать ответ для каждого его префикса. Дерзайте :)

Итак, задачи:
timus. Палиндромы и сверхспособности
e-olimp. Фабрика палиндромов

[1]Докажем по индукции — рассмотрим какой-то префикс строки и добавим к нему 1 произвольный символ. Утверждается, что у нас может появиться только один новый палиндром. Ну рассмотрим строку s[0..k + 1] и её максимальный суффикс-палиндром. Очевидно, он такой один. При добавлении нового символа любой новый палиндром будет суффиксом строки. Утверждается, что новым уникальным может быть только максимальный из них. Ну допустим, это не так. Для каждого суффикса в палиндроме верно, что он является перевёрнутым префиксом. Теперь посмотрим на префикс в максимальном суффикс-палиндроме, равный по длине немаксимальному суффикс-палиндрому, который, предположительно, новый. Он будет равен этому самому немаксимальному суффикс-палиндрому. Приходим к противоречию.

[2] 'p' — символ перед вершиной в суффиксной ссылке. Это значение, очевидно, легко поддерживать вместо со списком вершин. smartlink — умные ссылки для всех символов. to — таблица переходов вершины. suflink — классическая суффиксная ссылка вершины. last — вершина, в которой мы были до добавления символа. new — вершина, в которой мы окажемся. Если её нет, то создаём.