We have tree with n vertexes and we can cover this tree with k simple paths (paths can overlap). How many vertexes we can cover?
k < = n < = 106
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
We have tree with n vertexes and we can cover this tree with k simple paths (paths can overlap). How many vertexes we can cover?
k < = n < = 106
| Название |
|---|



Nice problem, thanks for posting it. Here is my solution:
1) Note that the answer will always end in the leafs.
2) If the number of leafs is smaller or equal than 2·k we can mark all the tree (task: proof).
3) Make the tree rooted, with any non-leaf vertex as a root.
4) Take leafs greedy, every time choosing the vertex that will cover the highest amount of new vertices. (task: proof)
UPD: I fogot to tell about the complexity, it's O(n), as the only thing we need is to build the heavy-light decomposition, where we call the deepest-going edge heavy.
Step 4) is also O(N)?
This looks like an upgrade of a Gym trainings' problem (S2E8, problem F, I made an editorial of that round). The tree was rooted there and we only picked paths from the root; it can be solved with a max-segtree. Here, maybe we could prove that if we root it at the centroid, the paths could be taken in a smart way (crossing the centroid) so that it reduced to that problem...
Just run a single dfs from the root. When going to the deepest child continue the path that led to the current vertice, otherwise start the new path. Now you have no more than n paths, with length no more than N and you are to select 2·k - 1 maximum.
Ok, u should also count the depth of all subtrees first, but that's still O(n) =)
I also came up with your 3 first points, but 4 seems unclear to me. We take leafs greedy choosing the path the highest amount of new vertices? There is a counterexample: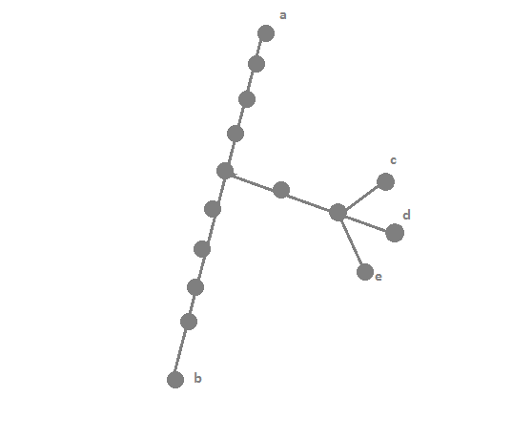
With k = 2 greedly we would take a-b and a-d (or -c or -e), but we can take a-c and b-e
My idea was to choose 2·k leafs in the way to maximize the vertext-cover of the subtree. I already see the mistake in my solution, but it's minor and easy to fix. Let's make the root not a non-leaf vertice, but the leaf that is guaranteed to form one of the correct answers, for example the end of any diameter. After this we should only choose 2·k - 1 leaf.
On your example this works in the following way:
1) Name the vertex a as a root.
2) Take the vertex b and add 10 to the answer.
3) Take any from {c, d, e} and add 3 to the answer.
4) Take any remaining from {c, d, e} and add 1 to the answer.
5) We now have {a, b, c, d} selected, and could cover subtree they form.
I got the idea, but still don't know how to do it in O(n)
Aaah, almost 9 years have passed since this problem appeared at the Polish Olympiad -- Subway.
Let's partition the tree into layers -- leaves form the first layer, nodes at distance 1 from any leaf form the second layer and so on. Let's denote by l the number of layers and by si the size of the i-th layer. Then the answer is: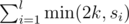 .
.
To see why this works first notice, that the above sum is an upper bound on the answer. Then try to construct the set of paths, the size of which actually matches the bound.
link to polish olympiad question is not working, anywhere else can I find it ?