К каждой задаче присутствует challenge — бонусная задача на тему, которую можно порешать just for fun и обсудить в комментариях. =)
Переберем все элементы, которые можем выкинуть, пройдем по оставшимся элементам и посчитаем максимальную разность среди соседних. Это решение имеет сложность O(n2). Можно заметить, что при удалении элемента ответ либо не поменялся, либо стал равен разности тех элементов, которые являлись соседями только что удаленного, поэтому ответ можно получить за O(1), а итоговое решение будет иметь сложность O(n). Ограничения позволяли сдать любое из этих решений или даже менее эффективное.
Challenge: пусть мы удаляем не один элемент, а k любых элементов (первый и последний, как и раньше, удалять нельзя). Какую минимальную максимальную разность между соседними элементами мы можем получить? Решите задачу в ограничениях 1 ≤ k ≤ n - 2, n ≤ 105, ai ≤ 109.
Заметим, что нам неважно, в каком порядке применяются операции: мы можем сперва выполнить все сдвиги, а затем все прибавления. После n сдвигов мы получаем исходную последовательность, поэтому достаточно рассмотреть только варианты, где сдвиги выполняются менее n раз. Аналогично, после десяти прибавлений единицы ко всем цифрам получим исходную последовательность, поэтому рассмотрим только варианты, где прибавления выполняются менее десяти раз. Для каждого из 10n вариантов определим результат применения всех операций; сохраним лучший результат и для каждого из вариантов сравним с лучшим. Сравнения осуществляются за O(n) операций, поэтому итоговое количество элементарных операций имеет порядок 10n2. От константы 10 можно избавиться, если заметить, что при фиксированном сдвиге первую цифру всегда выгодно сделать нулем, и это однозначно определяет количество прибавлений; однако, чтобы сдать задачу, эта оптимизация не требовалась.
Challenge: можете ли вы решить задачу за время  ? O(n)?
? O(n)?
496C - Удаление столбцов/497A - Удаление столбцов
Посмотрим на первый столбец таблицы. Если буквы в нем не упорядочены по алфавиту сверху вниз, его нельзя оставить ни в каком корректном варианте оставить некоторые столбцы. С другой стороны, пусть буквы в первом столбце упорядочены, но в ответ мы его не взяли. Добавим его к ответу; несложно видеть, что в новом варианте оставить столбцы все строки также упорядочены сверху вниз по алфавиту.
Будем рассматривать столбцы слева направо. Если мы попробовали добавить текущий столбец к ответу и лексикографический порядок строк где-то нарушился, мы обязаны его удалить; если же все в порядке, возьмем его в ответ. Рассуждение, аналогичное предыдущему абзацу, показывает, что такой жадный алгоритм приводит к оптимальному (и более того, единственному среди оптимальных) ответу. Итоговая сложность — O(n2).
Challenge: сколько существует таблиц n × m, для которых ответ на эту задачу равен k? Придумайте как можно более оптимальное решение.
496D - Игра в теннис/497B - Игра в теннис
Фиксируем t; теперь мы можем проэмулировать ход партии и убедиться, что запись является корректной, а также определить соответствующее s; выведем все подходящие пары s и t. Такое решение работает за O(n2), попробуем его соптимизировать.
Если после окончания очередного сета мы обработали k розыгрышей, то позицию окончания следующего сета можно определить так: найти t-ую позицию после k-ой, в которой записано 1, аналогично, найдем t-ую позицию, содержащую 2. Если позиция t-ой единицы встретилась раньше, то следующий сет выигрывает первый игрок, и позиция окончания сета совпадает с позицией t-ой единицы; аналогично разбирается случай, если раньше идет t-ая двойка. Если партия еще не кончилась, но в оставшейся части и единиц, и двоек менее t, то запись некорректна. Позицию t-ой единицы или двойки после заданной позиции можно определять за  бинпоиском, или за O(1) при помощи предподсчитанного массива позиций.
бинпоиском, или за O(1) при помощи предподсчитанного массива позиций.
Теперь заметим, что для данного t партия из n розыгрышей не может содержать больше n / t сетов, поскольку каждый из них содержит как минимум t розыгрышей. Если мы просуммируем количество сетов в партии по всем возможным t, мы получим не более 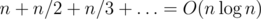 (известная сумма гармонического ряда). В зависимости от способа обработки одного сета итоговая сложность составляет
(известная сумма гармонического ряда). В зависимости от способа обработки одного сета итоговая сложность составляет 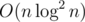 либо
либо  ; любой из этих способов с запасом укладывается в ограничение.
; любой из этих способов с запасом укладывается в ограничение.
Очевидно, что для каждого t существует не более одного варианта s; однако, для данного s может существовать более одного варианта t. Первый тест с таким случаем — претест 12. В условии требуется выводить ответ в лексикографическом порядке пар; здесь легко допустить ошибку и вывести пары с равными s по убыванию t (если в конце просто переворачивать массив).
Challenge: при подготовке этой задачи я столкнулся с тем, что не могу построить тест с большим количеством пар в ответе; в тестах к задаче максимальное количество — 128 = количество делителей числа 83160. Сможете ли вы побить этот рекорд? Хвастайтесь в комментариях, сколько пар вы умеете получать при n ≤ 105; если у вас есть соображения, как оценить максимальное количество пар теоретически, тоже прошу делиться.
496E - Распределение партий/497C - Распределение партий
Отсортируем все партии и всех актеров вместе по возрастанию нижней границы (при равенстве сначала идут все актеры, потом все партии); пойдем в этом порядке по возрастанию нижней границы. Будем поддерживать множество актеров, которые уже <<начались>>, т.е. встретились в этом порядке раньше; если мы встретили актера, добавим его в это множество. Если мы встретили партию (aj, bj), из множества допустимых актеров нам нужно выбрать такого, у которого di ≥ bj (требование ci ≤ aj гарантируется тем, что i-ый актер встретился раньше, чем j-ая партия); если таких актеров в множестве нет, мы не можем получить ответ. Если таких актеров несколько, нам выгоднее брать того из них, у которого di минимально (интуитивно, он нам в дальнейшем меньше пригодится). Сопоставим текущую партию выбранному актеру и уменьшим его ki на единицу; если теперь ki = 0, мы больше не можем пользоваться этим актером и должны выкинуть его из множества.
Чтобы уложиться в ограничения, множество текущих актеров приходится поддерживать в эффективной структуре данных (например, std::set или декартово дерево). Сложность итогового решения 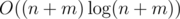 .
.
Challenge: пусть каждая песня присутствует в количестве qj (1 ≤ qj ≤ 109), и каждой копии надо сопоставить своего актера. можете ли вы решить задачу в тех же ограничениях (поскольку ответ теперь очень большой, достаточно проверить его существование)?
Если в какой-то момент произошло столкновение, это значит, что какая-то вершина одного из многоугольников попала на одну из сторон другого многоугольника. Рассмотрим систему отсчета, в которой многоугольник A неподвижен. В этой системе многоугольник B перемещается параллельно сам себе, и каждая его точка описывает окружность. Если мы пересечем все окружности, которые описывают вершины B, со всеми сторонами A, мы можем проверить, попадает ли какая-то из вершин B на границу A. Аналогично, перейдем в систему отсчета, связанную с B, и проверим, попадает ли вершина A на границу B. Ограничения на координаты позволяют выполнять проверки абсолютно точно.
Другой подход к тому же самому по сути решению: пусть в системе отсчета, связанной с A, произошло столкновение. Тогда выполнено векторное равенство x + y = z, где z — вектор с началом в точке P и концом где-то на границе A, x — вектор с началом в точке Q и концом где-то на границе B, y — вектор с началом в P и концом где-то на окружности с центром в P, проходящей через Q. Если переписать это равенство как y = z - x, можно увидеть, что все возможные значения z - x пробегают сумму Минковского многоугольников A и зеркального отражения B (с точностью до сдвига), y пробегает известную окружность. Сумму Минковского можно представить в виде объединения nm параллелограммов, каждый из которых — сумма двух сторон разных многоугольников; в конечном итоге, пересечем все границы всех параллелограммов с окружностью.
Сложность обоих решений — O(nm). Как указано выше, существует решение в целых числах; однако, маленькие ограничения на координаты не позволяют легко свалить решения с вещественной арифметикой. Также велик был соблазн написать неточное численное решение; мы постарались отсечь все такие решения, и в итоге ни одно из них не зашло. =)
Многие имели проблемы с 8-ым претестом. Он выглядит так (левая спираль вращается вокруг левой точки, правая вокруг правой):
Challenge: пусть мы хотим завалить решение с вещественной арифметикой. Построим тест, в котором многоугольники не сталкиваются, но проходят очень близко друг к другу. Какое минимальное положительное расстояние мы можем получить в заданных ограничениях на количество вершин и координаты?
497E - Подпоследовательности возвращаются
Пусть дана какая-то строка. Как посчитать количество ее различных подпоследовательностей? Будем приписывать символы к концу по одному и считать, сколько новых подпоследовательностей появилось. Пусть к строке s приписали символ c; в строке s + c на символ c заканчивается столько же подпоследовательностей, сколько их было всего в строке s. Если их прибавить к количеству подпоследовательностей s, каждая подпоследовательность s + c учтется по одному разу, кроме тех, которые заканчиваются на c и присутствовали в строке s: они учтутся дважды. Это приводит к следующему решению: будем хранить, сколько последовательностей заканчивается на каждый из возможных символов — cntc, тогда при добавлении символа c значение cntc надо заменить на сумму всех cnt плюс один (за пустую последовательность); ответ для всей строки равен сумме всех cnt (плюс один, если нам надо учесть пустую последовательность). Например, рассмотрим первые несколько символов строки Туе-Морса:
ε — (0, 0)
0 — ( 0 + 0 + 1 = 1, 0)
01 — (1, 1 + 0 + 1 = 2)
011 — (1, 1 + 2 + 1 = 4)
0110 — ( 1 + 4 + 1 = 6, 4)
...
Легко видеть, что если значения cnt на данном шаге выписать как координаты вектора, и добавить к ним координату, тождественно равную 1, то приписывание одного символа к строке влияет на вектор как умножение на матрицу; естественным образом сопоставим каждой строке описанную матрицу.
Рассмотрим префикс последовательности ai длины km. Если разделить его на k кусков длины km - 1, окажется, что i-ый из этих кусков может быть получен из 0-го прибавлением ко всем элементам i по модулю k. Будем насчитывать матрицы для префиксов длины km, а также для всех строк, получающихся из префикса прибавлением ко всем его элементам какого-то числа x; обозначим такую матрицу за Am, x.
Легко видеть, что при m > 0 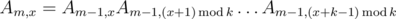 . Эта формула позволяет нам вычислить Am, x для всех
. Эта формула позволяет нам вычислить Am, x для всех 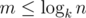 и x от 0 до k - 1 за время
и x от 0 до k - 1 за время 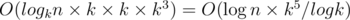 . Теперь, имея все Am, x, мы легко можем перемножить некоторые из них в нужном порядке, чтобы получить матрицу для префикса ai длины n.
. Теперь, имея все Am, x, мы легко можем перемножить некоторые из них в нужном порядке, чтобы получить матрицу для префикса ai длины n.
К сожалению, пока что решение не укладывается в ограничения по времени. Один из способов получить решающее ускорение таков: заметим, что в формуле 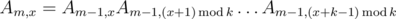 произведение можно разбить следующим образом: Am - 1, x... Am - 1, k - 1 × Am - 1, 0... Am - 1, x - 1 (если x = 0, вторая часть произведения пуста). Посчитаем для всех x произведения <<префиксов>> и <<суффиксов>> набора Am, x: Pm, x = Am, 0... Am, x - 1, Sm, x = Am, x... Am, k - 1. Теперь Am, x = Sm - 1, xPm - 1, x. Теперь вычисление Am, x для всех x при выбранном m сводится к вычислению Pm - 1, x, Sm - 1, x за O(k) умножений матриц, после чего каждый элемент Am, x вычисляется за одно перемножение. Таким образом, наше решение теперь работает за
произведение можно разбить следующим образом: Am - 1, x... Am - 1, k - 1 × Am - 1, 0... Am - 1, x - 1 (если x = 0, вторая часть произведения пуста). Посчитаем для всех x произведения <<префиксов>> и <<суффиксов>> набора Am, x: Pm, x = Am, 0... Am, x - 1, Sm, x = Am, x... Am, k - 1. Теперь Am, x = Sm - 1, xPm - 1, x. Теперь вычисление Am, x для всех x при выбранном m сводится к вычислению Pm - 1, x, Sm - 1, x за O(k) умножений матриц, после чего каждый элемент Am, x вычисляется за одно перемножение. Таким образом, наше решение теперь работает за 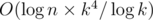 , что укладывается в ограничения с запасом.
, что укладывается в ограничения с запасом.
Challenge: решите задачу при k ≤ 100.










Ещё один классный Физтеховский контест!
Спасибо, Endagorion, за классный раунд и как всегда чудесный разбор!
А есть классные физтеховские, но не Endagorion-вские контесты?
А как же CFR232? :(
Сорри, пацаны) не писал его просто :)
Немножко саморекламы:) Анонс 262
Я уже несколько раз прочитал эту фразу и никак не могу её понять. Помогите.
Имеется ввиду, что если первый столбец упорядочен, то выгоднее его не удалять и он не испортит таблицу.
если первый столбец лексикографически упорядочен, то и все строки в таблице упорядочены, т.к. мы сначала сравниваем по первой букве, по второй, по третьей и т.д.
если уже по первой букве все строки строго упорядочены, то далее нет смысла рассматривать таблицу
Здесь имеется ввиду , что если столбец упорядочен, то мы его оставляем в таблице , и теперь будем проверять не упорядоченность очередного столбца, а упорядоченность строк, где каждая строка состоит из символов предыдущих упорядоченных столбцов и символов очередного столбца.
Вот простенькое решение: Клац...
Ребят, на задаче 496B - Секретный код на системном выдало ошибку "Ошибка тестирования", Вердикт — Runtime_Error. Кто знаком с задачей, помогите найти ошибку и не допускать впред:)
cin >> c;допишет в конец строки 0 в (n+1)-ый символ.Можна попробовать
char *c = new char [n + 1];Или считать n char-ов циклом и заменить
strcpy(l, c)наstrncpy(l, c, n);Или просто использовать
std::string:)По-моему задача A (div. 2) — задача с только что прошедшего USACO BRONZE, разве что сказки разные.
Да, задачи действительно очень похожи, но не думаю, что Endagorion читал последний USACO)
Мне кажется Codeforces A легче, чем USACO A. Меньше кода и предподсчета.
они только легендой отличаются и кода одинаково.
а challenge для задачи A похож на задачу из USACO SILVER
Не очень похож, т.к. в silver было достаточно двухмерного дп.
Challenge A div 2 — можно решить бин-поиском по ответу, видимо...
Challenge B div 2 — можно сразу сформировать 10 строк (все варианты прибавления +1), а потом найти минимальный цикличиский сдвиг для каждой и найти минимум среди них.
Challenge C div 2 / A div 1: можно посчитать для каждого столбца количество способов сделать его нормальным и ненормальным (динамикой). И теперь нужно выбрать к столбцов из всех и сделать их ненормальными, остальные — нормальными... Т.Е. Сk_n*(кол-во спосбов сделать столбец плохим)^k*(кол-во спосбов сделать столбец хорошим)^(n-k)
"ненормальных" столбиков может быть больше, чем k. Например тест:
cac
bbb
aca
(я не умею ставить переводы строки в комментариях, имелось ввиду 3 строки по три символа)
все очень просто
пишете так:
саспробелпробел
бббпробелпробел
асапробелпробел
и у вас все хорошо:)
Нетривиальная идея по challenge B div 2: возьмем 10 строк с разным смещением, дублируем и результат сконкатенируем через сепаратор t = 2 * s0 + @ + 2 * s1 + ... + @ + 2 * s10, где si — строка, у которой символы циклически сдвинуты на i. Построим суфф. дерево или автомат по строке t, и найдем в структуре лексико-графически наименьший путь длины n.
Can you describe how to solve 496B in O(N) or O(nlogn)?
Finding the lexographically smallest rotation of a string using suffix array is O(n).. and one can construct a suffix array in O(n) so it can be done in 10n i.e O(n)
Lyndon decomposition can find smallest rotation of a string in O(n) too, and it's more easy to coding.
Can you give some details? How to construct a suffix array in O(n)? Isn't it O(nlogn)? And how to find the smallest rotation in O(n)?
Same before, I want you to describe more clearly about algorithm to solve in complexity O(n) or O(nlogn). I dont' know how to construct a suffix array :/
For example we can construct suffix automaton on string S + S and then find the smallest substring of length n.
And the complexity is about: O(2*n * 10)?
for problem 496B Secret Combination i got wrong answer on test 11 while it gives me the expected answer on my PC here's the submission 9181590
This is the end of your answer: 00201196. This is the end of right answer: 20201196.
thx i actually solved it. the problem was i thought that the output is the right answer and the answer is the code output :D
Can someone explain Div 2 C in english?
Basically, you have to iterate through collumns from 1 to m, and compare two consecutive elements on the same column. Now, if we have a[row][col]<a[row-1][col], then if we don't have a previous column k in the range [1,col-1] where a[row][k]>a[row-1][k], we must delete the column col and proceed to the next column.
Thanks, what is an efficient way to find that column k though?
First, you can notice than we only need the first k to satisfy this, so if a[row][k]>a[row-1][k] and if we don't delete this column, then we take an array OK[row]=1 , and from now on if a[row][col]<a[row-1][col] it won't matter as long as OK[row] is already 1.
You may translate this in Russian in case you wish that.
P.s. This is my 1st ever so ignore mistakes(not algorithmic ofc)
The problem:: We are given a table of letters and we need to ensure that any row i is NOT lexicographically less than the previous row i-1.
Operation:: We are allowed to delete any column we wish to.
Output
An integer which represents minimum number of columns that will have to be deleted to solve the problem.
STRATEGY=>GREEDY ::
We iterate from 0th column to last , deciding for each column whether it will be removed or included in our final table.
2 variables- prevtaken,prevleft which will store the index of last column which was included,removed respectively.**Both -1 initially.**
answer=number of 0s columns included :P obvio
Say a function f(i)= true if while moving down the ith column the letters are in lexicographic order and FALSE otherwise
Algorithm::start iterating from left
All those columns for which f(i)=>false&&prevtaken=>-1 are to be removed.(why? easy:p )
All those columns for which f(i)=>true are to be included(obvio? easy:P)
Now consider those columns for which f(i)=>false but prevtaken is not -1
As we iterate down this column finding the lexicographic order not satisfied, if for these 2 rows,if the elements in prevtaken column for theese 2 rows are same then we remove this column(why? bcz otherwise the rowwise lexico order that we are interested in would have already been satisfied as prevtaken column is more significant).
Hopeefully you read the hopefully.. xD
P.s. The length is compromised so as to make it comprehensible for even a newbie.:)
http://mirror.codeforces.com/contest/496/submission/9179405
can some one explain 496E distribution of parts in english ?
Кто может мне подсказать, почему 9173914 получил time limit. Я же сделал так, как написано в разборе.
Вылазишь за границы массива:
Если увеличить размеры массивов в 2 раза, будет АС.
m1=b[d[k]+t];
d[k]+t>100100
Всем спасибо.
Можно уточнить, почему в DIV1-A итоговая сложность квадрат?
Если правильно понимаю, то n — перебор по столбцам, и подразумевается линия на каждом столбце. Но тогда не могу понять, как за n , а не nm проверить, что лексикографический порядок не нарушился.
P.S. Очень жаль, что пояснение "n до 100" пришло спустя полчаса.
Отношусь к числу тех, кто сразу понял, как решать за O(nnm), но не знал как за O(nm).
Можно для каждой пары соседних строк хранить флаг "верно ли, что нижняя строка уже лексикографически больше верхней", тогда чтобы понять, портит ли нам что-то данный столбец, достаточно смотреть только на символы внутри него.
Давайте расскажу про ситуацию с div1A.
Изначально ограничения были до 1000, но потом мы решили их уменьшить до 100, чтобы у медленных языков не было проблем со считыванием. При этом нам не пришло в голову, что сложность задачи от этого упала, потому что нам казалось, что кроме решения за квадрат ничего в общем-то больше и не придумаешь; это оказалось неправдой, потому что многие писали решение за куб.
Что касается ошибки в условии... забыли исправить, наша (скорее даже лично моя) вина, каюсь. Ошибка обнаружилась, когда люди стали пытаться ломать решения и обнаружили, что в валидаторе все-таки ограничения до 100. В общем, это самый серьезный фейл раунда, приношу извинения (и вам лично) еще раз.
Спасибо за пояснение!
А по поводу "фейла": бывает, не на деньги играем :)
Мне вот интересно, как можно доказать, что:
n + n / 2 + n / 3 + ... + n / (n — 1) + n / n <= n + (n / 2 + n / 2) + (n / 4 + n / 4 + n / 4 + n / 4) + ... = O(n log n)
Ну то есть мы заменяем все знаменатели на ближайшие меньшие степени двойки. Тогда в каждой группе сумма n, а групп примерно log n
Здорово! Тогда даже получается, что сумма последовательности несколько меньше log(n)!
А ты кэп, я смотрю.
А ты кэп, я смотрю :)
А ты кэп, я смотрю.
С твоего позволения, закончу этот балаган первым.
Эта оценка показывает, что не больше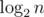 . А на самом деле примерно
. А на самом деле примерно 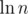 .
.
Может быть с помощью интеграла 1/x?
интеграл 1/x покажет лишь что этот ряд не сойдется.
Нет. С помощью него как раз такая сумма и считатся (а почему человека заминусовали, непонятно).
Док-во: при x от k до k + 1 1/x лежит между 1/k и 1/(k+1) Поэтому интеграл от 1/х по [1, n] лежит между 1/1 + 1/2 + ... + 1/n и 1/2 + ... + 1/(n+1). При этом мы знаем, что этот интеграл равен ln n.
Why the constrain of the problem 497A reduce the constrain?
Самое простое объяснение div1 D — через комплексные числа. Все что надо — аккуратно выписать векторы точек отрезка при вращении вокруг точки, отнять вектор второй вращающейся точки, приравнять нулю. Получаем задачу пересечения отрезка с окружностью с центром в нуле. Главное — аккуратно высчитать координаты концов отрезка, а радиус окружности всегда — расстояние между центрами вращения.
И еще по поводу точности в Div1 D. Количество вершин тут не актуально. Важны только координаты, и погрешность возникает из-за нахождения расстояния от целочисленного отрезка до начала координат. Но это несложно обойти целочисленными вычислениями или с помощью добавления и отнимания погрешности что-нибудь типа 1e-12.
How to solve the chanllenge of 496A?
Binary search on final difficulty d, then remove as many holds as you can greedily without letting difficulty exceed d.
Answer is smallest d such that you can remove at least k holds.
Um...To check if d can be achieved, can we do this? let i point to the 1st element and j to the 2nd, remove a[j] and inc j by 1 until a[j+1]-a[i] > d, then i=j, j=j+1...
That's it. Can you prove that this always achieves d with the smallest amount of holds left?
When i, j point to the 1st and 2nd hold respectively, we know that replacing j with a hold on its left wont make things better. For if you remove j after that, it is harder to remove next holder because the distance gets larger.And if you dont remove j, the situation becomes the same before replacing. Thank u, ffao, my mind is clear with this greed approach now :)
How to solve challenge problem div 2 c??
496C/497A оказалась хитрей, чем кажется :) не любой жадный за О(n^2) заходит :) на 15м тесте немало народу завалилось :)
Всем привет. Пытаюсь разобраться с задачей D (Шестерни). Как можно представить такую траекторию: "Рассмотрим систему отсчета, в которой многоугольник A неподвижен. В этой системе многоугольник B перемещается параллельно сам себе, и каждая его точка описывает окружность.", как она примерно выглядит? просто не хватает воображения))
Удобнее всего записать в координатах положение точек после поворота на угол φ. Будет c1 + (a - c1)·M(φ) = c2 + (b - c2)·M(φ), где a, b — выбранные точки, c1, c2 — центры кручения, M(φ) — матрица поворота на угол φ. Преобразование этого уравнения приводит к желаемому результату.
P.S. В комплексных числах ещё удобнее записывается.
Спасибо большое! То есть получаестя, что теперь можно выразить a через b и получить то, что нужно. А в комплексных как это можно записать?
То же самое, только вместо матрицы поворота eiφ. На мой вкус, так удобнее мыслить, чем в терминах матриц)
То, что относительно друг друга многоугольники не поворачиваются, достаточно очевидно.
В системе отсчета, связанной с A, посмотрим на точку Q. Расстояние от P до Q никогда не меняется, поэтому Q в этой системе может двигаться только по окружности, которая однозначно определяется положениями P и Q. Это определяет, как двигаются все остальные точки, поскольку Q жестко связано с B и B не поворачивается.
Сори, если туплю, но что-то не получается выразить координаты... то есть пусть a = r0+(a0-r0)*M(fi) b = r1+(b0-r1)*M(fi) c = r1+(c0-r1)*M(fi), где a — вершина A, b и с — вершины, образующие сторону многоугольника B. r0 и r1- точки, относительно которых вращаются A и B соответственно, c0 a0 и b0 — начальные положения точек a,b,c. Каким образом тут составить уравнение, чтобы получить координаты a в системе отсчёта, связанной с B?
Преобразуем ранее полученное уравнение:
c1 + (a - c1)·M(φ) = c2 + (b - c2)·M(φ).
(c1 - с2) = (b - a + c1 - c2)·M(φ).
(c1 - с2)·M - 1(φ) + c2 - c1 = b - a.
b = a + c2 - c1 + (c1 - с2)·M - 1(φ).
Таким образом, мы выразили координаты точки b — т.е. точки, которая должна лежать во втором многоугольнике, чтобы при повороте на угол φ получилось пересечение соответствующих точек. Вектор c2 - c1 у нас постоянный, а слагаемое (c1 - с2)·M - 1(φ) как раз задаёт окружность с радиусом |c2 - c1|. Центр окружности будет в точке a + c2 - c1.
А исходное уравнение берётся из условия, что точки совпадают, но там же должно быть пересечение точки и прямой?
Исходное уравнение берется из того, что точки a и b должны при повороте перейти в одну и ту же точку. После этого мы для точки a нашли множество точек b, которые при каком-то повороте с ней совпадут — это окружность. Теперь наша задача свелась к тому, чтобы эту окружность пересечь с отрезком.
А... ну всё, спасибо, теперь понятно, что происходит)) попробую накодить)
what are precomputed arrays of positions of players in 496D/497B Tennis Game Div. 1 B which reduce the complexity to O(nlogn)?
score[i] — the score of a player for the first i serves.
step[i] — how much serves are past until a player reaches the score = i.
s1 [i] = sum of points the player 1 has the index i of the main vector A1 [j] = index in the main vector that player 1 gets j points
There are the same vectors for player 2.
Using only the s1 and binary search is possible complexity n * log ^ 2 (n). Using s1 and a1 is possible complexity n * log (n).
Let a and b be two vectors containing positions in sequence where 1st and 2nd player wins respectively.
The arrays to be precomputed then are ta and tb where:
ta[i]: index in a such that a[ta[i]] > i
tb[j]: index in b such that b[tb[i]] > j
Can anyone explain in
496D - Tennis Gamewhy is itwrongto say thatnumber of valid (s,t) will be 0 if the total number of points of player who won the last point is less than or equal to another player.Because if the game is valid(i.e we have some valid s and t pair) this means the player who won it must have won
strictly moresets than other and hence more points.WA -->9231337
AC after I removed that condition --> 9231351
Not necessarily. Let, s = 2, t = 5 and consider the following score:
A B
0 5
5 4
5 4
In this case, B's total point is 13 while A's is 10, but the winner is A :)
Thnx, never thought of that :)
Div1D, why if we take A as the reference system, then the vertices on B are moving on a circle? I think the vertices on B are moving on a moving circle whose center is moving on a fixed circle. A is like sun, and B is moon, and our earth is reference system? Where am I wrong?497D - Gears
Problem D div 1:
"In this system the polygon B preserves its orientation (that is, does not rotate), and each of its vertices moves on some circle"
What circle? Can anyone give more detailed explanation? Or what should I study to understand this?
Let K be a point in polygon B. In the frame of reference in which A does not rotate, Q rotates around P in a circle (this should be easy to see).
What is a bit difficult to see is that, as the frame of reference is rotating counterclockwise around P and K is rotating clockwise around Q, K doesn't move relative to Q at all. Maybe this is easier to see with a picture:
ETA: I now noticed I accidentally switched the rotations so that Q is rotating clockwise and K is rotating counterclockwise in the picture. The principle still holds, though.
K' is where K would be after the rotation of the frame of reference. K is the final position after accounting for the fact that K is also rotating around Q with the same angular speed. As you can see, K is exactly at the same position relative to Q (directly above) in both pictures.
So K follows the exact same trajectory as Q, but with a constant translation.
Thank you. Your explanation is very clear.
Though only when 2 polygons rotate at the same angular speed, it has this nice property. What if 2 polygons rotate at different speed? How can it be solved?
I have the same approach for problem "496D — Tennis Game" and I still have TLE for test 23. Can anyone tell me why? here is my code 11077258 I have explained some steps in comments there.
How to solve the challenge version for 496E/497C
Maybe you can solve it as the simple version because it's equivalent to the reduction of an actor from 1 to Q!
497D - Gears
The Minkowski sum can be represented as a union of nm parallelograms, each of which is the Minkowski sum of a pair of sides of different polygons;But this slide mentions that to get Minkowski sum of two non-convex polygons $$$P$$$ and $$$Q$$$, at first we need to decompose $$$P$$$ and $$$Q$$$ into convex sub-polygons $$$P_1,...,P_k$$$ and $$$Q_1,...,Q_l$$$
Then we can get $$$P\oplus Q = \bigcup_{i,j}{P_i\oplus Q_j}$$$
In my solution, I triangulate both P and Q, then Minkowski sum over all pair of triangles from different polygons, and then check if the circle intersect the polygon or not, but got WA on 31(162191639).
Can you tell me, what I'm missing?
UPD: typo in the implementation of the
circle_segmentfunction.