Для каждого символа посчитаем, в какую сторону выгоднее вращать диск. Это можно сделать либо формулой: min(abs(a[i] - b[i]), 10 - abs(a[i] - b[i])), либо даже двумя циклами for: в прямом или обратном направлении.
Посчитаем количество оценок, меньших y. Если таких больше 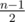 штук, то мы не сможем удовлетворить второму условию (про медиану), и ответ -1. Иначе получим ровно столько оценок y, чтобы количество оценок, больших или равных y, было как минимум
штук, то мы не сможем удовлетворить второму условию (про медиану), и ответ -1. Иначе получим ровно столько оценок y, чтобы количество оценок, больших или равных y, было как минимум 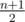 штук (возможно, это уже выполняется). Это минимальное необходимое действие для удовлетворения второго условия.
штук (возможно, это уже выполняется). Это минимальное необходимое действие для удовлетворения второго условия.
Теперь, чтобы не нарушить первое условие, сделаем оставшиеся неизвестные оценки как можно меньше — единицами, и проверим сумму. Если она больше x, то ответ снова -1, иначе требуемые оценки найдены.
Я выделил здесь три случая, хотя некоторые из них можно объединить.
- Если начальная и конечная клетка совпадают, посмотрим на количество целых соседей этой клетки. Если есть хотя бы один целый сосед, то пойдем туда и сразу же вернемся обратно, выполнив задачу — в этом случае ответ YES.
- Если начальная и конечная клетка являются соседями, то посмотрим на тип конечной клетки. Если конечная клетка треснувшая, то ответ YES. Иначе для положительного ответа необходимо, чтобы у нее был хотя бы один целый сосед — пойдем на конечную клетку, затем на этого целого соседа, а потом вернемся обратно.
- В наиболее общем случае проверим, существует ли путь по целым клеткам от начальной клетки до конечной. Если нет, то ответ NO. Иначе посмотрим на тип конечной клетки. Если она целая, то для существования ответа необходимо наличие у нее двух целых соседей — по одному мы придем в нее, а второй используем как промежуточную точку, а если конечная клетка треснувшая, то у нее должен существовать один целый сосед.
540D - Остров невезения (мой код: http://pastebin.com/3s6dRK3A)
Будем считать величину dp[r][s][p] — вероятность возникновения ситуации, когда в живых осталось r камней, s ножниц и p бумаг — для всех возможных значений r, s, p. Начальная вероятность равна 1, а для подсчета остальных необходимо сделать переходы.
Пусть у нас имеется r камней, s ножниц и p бумаг. Найдем для примера вероятность того, что в этой ситуации камень убьет ножницы — остальные две вероятности считаются симметрично. Количество случаев, в которых кто-нибудь умрет, равно rs + rp + sp, а количество случаев, в которых умрут ножницы, равно rs. Так как все случаи равновероятны, нужная нам вероятность равна 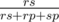 . Именно с этой вероятностью мы перейдем в состояние dp[r][s — 1][p], где ножниц станет на 1 меньше.
. Именно с этой вероятностью мы перейдем в состояние dp[r][s — 1][p], где ножниц станет на 1 меньше.
В конце, чтобы получить вероятность, что, например, камень выживет, надо просуммировать все величины dp[i][0][0] для i от 1 до r (аналогично для остальных видов).
540E - Бесконечные инверсии (мой код: http://pastebin.com/QFEMRbNP)
Запомним, на какой позиции какое число будет стоять после выполнения всех swap-ов. Теперь будем считать ответ. Ответ состоит из двух частей. Первая часть — это инверсии, образованные исключительно теми элементами, которые поучаствовали в swap-ах. Их можно посчитать одним из двух стандартных способов: mergesort-ом или с помощью сжатия координат и дерева Фенвика. Вторая часть — это инверсии, в которых один из элементов пары участвовал в swap-ах, а второй — нет. Для простоты рассмотрим тест:
2
2 6
4 8
Перестановка будет выглядеть так: [1 6 3 8 5 2 7 4 9 ...], а массив swap-нутых элементов так: [6 8 2 4].
Давайте поймем, с какими элементами будет образовывать инверсии число 8. Очевидно, такими элементами могут быть лишь те элементы, которые находятся между начальной позицией числа 8 (где сейчас число 4), и текущей его позицией. Вот этот подотрезок: [5 2 7]. Чисел на этом подотрезке, которые не участвовали в swap-ах, две штуки: 5 и 7. Число 2 учитывать не надо — ведь оно участвовало в swap-ах, и мы его посчитали на первом шаге решения.
Таким образом, надо взять количество чисел между начальной и конечной позицией числа 8 в глобальной перестановке (т.е. 8 - 4 - 1 = 3), и вычесть из него количество чисел между позициями числа 8 в массиве swap-ов (т.е. 4 - 2 - 1 = 1). Чтобы избавиться от дополнительного вычитания единицы, можно просто из правого индекса вычитать левый. Так мы получим количество инверсий, образованные элементом 8 и элементами глобальной перестановки, не участвовавших в swap-ах. Для завершения второго шага надо лишь посчитать эту величину для всех чисел, участвовавших в swap-ах. Все операции второго шага можно выполнить при помощи сортировок и бинарного поиска.











Задача С очень понравилась! Спасибо автору!
Пора учить теорию вероятностей заново :( Не смог догадаться до этой очевидной формулы.
Обидней когда придумал, и не закодил.
Не спорю. Но придумать — уже половина дела.
Это ещё что по сравнению с тем что придумал, закодил, не успел отладить, контест закончился, на дорешивании исправил пару символов и сдал.
Обидно, когда придумал, закодил, но не догадался, что в ответ пойдёт сумма :(
Well, I think, it would be great if the meanings of 'global sequence' and 'swaps array' is made clear in E's explanation (in paragraph 4 if the test case isn't counted). Do they mean 'the permutation' and 'the swapped elements' in the second paragraph...?
Yeah, "global sequence" == "permutation" and "swaps array" == "the swapped elements" (fixed)
Thanks for fixing, and thanks for the short & clear explanation!
Thanks for the editorial! If I may ask quickly about question B, I'm still a bit confused as to how the (n-1)/2 check works for the median. For example if given original grades 3, 5, 6 and minimum median of 6, with value k=50 and x=999, wouldn't it be easy to add 50 values to {3, 5, 6} such that the median exceeds 6 and sum<999? Yet with the editorial it says if at least (n-1)/2 marks are less than the median ie: (3-1)/2 = 1, marks are <= median (which there are since 3, 5, and 6 are <=6}, how does it mean we can return -1?
Thanks, sorry if this is a dumb question, I'm just really confused.
Seems like you mistook n and k.
In the example where Vova needs 49 (the problem says it's an odd number) tests and finished 3, n = 49, and k = 3. Therefore, (n — 1) / 2 is 24 instead of 1. Then, of course, the answer is -1 if there are 24 marks that are less than y, instead of 1 :)
Oh... I see now, the variable "n" was referring to ALL the course marks and not just the ones that were currently given... I didn't read the question very well; but hoping to do better next time, thanks for the problems!
The number 3 in your formula (3-1)/2 is k, but it must be n, I think that's where you are wrong.
Вроде строго меньших. Медиана должна быть больше либо равна y.
Исправил.
Edit: No need to read this. I have caught my mistake. A reading error :) One more Question for Problem B. If suppose the input is n=5 and k=3 and the minimum median is 4 and the given input is 444. So this fails the (n-1)/2 condition, but still 44444 for example is a solution (assuming sum is large enough). Sorry if it is dumb question(hopefully it is not) :) Did not read the solution carefully. My mistake. No need to reply to this.
This mistake was fixed about 30 minutes ago, maybe you haven't updated the page since that time? Now that statement says about elements less than y.
Yes, I just refreshed and saw that. Then I updated my post, thinking I read wrong. But thanks, I did not read wrong and now it has been corrected. :)
In problem D, if all the meetings are equiprobable the probability that we have minus one scissor would not be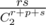 instead of
instead of 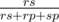 . Why we don't count the meetings between the same kind?
. Why we don't count the meetings between the same kind?
It's a conditional probability: the probability of the fact that rock kills scissors, given that somebody dies.
But the question D says any two random individuals meet so why isn't 2 people from whole set included as said above by Empty.I mean why is that wrong if we consider the whole people left as our sample space for choosing two people.
If two of the same types are chosen, we are back with the same state as before: nothing changes. We just go again, and we keep going until different types are chosen. Until that happens, nothing changes so the same state is preserved.
As dalex said, we only calculate probabilities of the different events given that something changes.
But, it will not affect the result of the probabilities?, it would be interesting to see a math proof to show how it works.
What's confusing is that we are conditioning this on the fact that a single type wins, and also we are not at all interested in the number of trials this takes. Meaning, we aren't checking the probability of the case that all three types remain (ie: they keep meeting each other).
So now, given that after some number of trials, a single type remains, we can effectively ignore all the trials where the same type meets.
Again, we could not do this if we were calculating things like:
1) number of trials until a specific type wins 2) probability that a single type will win given the possibility of an eternal tie
I get the same meaning like Empty said.I can't get the correctly example answer in my way.I think in most cases, you should read the problem without ambiguity or less.
math proof can be following:
first, lets say that
Crsp — all possible permutations of r s and p pairs.
Crr, Css, Cpp — all possible permutations between (r and r), (s and s), (p and p) pairs respectively.
Crs, Csp, Crp — all possible permutations between (r and s), (s and p), (r and p)
(note that Crs = r *s, Csp = s * p, Crp = r * p)
it's evident that
Crsp = Crr + Css + Cpp + Crs + Csp + Crp
now lets say that
Prsp — is a probability for [r, s, p]
Pr1sp — is a probability [r — 1, s, p]
Prs1p — is a probability [r, s — 1, p]
Prsp1 — is a probability [r, s, p — 1]
note that meetings between r and r, s and s, p and p doesn't remove anything, so:
Prsp = (Prsp * (Crr + Css + Cpp) + Pr1sp * Crp + Prs1p * Crs + Prsp1 * Csp) / Crsp
multiply the equation by Crsp and move Prsp * (Crr + Css + Cpp) to the left part:
Prsp * (Crsp — Crr — Css — Cpp) = Pr1sp * Crp + Prs1p * Crs + Prsp1 * Csp
but Crsp = Crr + Css + Cpp + Crs + Csp + Crp, so:
Prsp * (Crs + Csp + Crp) = Pr1sp * Crp + Prs1p * Crs + Prsp1 * Csp
or:
Prsp = (Pr1sp * Crp + Prs1p * Crs + Prsp1 * Csp) / (Crs + Csp + Crp)
finally we know that Crs = r *s, Csp = s * p, Crp = r * p, so:
Prsp = (Pr1sp * (r * p) + Prs1p * (r * s) + Prsp1 * (s * p)) / (r * s + s * p + r * p)
Nice. We obtain a recursive relation for Prsp. I mean Prsp = A * Prsp + something, a seemingly infinite recursion.
I didn't use the conditional probability at all. See my code:10949419. I'm considering all possible pairs of meeting (the sample space is n*(n-1) / 2). However, I still got the same result. When 2 people of the same species meet, no one will die. This will lead to an infinite geometrics series when you calculate the probability that someone dies.
[Edit] So, both methods are fine. If you do it without the conditional probability, but get a different result, you're calculating the probability wrong.
p[i — 1][j][k] += ppp / (1 — ppp2); can you please explain what i am doing by this ppp / (1 — ppp2); ?
Let's say we're interested in P[a rock dies].
Case 1: a rock dies in the first meeting. P(1) = i * k / space(i + j + k)
Case 2: no one dies in the first meeting, then a rock dies in the second meeting. P(2) = P[no one dies] * P(1).
Case 3: no one dies in the first 2 meetings, then a rock dies in the third meeting. P(3) = P[no one dies]^2 * P(1).
...
P[no one dies] = (space(i) + space(j) + space(k)) / space(i + j + k) = ppp2.
So, P[a rock dies] = P(1) + P(2) + ... = P(1) + ppp2 * P(1) + ppp2^2 * P(1) + ppp2^3 * P(1) + ... = P(1) / (1 — ppp2).
Sorry for my bad question, but why P(1) + ppp2 * P(1) + ppp2^2 * P(1) + ppp2^3 * P(1) + ... = P(1) / (1 — ppp2) ?
It's a geometric series.
I will see it. Thanks a lot !
Hey, why can't we use this recurrence relation instead: Considering dp[i][j][k] to be a struct with member functions r,s,p
dp[i][j][k].r= 1/3.0 *( dp[i][j][k-1].r + dp[i][j-1][k].r + dp[i-1][j][k].r);
Why is this logically incorrect?
EDIT: Got it. All are taken different. I was taking all the rocks as same.
Для чего в задаче B нужен параметр p во входных данных?) Чтобы запутать нас? :)
Да, Такое достаточно часто бывает, но если бы не было условия y <= p, то можно было бы скосить некоторую часть решений, т.к. нужно было бы брать оценку min(y, p), а не просто y. Лично я, не дочитав условие, написал min(y, p). Но из здравого смысла, действительно, медиана не может быть больше максимальной оценки, иначе — безысходность :С
Why my solution for D print wrong answer? I don't see anything different compared to the author's code.
10958659
10961000
It should be i,j,k in bound checking and counting chances
Thanks a lot!
can someone help me to correct my algorithms for Problem-B(School Marks)
My SoutionSolution
I just want to give you an advice (because I'm not familiar with Java). Your code is a bit complicated, to make it simpler, put the answer(s) to the problem into an array (or a vector). It is much easier to read, and of course, to write the code.
Here is my C++ solution (with comments) for reference: pastebin
Good luck!:)
Thanks for the fast tutorial :)
can anyone please explain how to calculate the probability in problem D?
In problems C this case 7 1 X . . . X . . 5 1 3 1 Will fall at the beginning, and will not come up So the answer should be NO, but why the answer is YES Can you explain it ?
From the statement: "the ice on the starting cell is initially cracked".
yes thinks. but i think starting will down , I read wrong .
Umm i may have grossly misunderstood problem C here. Probably the word 'side adjacent' or 'fall down'. Help me out here. I used the BFS in a grid technique to get my answer. However, my code gives me 'YES' for example testcase 2. According to my logic, that should right. Here is the case:
5 4 .X.. ...X X.X. .... .XX. 5 3 1 1
We can go to 1,1 from 5,3 as follows:
(5,3)->(4,3)->(4,2)->(3,2)->(2,2)->(2,1)->(1,1)
Here is my code: http://ideone.com/JS4OAU
What's the flaw?
When you reach (1, 1) for the 1st time, the ice from 'intact' become 'cracked', so you can't fall down yet. You must step on (1, 1) another time to fall down, but there's no room to do this, so the answer is 'NO'.
ALright so i've applied the concept of a BFS in a grid but my code keeps failing at Test case 21:
2 2 .. .X 2 2 1 1
Any ideas as to why it fails?
submission: http://mirror.codeforces.com/contest/540/submission/10967359
Ok, I've had a lot of submissions and i'm thinking this cannot be done by BF Ssince there is not way of determinig whether the adjacent edges have been stepped on or not. They may have been discovered but no way to determine that they have been stepped on i believe. Not unless i find the actual shortest path using BFS and backtrack. I'm completely lost. Could someone help me? Is this solvable with BFS?. Here's a C++ code:
http://mirror.codeforces.com/contest/540/submission/10968998
The insight is that you just need to find if the destination is reachable or not. It doesn't matter which path you take. Then at the destination, if you need an extra step on that, you just look around the 4 neighbors to see if at least two of them are dots. So you can move to one dot and move back again (assuming that you might step on another dot, while getting to the destination). There is also an edge case where you start from one of the 4 neighbors. In this case, you only need one dot.
And at least a neighbor dot have visited to ensure it reachable from start point
No need. We already check if the destination is reachable or not. If it's reachable, it already guarantees at least a neighbor dot has been visited or the starting point is a neighbor.
Can you please tell me what will be the answer for this case? 3 1 X . X 1 1 2 1
I think answer will be YES. Path: (1,1)->(2,1)->(1,1)->(2,1)
Accepted codes give NO.
you cannot go back to (1,1) because it's already cracked and you'll fall down.
A task I really liked thanks to its author, it moymu was easier than C. When I read the task E I said that it's light and wrote the code as it passed a retest on the system it is testing 22 test gave TL here is my code http://mirror.codeforces.com/contest/540/submission/10950774 — I solved this problem by Algorithm Fenwick. Many thanks to Maxim Akhmedov and Alexei Dergunov preparation for such an interesting round.
Can anyone tell me why am I getting WA on test 55 problem C? flag=0 if destination cell is intact, else it is 1. Solution
Can anyone please explain problem E in detail? I m not able to understand anything
Which part are you unable to understand. Do you understand the question clearly?
I tried to understand his code. CODE
Can you please tell me what he is doing in the last for loop of the main function and what is the function bs doing.
let me explain you the general approach. suppose you have the input as: 2 1 1000000000(10^9) 100 200000000(2*10^8)
you obviously cannot create an array of size 10^9. so you create an array with only the elements which were swaped. So the array : arr[] = {1 , 100 ,200000000,1000000000 } we then compress this array as arr[] = {1,2,3,4} (100 is replaced with 2,200000000 with 3,1000000000 with 4) now apply the swaps then we get arr[] = {4,3,2,1} now we need to do 2 things 1) Count the inversions in the compressed array 2) Count the inversions in the original sequence which contains all the elements. Add the results of 1 & 2 you get the answer. How to solve 1 ? We can use merge sort : http://www.geeksforgeeks.org/counting-inversions/ or using a fenwick tree : http://pavelsimo.blogspot.in/2012/09/counting-inversions-in-array-using-BIT.html. ans = 0 number of elements less that 4 and to its right = 3. ans = 3 number of elements less that 3 and to its right = 2. ans = 5 number of elements less that 2 and to its right = 1. ans = 6. so the answer for the first part is 6.
Now, How to solve the 2nd part ? (this is the last loop in the editorial solution) Getting back to our original sequence after swaping. seq = 1000000000,2,3,4,...98,99,200000000,101,102.........999999998,999999999,100,1 now how many inversions for 10^9 ? it's original position — current position so 999999999 but we have already counted the inversion made by 200000000,100,1 in the first part where they were compressed, so subtract 3.
now inversions for 2*10^8 is also calculated in the same way.
Now add the results of the 2 parts. Please go thorough the editorial code. the above is an explanation of that code. It is easy to understand.
also have a look at http://mirror.codeforces.com/blog/entry/17643#comment-225956 that is what the last loop is for
Got it. Thanks for such a detailed reply and the links.
np
Here's my code that uses fenwick trees (Binary Indexed Trees) and
lower_boundto solve this question.Can some one explain why we need to do the second part in question E. Why cant we simply count the no. Of inversions using merge sort or a fenwick tree?
I understood it after understanding the question and solution clearly.
Because you will miss cases where first number is a moved one and the other one did not move.
look at first input:
after swaps it looks like:
2,4,3,1,5....
if you just consider pairs in which both elements have moved from original you will get:
2,4,1
this will give you 2 pairs (2,1) and (4,1) but what about (4,3) ? you will only get this, by the second method that has been explained.
You cannot construct the complete tree and expect to iterate through it in timelimit that is set.
got it.Thanks :)
is it just me or anyone else?
I wanted to practice on this round but find the image in Problem C is a dead image... http://mirror.codeforces.com/predownloaded/5b/ff/5bff99f4731b22c9ea00f830072ddfe7040ed80d.png
I am trying to understand the following solution 10945934 for 2 days already.
I don't get the key part of the solution:
Could, someone please explain in as much detail as possible, how does this part of the code work?
I can provide an alternative to this one if you'd like me to :)
Sure!
I'd be glad to see a different perspective.
In problem D , i cannot understand the meeting probability . According to tutorial it's r*s / (r*s + s*p + p*r) for rock species meets/kills scissors species when they meet . Now i'm giving my view , i want to know whether it's correct or not .
Suppose at any situation we have r rocks, s scissors and p papers .
Now , let's find the probability to choose 1 rock species and 1 scissors species . say it's P(x)=(r/(r+s+p))*(s/(r+s+p-1)) . That means P(x)=(r*s)/((r+s+p)*(r+s+p-1)) .
again for 1 scissors species and 1 paper species . say it's P(y)=(s*p)/((r+s+p)*(r+s+p-1)) .
again for 1 paper species and 1 rock species. say it's P(z)=(p*r)/((r+s+p)*(r+s+p-1)) .
Now the probability of rock kills scissors = P(x) / (P(x)+P(y)+P(z)) .
it's equal to (r*s) / (r*s + s*p + p*r) . exactly the same as tutorial . Plz let me know whether i'm correct or not .