Блог пользователя zxqfl

Distributed Code Jam practice
Автор zxqfl, история, 10 лет назад, По-английски

Can anyone recommend resources for preparing for the Distributed Code Jam on June 14th? Some past problems of a similar nature would be really helpful.

  • Проголосовать: нравится
  • +31
  • Проголосовать: не нравится

»
10 лет назад, # |
← Rev. 2   Проголосовать: нравится +21 Проголосовать: не нравится

One problem which appeared in AE last year was to compute LCS of two strings up to 105 characters.

→ Ответить
»
10 лет назад, # |
  Проголосовать: нравится +24 Проголосовать: не нравится

Some Simple Problems :
Problem 1
Given a Sequence A of integers , find i and j such that A(i) + A(i+1) ...+ A(j) is Maximum/Minimum , where length of A can be upto 10^10 . TL : 1 sec
Idea
Basically , we divide A into say 10^8 lengthed 100 segments , and then process each of them on different machines and later combine the information to find the answer .
Problem 2
Given a number N as large as say 10^20 , find it`s number of divisors .
Idea
Divide the set of possible divisors <= 10^10 , into 100 groups and then add the result from each of them.

  • Some other problems can be found on this(polish site). The distributed ones are "Maksymalna podtablica", "Kółko informatyczne", and "Sekretarka".
→ Ответить
  • »
    »
    10 лет назад, # ^ |
      Проголосовать: нравится +13 Проголосовать: не нравится

    But problem 2 can be solved on a single computer, there is probabilistic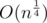 algo

    → Ответить
    • »
      »
      »
      10 лет назад, # ^ |
        Проголосовать: нравится +3 Проголосовать: не нравится

      By the way, I always wonder why people don't multiply the complexity by log(n) which goes from finding gcd on every step? Let alone multiplying it once again when we work with big numbers and every operation consumes not constant, but logarithmic amount of time.

      → Ответить
      • »
        »
        »
        »
        10 лет назад, # ^ |
          Проголосовать: нравится 0 Проголосовать: не нравится

        Because on average gcd will not really be log, and with sensible limits big numbers is just a constant

        → Ответить
        • »
          »
          »
          »
          »
          10 лет назад, # ^ |
            Проголосовать: нравится +8 Проголосовать: не нравится

          Because on average gcd will not really be log

          How to prove it? If I got you right, you say that there is an upper bound for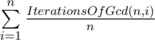 that is better than log(n).

          → Ответить
          • »
            »
            »
            »
            »
            »
            10 лет назад, # ^ |
              Проголосовать: нравится 0 Проголосовать: не нравится

            It's indeed O(log(n)) number of steps on average. About Pollard's rho algorithm, probably textbooks usually mention only expected number of iterations to avoid analyzing complexity for different arithmetic operations implementations.

            → Ответить
            • »
              »
              »
              »
              »
              »
              »
              10 лет назад, # ^ |
                Проголосовать: нравится 0 Проголосовать: не нравится

              Thank you for the link!

              Yeah, your claim is correct for elimination of the second log(n), but after reading the wiki article I still have no idea why they don't mention the first one in the expected complexity.

              → Ответить
    • »
      »
      »
      10 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится
      • Yeah , that means it is very unlikely to appear in the contest, and same for problems having such an algo . — I just mentioned it because it is a simple example which conveys the idea of this contest ,that is, Speeding up Using Multiple Instances
      • So if that does not count as problem 2 . Here is another one .
        Problem
        Given a sequence of N(<=10^10) integers , find if there exists a Majority element.
        Idea
        Divide sequence into say K segments , then we process each of them individually to find candidates of Majority element and then the Majority element itself , if any .
        So Complexity reduces to O( N / k )
      → Ответить