Hi, In this problem, I am using the idea that AM >= GM just like in the editorial but with slightly different steps.
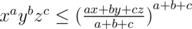
Equality should hold when all elements are equal. So according to me, x = y = z and the solution I arrive at is that x = y = z = S / 3
But this is incorrect as seen from the test case
S = 10
a = 1, b = 6, c = 3
My solution gives x = y = z = 3.33 and hence xa·yb·zc = 169350.87
But the optimal solution is x = 1.0, y = 6.0, z = 3.0 with xa·yb·zc = 1259712
What is the flaw in my math? Is this not a correct way to use GM <= AM? I don't understand why my solution differs from the solution given in the editorial even though the principle behind both is the same.











why equal?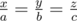
But for AM=GM inequality to hold shouldn't all elements be equal? So ax+by+cz means a x's b y's and c z's should all be equal right?
http://www.artofproblemsolving.com/wiki/index.php/AM-GM says: "The equality condition of this inequality states that the arithmetic mean and geometric mean are equal if and only if all members of the set are equal"
As far as I understood, you have to solve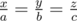 with x + y + z = S, where a, b, c, S is given.
with x + y + z = S, where a, b, c, S is given.
But for AM=GM inequality to hold shouldn't all elements be equal? So ax+by+cz means a x's b y's and c z's should all be equal right?
You wrote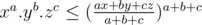 which is true and that equality will hold at x = y = z which is also true but there is no fixed value for the right hand side so it may be better for you to be less than a huge value than equal to a smaller one.
which is true and that equality will hold at x = y = z which is also true but there is no fixed value for the right hand side so it may be better for you to be less than a huge value than equal to a smaller one.
This is why we go according to this method
therefore,
I would have gone on but I am tired of manipulating LaTex symbols.
Some manipulation should show you that the term we want to maximize is now bounded above by a constant value (this is where the difference is between what your solution and authors solution) so you know that you can only get to that constant when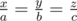 and x + y + z = S.
and x + y + z = S.
Why is it an issue if there is no fixed value on the right hand side? Also if x+y+z <= S then it has to be bounded right?
Look at the example you have given.
For the solution you find (x=y=z=3.33) lhs = rhs, but for the optimum solution(x=1,y=6,z=3) lhs < rhs.
What I am saying is that if your rhs is extremely huge and your lhs is slightly smaller than it then that is better than having a small rhs and an equal lhs.
Hence, you want a constant rhs so that you know that the term you are maximizing can never do better than that.
Aahhhhh... I get it. So I found the condition for equality of AM and GM but that is not the condition for upper bound of GM?
From what I understand you have manipulated to use AM >= GM in such a way that the AM is the upper bound and equality also guarantees optimality. Am I right?
Exactly.
Thanks a ton! Spent 5 hours on this!
Why should GM give maximum when you use it that way?
You have found an inequality which gives a constant upper bound for the GM. Now you know the conditions for which you can achieve equality. You use those conditions to maximize GM.
I would prefer it if someone more experienced than me would verify my approach but I can't see any reason as of now for it to be wrong.
I found out for 2 dimension why x/a = y/b gives maximum.
I am assuming NO z at all so eq. is (x^a)*(y^b) and x+y=S x=S-y so the eqn. becomes ((S-y)^a)*(y^b)
for max. we derive w.r.t y and equate to 0 i.e -a*(S-y)^(a-1)*(y^b) + b*(y^(b-1))*(S-y)^a = 0 solving we get (S-y)*b — a*y =0 => b*x=a*y => x/a=y/b i.e if x/a=y/b the eq. will be a maximum or minimum (Double derive and check i think it will be maximum)
I have no idea how to do for 3d i.e with z included