Suppose you have a triangle(x1,y1,x2,y2,x3,y3) and another one (x11,y11,x22,y22,x33,y33) . Coordinates don't come in a specific order.
The question: Can you draw the second triangle by just moving or rotating the first one? You can't detach the triangle from the board. EX: Therefore, using any of this two triangles you can't draw the other one. 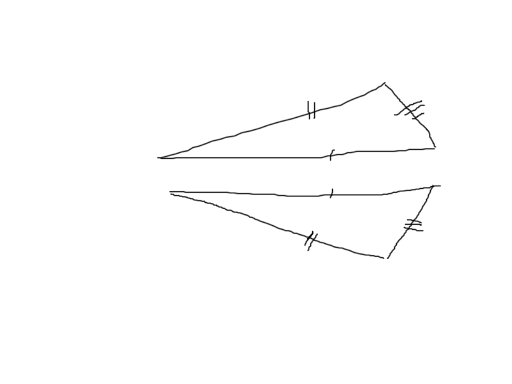
So, one way is to compare the area and the angles, but still can't figure out how to deal with the case given above (where the area and the angles are equal, but the answer is still "NO". Maybe it's a special use of signed area formula?
UPD!!! Thanks everyone! Here's how I solved it.
Read coords of the first triangle
Compute d1 (between point 1 and 2), d2 (2-3), d3 (1-3).
Put them in a separate vector. (We suppose that the direction is clockwise)
Compute the signed area, if it's less than zero, swap vector[0] with vector[2]. (we took the wrong direction, switch to counter-clockwise).
Repeat 1-2-3-4 for the second triangle.
Compare all the shifts (either to left or right) of the first vector with the second vector (to check for matches). If it matches — the answer is YES and NO otherwise.











Can you provide the link to the problem, one possible solution is to compare length of sides of triangles and area of triangles.
On the image above you can see that the lengths and areas are equal, but the answer is still "NO". I could, but this is a russian OJ and it requires registration, sorry. Here
I think you can indeed compare the sides, but make sure you use the same ordering (clockwise vs. counter clockwise) for both triangles. For example, given your picture, and supposing the length of the side is the number of lines you drew on it, the possible clockwise orderings for the first triangle are: (1, 2, 3), (2, 3, 1), (3, 1, 2). The clockwise orderings for the other triangle are: (1, 3, 2), (3, 2, 1), (2, 1, 3), so there are no matches between the first triangle's orderings and the second triangle's orderings, thus the answer is "NO".
Thanks, that clears things a bit. By the way, in geometry class we used to mark equal sides this way ( the same number of lines means equallity between the segments ).