Даны два треугольника (координаты трех точек) . Координаты не идут в какой-то особой последовательности.
Вопрос Можно ли нарисовать второй треугольник, используя как шаблон первый? При это треугольник не разрешается отрывать от доски, но можно крутить и перемещать.
EX: Вот пример, в котором ответ будет "НЕТ", ибо треугольник нужно сначала оторвать от доски, перевернуть, а потом вернуть на доску.
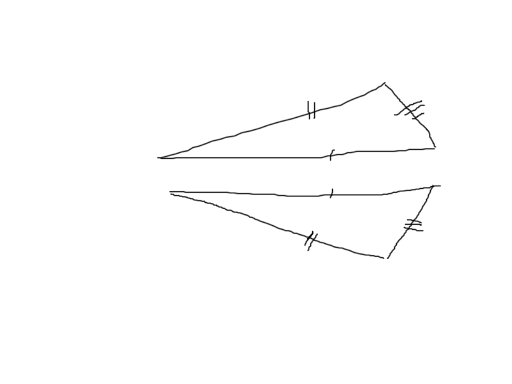
Сравнивать площадь и углы мало (пример выше тому доказательство), может нужно как-то по-особенному использовать ориентированную площадь?
UPD!!! Решение такое.
Читаем координаты первого треугольника
Вычисляем d1 (расстояние между 1 точкой и 2), d2 ( 2-3 ), d3 (1-3).
Вставляем в вектор эти расстояния (предполагаем, что порядок точек по часовой стрелке)
Вычисляем ориентированную площадь, если она меньше нуля, мы ошиблись, порядок против часовой, так что меняем местами vector[0] и vector[2].
Делаем тоже самое для второго треугольника.
Перебираем все сдвиги первого вектора на равенство со вторым (если находим равенство — ответ "ДА"), если равенство не нашли — "НЕТ".










Порядок длин сторон по часовой или против должен быть одинаковый. Если хочется, то можно воспользоваться ориентированной площадью :)
Как именно? 1 1 1 2 2 1 — Площадь 1
2 1 2 2 1 2 — Площадь -1.
Но ответ — "ДА".
Ну уж не садись на плечи, подумай сам =)
Давыше предложили гораздо более простое решение...
Can you provide the link to the problem, one possible solution is to compare length of sides of triangles and area of triangles.
On the image above you can see that the lengths and areas are equal, but the answer is still "NO". I could, but this is a russian OJ and it requires registration, sorry. Here
I think you can indeed compare the sides, but make sure you use the same ordering (clockwise vs. counter clockwise) for both triangles. For example, given your picture, and supposing the length of the side is the number of lines you drew on it, the possible clockwise orderings for the first triangle are: (1, 2, 3), (2, 3, 1), (3, 1, 2). The clockwise orderings for the other triangle are: (1, 3, 2), (3, 2, 1), (2, 1, 3), so there are no matches between the first triangle's orderings and the second triangle's orderings, thus the answer is "NO".
Thanks, that clears things a bit. By the way, in geometry class we used to mark equal sides this way ( the same number of lines means equallity between the segments ).