Третий раунд завершился.
Как решаются B и E?
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Третий раунд завершился.
Как решаются B и E?
| Название |
|---|



в Б. посортим массив B. потом динамика dp[i][lf][rg][k] — макс ко-во очков если мы поставили i первых чисел из A, lf наименьших и rg наибольших чисел из B, k = 0..1 — последнее число перевернуто или нет.
E: заметим, что фишки могут занимать всего n = 21 различную позицию, а также то, что самая правая из фишек никогда не движется влево. Состояния будем записывать как (i, j), где 0 ≤ i ≤ j < n.
Тогда просуммируем (по линейности матожидания сумма будет ответом) такие величины: — ожидаемое число ходов до попадания из (0, 0) в (0, 1), а также для i от 2 до n — ожидаемое количество ходов до попадания из (i - 2, i - 1) в (i - 1, i) (легко заметить, что через любое из этих состояний надо пройти).
— ожидаемое число ходов до попадания из (0, 0) в (0, 1), а также для i от 2 до n — ожидаемое количество ходов до попадания из (i - 2, i - 1) в (i - 1, i) (легко заметить, что через любое из этих состояний надо пройти).
Заметим, что в каждом конкретном слагаемом можно считать одну фишку неподвижной, а другую движущейся, что даёт систему из i уравнений на i переменных: xk — матожидание времени попадания из (k, i - 1) в (i - 1, i) 0 ≤ k ≤ i - 1. Для них можно составить уравнения вида xk - p·xmax(k - 2, 0) - (1 - p)·xk + 1 = 1, где xi положим равным 0. Нужно найти xi - 2. Для этого решим систему Гауссом.
Итого, находим n слагаемых, каждое за O(n3), итого O(tn4).
А можно просто решить за t * n^6 Гауссом
B: M фишков есть отсортированных; между два из N фишков не нужно дать более одного из M фишков. Динамическое программование: dp[x][i][j][k] = первых j и последних k из M фишков добавленных пред i-й из N (который есть перевёрнут — x = 1, или нет — x = 0). Кроме стандартных транзиций (dp[0][i][j][k] = max(dp[0][i - 1][j][k], dp[1][i - 1][j][k]), dp[1][i][j][k] = dp[0][i - 1][j][k] + F[i]) можно добавить максимальную фишку между i и i - 1 (или пред i = 1) и перевернуть ее (dp[0][i][j][k] не меньшее dp[0][i - 1][j][k + 1] + P[k]) или минимальную и не перевернуть (dp[1][i][j][k] не меньшее dp[1][i - 1][j + 1][k] + F[i]). Если остаются фишки из M, даем их за N-ю жадным алгоритмом. Сложность: O(NM2).
Screencast
Как решать F?
Как С решается?
Опытным путём выяснилось, что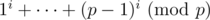 равняется 0, если i не делится на p - 1, и p - 1 иначе. Наверняка как-то красиво доказывается.
равняется 0, если i не делится на p - 1, и p - 1 иначе. Наверняка как-то красиво доказывается.
Таким образом, решение:
Почему ответ такой для i = k(p - 1), очевидно из малой теоремы Ферма.
Я умею понимать, почему получается ноль, для нечётных i (при p > 2):
12k + 1 + ... + (p - 1)2k + 1 = 12k + 1 + 22k + 1 + ... + ( - 2)2k + 1 + ( - 1)2k + 1 = = 12k + 1 - 12k + 1 + 22k + 1 - 22k + 1 + ... = 0.
Про общий случай тоже интересно было бы услышать.
Пусть x — первообразный корень по модулю p. Тогда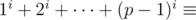
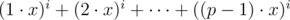

 . А так как
. А так как 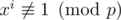 при
при 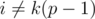 , то
, то 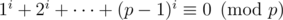
А кто-нибудь знает, где Series standings можно посмотреть, а то на самом снарке результаты от предыдущей серии?