Adiv2

Для решения задачи будем хранить два массива hused[j] и vused[j] размера n, изначально заполненных false. Будем обрабатывать перекрестки в списке от 1-го к n-му, и если для i-го перекрестка оба значения hused[h_i] и vused[v_i] равны false , i-ый день нужно добавить к ответу и установить значения hused[h_i] и vused[v_i] в true, означающих, что h_i-ая горизонтальная и v_i-ая вертикальная теперь заасфальтирована, а в противном случае нужно просто пропустить очередной перекресток.

Такое решение работает за O(n²).

Авторское решение: 13390628

Bdiv2

Чтобы получить оптимальный ответ, роботу нужно двигаться от первого компьютера к последнему, затем от последнего к первому, потом опять от первого к последнему, и т.д., попутно собирая те части информации, которые он может собрать на момент нахождения рядом с компьютером. Таким образом робот будет по максимуму использовать ресурсы, затраченные на смену направления движения. Несмотря на наличие более быстрых решений, от участников требовалось лишь решение с асимптотикой O(n²).

Авторское решение: 13390612

Adiv1

Пусть ответ представляет собой массив a₁ ≤ a₂ ≤ ... ≤ a_n. Далее будем пользоваться тем, что gcd(a_i, a_j) ≤ a_min(i, j).

Верно, что gcd(a_n, a_n) = a_n ≥ a_i ≥ gcd(a_i, a_j) для любых 1 ≤ i, j ≤ n. Это значит, что a_n равен максимальному элементу таблицы. Запишем в ответ a_n максимальный ответ и удалим его из текущего набора элементов. После удаления gcd(a_n, a_n) в наборе будут содержаться gcd(a_i, a_j) для любых 1 ≤ i, j ≤ n, таких, что 1 ≤ min(i, j) ≤ n - 1.

Из последних двух неравенств следует, что gcd(a_i, a_j) ≤ a_min(i, j) ≤ a_n - 1 = gcd(a_n - 1, a_n - 1). Поскольку в наборе содержится gcd(a_n - 1, a_n - 1), максимальный элемент в наборе равен a_n - 1. Поскольку a_n уже известен, удалим из набора gcd(a_n - 1, a_n - 1), gcd(a_n - 1, a_n), gcd(a_n, a_n - 1) . Теперь в наборе содержатся gcd(a_i, a_j), для любых 1 ≤ i, j ≤ n таких, что 1 ≤ min(i, j) ≤ n - 2.

Далее повторим это операцию для каждого k from n - 2 to 1, устанавливая a_k равным максимальному элементу в оставшемся наборе и удаляя gcd(a_k, a_k), gcd(a_i, a_k), gcd(a_k, a_i) для всех k < i ≤ n из набора.

С помощью математической индукции нетрудно доказать корректность такого алгоритма. Чтобы быстро выполнять удаление и получение максимального элемента в наборе, можно использовать, например, структуры map или set, что позволит реализовать решение с асимптотикой .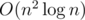

Авторское решение: 13390679

Bdiv1

Можно посчитать матрицу размера n × n mt[i][j] — длина наибольшей неубывающей подпоследовательности в массиве a₁, a₂, ..., a_n, начинающейся с элемента, не меньшего a_i и заканчивающейся непосредственно в элементе a_j.

Теперь, если мы имеем две матрицы размера n × n A[i][j] (ответ для массива a₁, a₂, ..., a_pn начинающегося с элемента, не меньшего a_i и заканчивающейся элементом a_j в последнем блоке массива (a_{(p - 1)n + 1}, ..., a_pn) и B[i][j] (ответ для массива a₁, a₂, ..., a_qn ), то произведение этих матриц

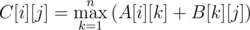
даст подобную матрицу, но для массива из p + q блоков. Так как такое произведение матриц является ассоциативным, воспользуемся быстрым возведением матрицы в степень для подсчета M[i][j] (ответ для массива a₁, a₂, ..., a_nT) — матрица mt[i][j] в степени T. Ответ на задачу — максимум матрицы M. Такое решение имеет асимптотику .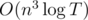

Авторское решение (с матрицами): 13390660

Существует альтернативное решение. Так как a₁, a₂, ..., a_nT содержит максимум n различных элементов, любая его неубывающая подпоследовательность содержит максимум n - 1 последовательных возрастающих соседних элементов. Пользуясь этим фактом, будем считать стандартное динамическое программирование на первых n блоках массива (a₁, ..., a_n²) и на n последних блоках массива (a_{nT - n + 1}, ..., a_nT). Все остальные блоки (а их T - 2n) между ними будут порождать равные элементы в результирующей неубывающей подпоследовательности.

Таким образом, для фиксированного a_i, в котором заканчивается неубывающая подпоследовательность длины p массива из первых n блоков, и для фиксированного a_j ≥ a_i, в котором аналогичная подпоследовательность длины s на последних n блоках массива начинается, нужно обновить ответ величиной p + (T - 2n)count(a_i) + s, где count(x) — количество вхождений x в массив a₁, ..., a_n. Получаем решение за .

Авторское решение ( с динамикой): 13390666

Cdiv1

Зафиксируем s и рассмотрим каждую пару (l, s). Тогда, если превосходящий подмассива содержит a_i, то a_i должен быть не меньше каждого a_j такого, что 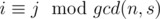. Будем использовать этот факт и решать задачу для фиксированного g = gcd(n, s) (g|n). Для последующей проверки того, что a_i может содержаться в превосходящем подмассиве, посчитаем для каждого 0 ≤ r < g

.

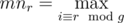Каждый периодический подмассив состоит из 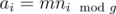и только из них. Для нахождения количества таких подмассивов будем пользоваться методом двух указателей и для каждого подходящего a_i такого, что 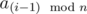не является подходящим, найдем такое a_j, что 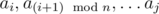являются подходящими и 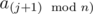не является подходящим. Пусть 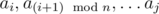представляет подотрезок из k элементов, т.е. 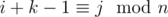. Любой подотрезок этого подотрезка так же является превосходящим, поэтому к отрезкам длины 1, 2, ..., k мы должны прибавить k, k - 1, ..., 1 соответственно. Так как сумма всех k не превосходит n, можно циклом увеличивать нужные значения. Случай, когда все a_i являются подходящими, нужно обрабатывать отдельно. После подсчета всех необходимых величин, мы должны добавить лишь те количества подотрезков длины x, для которых gcd(x, n) = g.

Описанное решение имеет асимптотику O(d(n)n), где d(n) — количество делителей n.

Авторское решение: 13390645

Ddiv1

Известно, что для простого p и натурального n максимальное α такое, что p^α|n!, вычисляется по формуле 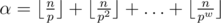, где p^w ≤ n < p^w + 1. Так как 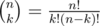, максимальное α для 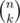вычисляется по формуле .

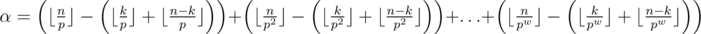Примечательно, что если представить n, k и n - k в p-ичной системе счисления, деление числа с округлением вниз на p^x соответствует отбрасыванию последних x цифр в его p-ичном представлении. Поскольку k + (n - k) = n, i-ое слагаемое в формуле для α соответствует величине переноса разряда с i - 1-ой к i-ой цифре в сложении k и n - k в p-ичной системе счисления и может принимать значения ноль или один.

Переведем A в p-ичную систему счисления и будем далее работать только с этим его представлением. В случае, если α превышает количество цифр в представлении A то, как описано выше, ответ равен 0. Далее будем считать динамическое программирование на представлении числа A.

dp[i][x][e][r] — ответ, если мы рассмотрели первые i цифр числа n и k, при этом эти цифры в n могут равняться первым цифрам A (булева e), x-ая степень p уже была набрана, и величина переноса с текущего в следующий разряд равна r . Переходы будем осуществлять вперед, имея, таким образом, не более p² вариантов расстановки цифр в n и k. Поскольку перебор всех таких вариантов невозможен, нужно заметить, что для перехода в фиксированное состояние (его первый параметр равен i + 1) количество вариантов расстановки цифр равняется сумме арифметической прогрессии, поэтому переход с помощью умножения на сумму прогрессии можно осуществлять за O(1).

Крайне рекомендуется ознакомиться с авторским решением за O(|A|² + |A|min(|A|, α)).

Авторское решение: 13390698

Ediv1

Количество бинарных функций на 4 переменных равняется 2²⁴, и каждую из них можно закодировать двоичным числом из 2⁴ бит , где значение каждого бита соответствует значению функций в наборе переменных, соответствующему номеру бита. Верно, что если mask_f и mask_g соответствуют функциям f(A, B, C, D) и g(A, B, C, D), то функции (f|g)(A, B, C, D) соответствует mask_f|mask_g bitmask.

Построим бинарное дерево разбора выражения. Замечу, что количество нелистовых вершин в нем равно 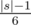. Будем считать динамическое программирование для каждой вершины v дерева разбора — dp[v][mask] равно количеству способов вставить символы в выражение, образованное поддеревом вершины v так, чтобы оно соответствовало функции, задающейся маской mask. Для листовых вершин значения динамики вычисляются ``в лоб'' перебором каждой из 16 функций и подстановкой переменной в функцию. Для нелистовых вершин существует способ перебирать все пары варинтов функций в сыновьях за 4¹⁶: dp[v][lmask|rmask] +  = dp[l][lmask] * dp[r][rmask].

Однако вся задача в том, чтобы делать это быстрее. Давайте посчитаем s[mask], где s[mask] равняется сумме ответов динамики для всех подмасок mask (submask&mask = submask) за 2⁴·2²⁴ операций с помощью следующего кода:

for (int mask = 0; mask < (1 << 16); ++mask) s[mask] = dp[x][mask];
for (int i = 0; i < 16; ++i)
    for (int mask = 0; mask < (1 << 16); ++mask)
        if (!(mask & (1 << i))) s[mask ^ (1 << i)] += s[mask];

Посчитаем sl[mask] и sr[mask] для dp[l][mask] и dp[r][mask] соответственно. Если приравнять s[mask] = sl[mask] * sr[mask], s[mask] будет хранить сумму произведений пар значений масок левого и правого сына, таких, что обе эти маски являются подмасками mask. Так как нам нужны пары, побитовый OR которых даст ровно mask, нужно исключить пары, побитовый OR которых дает подмаску mask, не равную mask. Для этого будем пользоваться формулой включений-исключений:

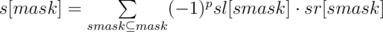, где p равно количеству единичных бит в mask^submask.

Такую сумму можно посчитать аналогичному выше образом, но используя вычитание вместо сложения:

for (int mask = 0; mask < (1 << 16); ++mask) s[mask] = sl[mask] * sr[mask];
for (int i = 0; i < 16; ++i)
    for (int mask = 0; mask < (1 << 16); ++mask)
        if (!(mask & (1 << i))) s[mask ^ (1 << i)] -= s[mask];

Таким образом можно пересчитывать значения динамики в вершине за 3·2⁴·2¹⁶ операций.

Авторское решение: 13390713