Сейчас пишу статью на wiki — конспекты про битовые операции, трюки и прочую битовую магию. Если вы знаете полезные трюки с битами, которые применяются в алгоритмах, а также просто прикольные вещи, то делитесь своими трюками в комментариях. Также приветствуются извращённые решения известных задач. Например: обменять значения переменных, не использую третью переменную с помощью XOR.
Приветствуются комментарии в виде:
- Описание задачи
- Решение задачи в виде кода, по-возможности короткое объяснение для не очевидных трюков.
Пример идеального комментария:
Является ли число степенью двойки?
unsigned int v; // we want to see if v is a power of 2
bool f; // the result goes here
f = v && !(v & (v - 1))
Короткое объяснение: Пусть v — это степень двойки (в двоичном представлении 1 единица и k нулей справа), тогда v — 1 в двоичном представлении это число, состоящее из k единиц. Очевидно, что побитовое И чисел
v и v — 1 должно давать в результате 0.
Задача для затравки: Найти младший единичный бит за O(1)
UPD: Интересные ссылки из комментов










Младший единичный бит так вроде?
((a^(a-1))+1)>>1
Вариант покрасивее:
(a^(a-1))&a
Ещё можно так:
i & -i.Проверка неполна: надо еще проверить, что v ≠ 0. Более того, стоит отдельно указать, что происходит в знаковых переменных (например, иногда — undefined behavior на плюсах).
Только не надо, пожалауйста, учить людей undefined behavior без указания того, к чему это может привести (aka писать "в одну клёвую команду").
По делу (если что-то из этого вам непонятно, могу расписать):
~, не!), пересечение (&и&=), объединение (|,|=), установка бита по номеру (| 1 << x), снятие бита по номеру (& ~(1 << x)), сдвиги влево-вправо (стоит сделать замечание про знаковость в плюсах и про>>>в Java).__builtin_popcount,__builtin_ctz,__builtin_clzи прочая, прочая, прочая (в том числе с суффиксамиll).(a >> x) & 1иa & (1 << x), чем отличаются. Если в плюсах писать внутри условия if, то ничем. А вот если пытаться немедленно использовать результат операции внутри другой, то возможны варианты: первая штука возвращает 0/1, а вторая — 0/x-ый бит, в разных местах нужно разное.std::bitset^и<<в плюсах по сравнению с некоторыми другими операциями (например, сравнениями или сложениями).Еще можно загуглить и получить вот это. Пара вещей оттуда (не проверял):
(x ^ y) < 0.(v * 0x200040008001ULL & 0x111111111111111ULL) % 0xf;WOW! Очень круто.
Спасибо, уже добавил в избранное :).
Распишите, пожалуйста, 7, 8, 9 и 12 (КАК оно работает o_O?)
UPD yeputons и vogel, спасибо, теперь понятно!
7) Просто тебе нужно узнать в маске a бит под номером x. Ты сдвигаешь единицу на x бит влево и & с маской или можно сдвинуть маску на x бит вправо и & с 1.
Именно. В плюсах, например, в некоторых случаях неважно (в Java аналогично, но надо дописать
!= 0):А вот в некоторых — важно, какой бит мы получаем:
Некоторые путаются.
Про 8: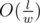 (тут l — размер маски, w — длина машинного слова, т.е. 32/64). Например:
(тут l — размер маски, w — длина машинного слова, т.е. 32/64). Например:
std::bitsetявляется длинной битовой маской фиксированного (на стадии компиляции) размера. С ней можно делать разные операции заАлгоритмы, которые сводятся к каким-то простым операциям с длинными масками (побитовое "или", скалярное произведение и прочее), этой штукой оптимизируются. Алгоритм Флоида (имелся ввиду для подсчёта достижимости, а не расстояний):
12 расписано, например, тут, тут и тут (гуглится по запросу "fast inverse square root"). Кратко: магическая константа нужна лишь для хорошего первого приближения, дальше используется одна итерация метода Ньютона, которая уточнает результат. Магическая константа пользуется тем, что в вещественных числах отдельно хранятся мантисса и экспонента, а в качестве первого приближения корня можно просто поделить экспоненту пополам и сменить у неё знак. По ссылкам более подробно рассказывается, почему константа именно такая (по второй ссылке — какие еще бывают, например, для кубических корней).
9: Сложение за O(w). Для знаковых тоже сработает (просто потому что знаковые числа хранятся как соответствующие вычеты в кольце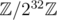 , поэтому сложению неважен знак), но на плюсах переполнение в знаковых типпах — undefined behavior, что нехорошо.
, поэтому сложению неважен знак), но на плюсах переполнение в знаковых типпах — undefined behavior, что нехорошо.
Время работы такое, потому что в худшем случае у нас будет один-единственный перенос, который мы будем протаскивать по всему числу, например, (2k - 1) + 1.
За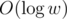 описано либо на вики, либо можно так: сначала посчитаем, в какие разряды будут переносы (при нормальном сложении с учётом всех переносов), а потом за одну операцию проксорим исходные два числа и переносы.
описано либо на вики, либо можно так: сначала посчитаем, в какие разряды будут переносы (при нормальном сложении с учётом всех переносов), а потом за одну операцию проксорим исходные два числа и переносы.
Перенос в разряд i случается, если сумма кусков чисел, составленных из всех битов до i-го (исключительно) не меньше 2i. Это что-то сложное, давайте лучше научимся быстро сравнивать начала двух чисел на "больше" и "меньше либо равно":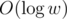 ), возможно, я наврал, что это делается для битовых операций — надо подумать.
), возможно, я наврал, что это делается для битовых операций — надо подумать.
aи~b. Здесь~b— это максимальное такое число, что ни на каком префиксе при сложении сbпереносов нет. Соответственно, если какой-то префиксaбольше соответствующего префиксаb, возникнет перенос. А сравнивать мы умеем деревом отрезков. Для схем это делается совсем просто (за глубинуВ Java нет операции <<<
Действительно, спасибо. Написал по аналогии. Интересно, что бы она могла делать.
Поищи книгу Алгоритмические трюки для программистов, там полно трюков с битовыми операциями.
Да-да, знаю про неё. Но хочется посмотреть на именно те трюки, которые люди используют.
По множеству масок посчитать все маски, которые содержат хотя бы одну из них:
Смысл состоит в том, что мы храним по 25 значений динамики "удовлетворяет ли названному условию?" в каждом элементе массива, таким образом биты int-ов соответствуют последним 5 битам маски, номер в массиве оставшимся битам. Переходы по "внешним" битам тривиальны, а по "внутренним" выражаются с помощью битовых операций.
P. S. Константы в двоичной записи выглядят так: 00000000000000001111111111111111, 00000000111111110000000011111111, 00001111000011110000111100001111, 00110011001100110011001100110011, 01010101010101010101010101010101, то есть мы выделяем среди наших состояний те, в которых нет 4-го, 3-его, 2-го, 1-го, 0-го битов и делаем из них соответствующие переходы.
Zero is not a power of two. Your code says otherwise :)
Yeah.
232 = 0
Я верю в то, что битовые трюки за меня делает -O2 :)
Например, https://en.wikipedia.org/wiki/Hamming_weight
Если что, пункт 9 из списка Егора уже есть в вики-конспектах. Правда, на мой вкус, там не слишком понятное описание.
Минимум среди (x, y) = y ^ ((x ^ y) & -(x < y))
Когда x<y: y ^ ((x ^ y) & -(x < y)) = y ^ ((x ^ y) & -1) = y ^ (x ^ y) = x
Когда x>y: y ^ ((x ^ y) & -(x < y)) = y ^ ((x ^ y) & 0) = y ^ 0 = y
or:
f = __builtin_popcount(v) == 1;
This method is much slower.
Всё написано до нас: link
Да, оттуда я взял большую часть трюков, но хотелось услышать трюки именно от олимпиадников с опытом.
Smallest bit set to 1 of an integer
Explanation: -number representation using 2-complement keeps the smallest 1-bit and inverts the other most significative bits.
Unsetting the smallest 1-bit of an integer
int number = 123; number -= number & -number;
Counting the number of bits set to 1
Toggle bit i from 1->0 or 0->1
Xor with bit set to 1, makes it change its value, whereas the other bits are 0 and don't change anything.
Iterate all subsets of a bitmask in increasing order
Iterate all subsets of a bitmask in decreasing order
Can u plz give a small example for "Iterate all subsets of a bitmask in increasing order". It is not clear to me... :/
Один из классических рюкзаков, а точнее Subset sum problem, на битсетах:
И работает быстро, и пишется просто.
Очень круто, спасибо
Оставлю тут pdf
Из того, о чём ещё не писали, там, например, есть рюкзак с восстановлением ответа и Гаусс.
А номер младшего за O(1) умеешь? ;)
Я умею с таблицей предподсчёта, взяв число по модулю 37. Работает для 32-битных чисел. Для 64-битных нужно 67. Забегая вперёд -- для __int128 достаточно 131 :)
Да, я это и имел в виду =)
Таблицу можно сократить! :)
http://supertech.csail.mit.edu/papers/debruijn.pdf
Выбирайте:
Swap two integers
Check whether two integers are equal or not:
Check if a equals -1 or not
Get the largest number I can!
For the least number
Operation x & (x — 1) sets rightmost 1 to 0. As powers of 2 have only one 1 — it can be used to check them.
My favorite is binary searching by bit manipulation — no off-by-1 errors!
Original source: https://github.com/pathikrit/scalgos/tree/master/src/main/scala/com/github/pathikrit/scalgos
Could you explain please what
Seq(p, n) find fmeans?pandnare numbers in[0, Long.MaxValue]and[Long.MinValue, 0]respectively for which f maybe satisfactory.Seq(p, n)creates a sequence of these 2 numbers andSeq(p, n) find freturns the first one for which f is true else None. I am using Scala as my language; here's a Java/C++-ish version (not tested):Дико прошу прощения, если мой коммент покажется неконструктивным, но опасаюсь, как бы вся Ваша статься не получилась ещё более неконструктивной.
Такие вещи позволительно писать только когда есть чёткое описание возможных подвохов. Хотя бы тот же классический обмен двух переменных без третьей — по моему глубокому убеждению, надо либо обязательно указывать, что оно работает только при
&x!=&y(а при&x==&yприводит к утрате значения этой переменной), либо вообще не рассказывать о таком! И это касается не только конкретно обмена, а вообще всего.Да, спасибо, постараюсь это учесть. Казалось бы из всех трюков только 3 — 4 вызывают опасения.
Can someone provide links to the problems, where you need a fast way to count number of 1's in mask or index of last setted bit?
633G - Yash And Trees