Сначала в общих чертах о раунде.
Моими задачами в этом раунде были задачи A-div2, B-div2, C-div2/A-div1, E-div2/C-div1, D-div1. Сначала я хотел провести на них контест исключительно для второго дивизиона. Однако затем мы решили провести общий раунд. MikeMirzayanov подготовил задачу про молоко, anonymous предоставил задачу E-div1. Кроме того, по напутствию RAD были усложнены Аземблер и Флаги.
По-моему, получилось неплохо для первого раза (кроме небольшого фейла с рамочками). Во всяком случае, мне понравилось. Правда, я не ожидал, что Аземблер и Флаги решит так мало народу.
А теперь разбор.
Задача A (div.2) - Восстановление пароля
Текст задачки был актуален чуть более года назад, когда свирепствовал вирус piggy.exe :) Но в то время у меня не было возможности где-либо опубликовать эту задачу.
Вот пример решения: http://pastebin.com/hMV0NcjN
Задача B (div.2) - Друзья
Возможно, некоторых смутила формулировка утверждения. Однако именно так оно звучит в книжке, из которой я его нагло скопировал :)
Т.к. вершин в графе всего 5, достаточно написать 3 вложенных цикла for (каждый цикл соответствует одной вершине графа) и проверить, что ребра между этими вершинами имеют одинаковый цвет.
Пример решения: http://pastebin.com/gswaxGmM
На самом деле ответ FAIL будет лишь в одном случае - когда в графе ровно 5 ребер и они образуют цикл длины 5 (как в тесте 2). Вот шуточное решение на эту тему: http://pastebin.com/09T0ixrJ
Задача A (div.1) / C (div.2) - Рамочки
Итак, давайте разберемся в задаче. Во-первых, заметим, что ответ всегда не превосходит 3, т.к. любое множество подряд идущих папок можно разбить на 3 прямоугольника (возможно, пустых). В первый прямоугольник мы поместим конец первой строки, во второй - все, кроме конца первой строки и начала последней (это будет прямоугольник с шириной m), а в третий - начало последней строки.
Самый простой способ решить задачу --- проверить, что ответ 1 или 2, а иначе вывести 3. Давайте рассмотрим, в каких случаях ответ меньше 3.
Итак, пусть ответ - единица. Значит, все требуемые папки можно выделить за одно движение мышкой. Вот эти случаи (в скобках показан тест для этого случая):
- первая и последняя папки находятся в одной и той же строчке (21 5 7 9);
- первая папка находится в самом левом столбце, а последняя - в самом правом (21 5 1 15), этот случай покрывает случай m = 1;
- первая папка находится в самом левом столбце, а последняя имеет номер n (21 5 6 21). Сюда же относится тот случай, когда надо выделить вообще все папки.
Теперь рассмотрим все случаи, когда ответ равен 2:
- первая и последняя папки находятся в соседних строчках (21 5 8 14);
- первая папка находится в самом левом столбце (21 5 6 13);
- последняя папка находится в самом правом столбце (21 5 4 15);
- последняя папка имеет номер n (21 5 4 21);
- столбец, в котором расположена первая папка, находится непосредственно справа от столбца, в котором расположена последняя папка (21 5 3 12). Мне кажется, это самый хитрый случай в задаче.
Если ни одно из этих условий не выполняется, то ответ равен 3.
Пример решения: http://pastebin.com/8QRytzzF
Еще эту задачу можно было писать сжатием координат и перебором, но психов среди нас нет :)
Задача B (div.1) / D (div.2) - Окончание сессии
Задача решается жадным алгоритмом. Нужно последовательно пробовать переливать из каждой бутылки молоко в любую кружку, которая для этого подойдет и в максимально возможном количестве.
В ходе процесса надо помнить, сколько молока находится в каждой кружке и каждой бутылке, а также из каких бутылок наливали в каждую кружку и куда переливали из каждой бутылки. Эта информация нужна, чтобы определять, а можно ли перелить из конкретной бутылки в конкретную кружку или нет.
Остается это просто написать - ничего сложного, как мне кажется. Единственный момент - сравнивать вещественные числа надо, используя EPS. Без этого можно получить WA на тесте 12 (50 1000 49), где из-за неправильного сравнения программы некоторых участников выдавали NO, тогда как решение существует.
В обсуждении ниже показано, что ответ можно считать в целых числах, если взять объем бутылки, равный mn. А при выводе будем делить на mn и умножать на w. Ни одно из трех решений жюри до этого не додумались :)
Пример решения: http://pastebin.com/HG5Nrxne (оно уже не такое красивое, как предыдущие, но понять, как мне кажется, можно)
Задача C (div.1) / E (div.2) - Аземблер
Меня удивило маленькое количество сабмитов по этой задаче. Достаточно маленькие ограничения на n и большое ограничение по времени явно намекали на перебор. Кроме того, интуитивно понятно, что максимальный ответ находится в районе 5.
Для получения решения необходимо хранить (например, в векторе) текущие значения регистров и перебирать всевозможные новые значения, получаемые из текущих, а затем рекурсивно запускаться с новым набором чисел в регистрах. Попутно можно сохранять и саму программу.
Чтобы при этом не возникло TLE, надо хранить максимальную глубину рекурсии (собственно, это первое число в ответе), в которой мы достигли ответа, и не ходить глубже. Также не следует ходить в те состояния, где мы получаем число, большее n. Если же мы получили ровно число n, и наша глубина рекурсии меньше минимальной, запомним ответ и скопируем его в безопасное место, чтобы потом вывести.
Еще есть улучшение, которое состоит в том, чтобы перебирать числа по убыванию (так работает быстрее), но ограничения в 5 секунд хватало, чтоб перебирать числа как угодно.
Были и другие подходы к решению этой задачи: поиск в ширину и перебор для конкретного ответа.
Вот два решения: обычный перебор (http://pastebin.com/Z6ZF36st) и перебор для конкретного ответа (http://pastebin.com/viiYF9CB).
Задача D (div.1) - Флаги
Сначала я расскажу, как считать ответ для одного числа (т.е. L = R), а потом переделаю решение для общего случая. Дело в том, что изначально задумывалась как раз формулировка с конкретным числом полос N, и только потом мы было принято решение усложнить задачу. Мое решение не сильно оптимально (задачи все-таки не "фиолетовые", как оказалось, а некоторые решения - "фиолетовые" :) ). Я видел коды других участников, и у них все попроще.
Итак, задача для фиксированного N.
Обозначим за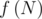 
число флагов с N полосами, считая симметричные флаги разными. Посмотрим, как, имея эту информацию, получить ответ на задачу.
На первый взгляд, достаточно поделить 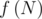на 2. Но, посмотрев повнимательнее, можно обнаружить, что это верно только для флагов, не являющихся палиндромами. Например, флаги-непалиндромы WBWB и BWBW симметричны, и надо учитывать только один из них --- здесь деление на 2 законно. А вот флаги-палиндромы, такие, как WBW, симметричны сами себе, поэтому деление на 2 для них приведет к ошибке.
Посмотрим, что можно сделать. Во-первых, заметим, что при четном N корректных флагов-палиндромов вообще не существует, т.к. иначе в центре встретились бы 2 полосы одного цвета, что невозможно, поэтому для четных N формула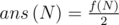 
верна.
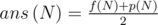, где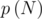 
--- количество флагов-палиндромов длины N. Но каждый флаг-палиндром нечетной длины N однозначно определяется своими первыми 
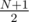полосами, и количество таких флагов-палиндромов равно 
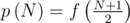(здесь, разумеется, симметрию учитывать не надо).Итак, мы свели нашу задачу к нахождению числа флагов с N полосами, причем симметричные флаги считаются различными. Заметим, что для того, чтобы пририсовать очередную полосу к флагу так, чтобы он остался корректным, нам необходимо знать лишь последнюю и предпоследнюю его полосы.
Применим динамическое программирование. В качестве состояния возьмем вектор
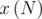из 8 чисел, каждая компонента которого будет содержать количество флагов c общим количеством полос N и определенными корректными последней и предпоследней полосами (как раз 8 вариантов). Сумма всех компонент этого вектора даст нам общее количество флагов с N полосами, т.е. 
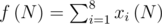.База динамики --- вектор
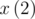, содержащий ровно 8 единиц (они соответствуют всем разрешенным парам цветов). Давайте подумаем, как можно найти вектор 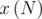, зная вектор 
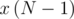.Оказывается, существует такая матрица A, что
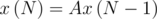. Элементы этой матрицы можно посчитать даже вручную, из следующих соображений. Например, пусть мы имеем комбинацию последних двух полос WB. Тогда можно справа дописать белую или желтую полосу, что будет соответствовать BW и BY. Поэтому в столбце матрицы, соответствующему WB, мы поставим единички в строках, соответствующих BW и BY. Все это займет не более минуты.И последний шаг. Очевидно, что
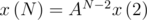. А возведение в степень можно проводить быстро, за логарифмическое время. Принцип в том, что, если N четное, то нам достаточно вычислить 
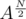и возвести эту матрицу в квадрат. А если N --- нечетное, то N - 1 - четное, и для степени N - 1 можно снова применить этот прием.Осталось не забыть, что при N = 1 все это неприменимо, зато можно сразу сказать, что ответ равен 4.
А теперь проапгрейдим это решение для случая отрезка
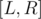.У меня есть два способа это сделать. Первый способ состоит в том, что в векторе состояний добавляется одна координата, а в матрице - новая строка и столбец. Эта новая координата в векторе состояний будет хранить сумму на отрезке
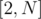(с L = 1 разберемся if-ом). Останется подогнать матрицу A, что делается довольно несложно. Попробуйте сами (подсказка: я умножал ее слева еще на одну, почти единичную матрицу).Второй способ мне понравился больше. Так же, как и ранее, разделим задачу на две: на палиндромы и непалиндромы. Научимся находить ответ для флагов без учета симметрии на отрезке
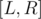. В вышеприведенных обозначениях ответ равен 
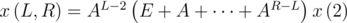. Покажем, как можно быстро и просто находить сумму E + A + ... + AN.Пусть b --- такая максимальная степень двойки, что 2b - 1 ≤ N. Разобьем нашу сумму следующим образом:
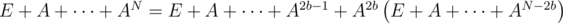.Оказывается, первая часть этого выражения легко считается:
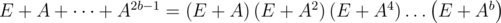. Вы можете сами убедиться в справедливости этого равенства. А сумма в скобках второй части выражения из предыдущего абзаца что-то напоминает... Разберетесь сами :)Ответ для палиндромов считается таким же способом. Будем полагать для удобства, что L и R - нечетные (если это не так, то к L можно прибавить единицу, а от R - отнять). Тогда
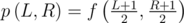.Вот и все. Остается не ошибиться, после каждой операции брать модуль и внимательно рассматривать крайние случаи.
Вот решение вторым способом: http://pastebin.com/wHu1tPgd
Наверное, можно все сделать куда проще. Пишите свои разборы, чем их больше - тем лучше!
Задача E (div.1) - Лостборн
Эта задача решается формулой включений и исключений. Только многие получили TLE, т.к. они почему-то не прогнали максимальный тест на своем компьютере (да, прогоняйте макс. тесты на своем компьютере!).
А остальные почувствовали, что что-то тут не так, и запоминали ответы для небольших N и конкретного ai в массив, чтобы в дальнейшем их не считать. Например, можно посмотреть решение победителя турнира rng_58, там все очень четко и понятно написано. Вот еще один пример такого решения: http://pastebin.com/4kcfJdAi
Более подробно об этой задаче написал ее автор anonymous вот в этом посте: http://mirror.codeforces.com/blog/entry/2216. У него есть решение, укладывающееся в ограничение по времени при N ≤ 1015, что, скорее всего, не сделало бы ни одно из решений, отправленных во время контеста. Это решение можно посмотреть в дорешивании.
(исправлено)
дфсбфс по значению двух элементов стека?upd. Уже осознал, что я не так понимаю.
Поддерживаю!
Именно это больше всего интересовало в разборе.
Набросок доказательства B div 1.
Пусть n < m, т.е. кружка меньше бутылки. Пусть кружки - вершины графа. Пусть каждая бутылка задает ребро графа (соединяет две кружки в которые из нее налито). Пусть на ребре, входящем в вершину, подписано, сколько в эту вершину наливается из соответствующей ребру бутылки, а текущий граф задает ответ задачи.
Пусть в этом графе есть некоторый цикл. Тогда k кружек получают все содержимое k бутылок, что невозможно.
Введем операцию проталкивания объема d по некоторому пути. Она будет заключаться в уменьшении для каждой бутылки на пути количества наливаемого на d в вершину, которая на пути раньше, и увеличения на d в вершину, которая позже. Это приводит к недоливу в первой вершине пути и переполнению в последней, причем можно выполнять эту операцию на объем вплоть до того, когда последняя бутылка пути будет полностью выливаться в последнюю вершину пути (внутри пути такого произойти не может, так как это автоматически означает переполнение вершины).
Пусть теперь у нас есть некоторый путь A->B. Протолкаем максимально возможное значение по этому пути. Получится, что в вершине А недолив, в В перелив, последняя бутылка пути целиком выливается в В. Перельем нужное количество молока из последней бутылки пути в А. Таким образом, для любого пути V1 -> V2 -> ... -> Vk мы можем убрать ребро Vk-1 -> Vk и добавить ребро Vk -> V1.
Этой операции достаточно, чтобы любой лес превратить в лес со степенью каждой вершины не больше 2, т.е. свести любой ответ к ответу, в котором наливание идет жадным способом.
Предложения по тому, как написать это яснее, принимаются.
2. На каждом ребре подписано два числа, сумма их равна объему бутылки.
Это означает, что некоторая бутылка пути полностью выливается в некоторую вершину, что автоматически означает переполнение этой вершины и тот факт, что эта вершина - последняя (проталкивание вызывает переполнение только одной вершины).
На самом деле, вдоль любого пути количество налитого из бутылки в более позднюю вершину пути убывает, это следует из утверждения "кружка меньше бутылки" и того факта, что все, что не налили в следующую вершину, наливается в эту.
Упростил, как мне кажется, доказательство, используя Вашу идею с графом. Очевидно что граф ацикличный, то есть разбит на деревья, в каждом дереве число ребер равно числу вершин минус 1, а количество деревьев равно k=m-n. Тогда составим уравнение для произвольной компоненты связности с числом вершин m0 и числом ребер n0: m0*w*n/m=(m0-1)*w. m0=n0+1, отсюда m0=m/k, а n0 = n/k, причем все компоненты одинаковы, значит нужно решить задачу хотя бы для одной. Заметим, что если мы не можем получить целочисленные m0 и n0, то задача решения не имеет. В противном случае задача для количества бутылок n0, которое на 1 меньше количества кружек m0 решается всегда очевидным образом (применить решение в целых числах).
При n >= m решение существует всегда
При n < m решение существует т. и т. т., когда n / gcd(m,n) + 1 == m / gcd(m,n)
Не читал разбор, посмотрел, что он очень длинный. Кажется, что для задачи, в которой надо посчитать какие-то матричные возведения в степень с какими-то уточнениями в разборе и правда много букав.
На контесте почти все возводили матрицы в степень.
At the beginning, v=0.
Bottle 1: v=0. Pour 3/4 into cup 1 and 1/4 into cup 2.
Bottle 2: v=1/4. Pour 2/4 into cup 2 and 2/4 into cup 3.
Bottle 3: v=2/4. Pour 1/4 into cup 3 and 3/4 (= 0) into cup 4.
It's similar if we pour 3/4 of 3 bottles into 3 cups and the rest 1/4 of 3 bottles into the other.
So, divide it into 2 progresses.
1. Make n cups full with n bottles. Each bottle remains the same volume of milk.
2. Make the other m-n cups full. So n%(m-n)=0 is the condition.
Here is another proof for the greedy algorithm:
Let's forget w, and declare that each bottle contains m/n cups.
If n<m, then each bottle must be poured in two cups.
Consider the following graph:
Nodes are cups, and two cups are connected if they are filled using a common bottle.
The graph has m nodes, n edges. Consider a connected component, c its number of nodes. c cups need c*n/m bottles to be filled. On one hand, c*n/m<c, and on the other hand, there are at least c-1 edges. In the end, each connected component must be a simple path. Pouring in the order of each simple path is exactly the greedy algorithm.
Author said:
If N is odd, the correct formula is
which means ans(N) = f(N) / 2 + f((N + 1) / 2) when N is odd.
but actually, ans(N) = (f(N) + f((N + 1) / 2) / 2
DIV-1 (A)
in the first sample you can select the folders with 2 frames
you need to select folders (3,4)
then you can select folders from 5 to 9....
i saw the tutorial for this problem and i saw:
"and another tricky case: if the column where first folder is located is just at right from the column where the last column is located (21 5 3 12)"
i think this case could explain my solution for the first sample...