Закончился очередной этап кубка.
Как решать I нормально? Сначала думали, что это просто сесть и написать, потом оказалось, что следить за текущими картами в колоде довольно нетривиально.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
38:52:42
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
38:52:42
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 02:42:19 (k1).
Десктопная версия, переключиться на мобильную.
При поддержке
Закончился этап. С удивлением обнаружил команду моих студентов с 4-мя задачами и временем последней успешной попытки на 1:27. Говорят очень математические задачки, много конструктивов — не придумывалось. Как вы думаете, правда?
Да, так и было. Задачи были интересные, и очень хочется узнать решения задач. Хорошо было бы если опубликует разбор с авторскими решениями.
Ну из задач, которые они не сдали, задача B (http://opencup.ru/files/ocg/gp8/problems1.pdf) — совершенно классическая задача на динамику по профилю, никакой математики. Так что хотя бы пять нужно было сдавать :)
Да только она была предпоследней по сложности :-) Писать её было долго 40-50-60 минут (2 разные динамики нужны были) и после этого это могло получить тл, поэтому мы не стали её писать.
Да, задача не супер простая, но как верно отмечает ниже PavelKunyavskiy, динамика там одна. Вторая получается транспонированием обеих матриц и заменой p на 100-p.
(Чтобы это доказать, представим себе новые вершины в центрах квадратов старой сетки, и будем разрезать сверху вниз)
Да я видел. Мы к этому не смогли прийти на контесте, не очень это очевидно.
Нужно было хотя бы шесть сдавать! Я вот после того как понял, что слишком глупый, чтобы решать математику, сел и сдал две классические техники (B и I) :)
Рассакажите, как F решать, пожалуйста
Необходимо и достаточно, чтобы p и q были взаимно просты и имели разную чётность.
По одной координате мы должны получить ap + bq = 0, это a = kq, b = - kp. По другой up + vq = 1, это какое-то линейное представление НОД, одно из которых можно найти расширенным алгоритмом Евклида.
В этот момент стоит решить на бумажке какой-нибудь нетривиальный пример типа p = 2, q = 7 и понять, как связаны с ответом эти a, b, u и v.
Спойлеры: код и длинный текст решения с доказательством минимальности.
Мы воспользовались немного альтернативной идеей написать решение, которое пробует buben1 решений одного уравнения и buben2 решений другого, и проверить, что при изменении бубнов ответы не меняются.
Да, так даже проще: несложно показать, что хватит перебора O(1) пар решений, близких к минимальным по абсолютной величине.
Например, у команды Shanghai JTU Dreadnought, которая вскрыла эту задачу через 20 минут после начала, именно такое решение, и buben1 = buben2 = 11 (от -5 до +5).
Как решать C?
TL;DR Курить сюда
Если в кратце — задача про равенство элементов свободной группы. Надо понять что это за группа, и проверить как равенство в ней. В группе есть элементы степени 2, 3 и 5, значит она размера кратного 60. Можно доказать, что если взять любую группу и элементы, в которой выполнены эти соотношения максимального размера, то достаточно проверять равенство в ней (в одну сторону понятно, в другую это не совсем тривиальный алгебраический факт). На самом деле это группа изоморфна четным перестановкам длины 5.
Еще для желающих можно об этом думать как о вращениях икосаэдра (Кажется Petr сдал именно так). Мне попытка понять как перенумеровываются вершины при повороте вокруг оси, проходящей через середины противополныжных ребер несколько расширило сознание.
Еще есть магия от Egor и компании, которые долго подбирали и подобрали какой-то набор замен, каконинзирующий строку, если я правильно поняд. А так подразумевалось как гроб.
Do you know how to prove that there are only 60 equivalence classes and not more?
Well, at least i belive to wiki. We did something like that on algebra course. Some group counting with mormilizers and stabilizers. I don't remember exectly which. Also, we can recuce everything with length at least 14, so probably brute force can do it.
«Магия от Egor и компании» — это я, на самом деле.
Будем применять следующие преобразования перебором глубины не более 4, и если длина уменьшилась или осталась такой же, но строчка лексикографически уменьшилась, то сохраняем изменения.
00 →
111 →
0101010101 →
011011 → 101010
110110 → 010101
10101 → 0110110
010110101101 → 101101011010 и обратно
Не спрашивайте, как это придумать и почему работает :)
Мне не хватило преобразований 10101 -> 0110110 и 010110101101 -> 101101011010 :(
Я полагаю, что ты сидел и выписал тождества на ноликах-единичках, которые выводятся из соотношений, данных в условии. Откуда берутся первые пять штук я понимаю, я к ним тоже пришел. Но вот чем мотивируются последние два мне непонятно, можешь все-таки для меня пояснить? (мне понятна эквивалентность, мне непонятно, почему именно они)
Я целью всего этого действа видел скорее избавление от двух подряд идущих единичек, поэтому интересно узнать хотя бы эмпирические соображения, как до этого дойти.
Смотри, долгое время, пока я действительно делал всё на бумажке я сильно верил, что достаточно делать вообще только:
10101 → 0110110 и обратно
перебором на сколько-то вглубь, каждый раз убирая жадно все 00, 111 и 0101010101 и выбирая наилучшее из увиденного.
Кучу моих примеров это проходило.
Потом пришлось 0110110→10101 чуть-чуть переформулировать на 011011 → 101010 и 110110 → 010101, что почти не меняет дела.
Мне дали комп, я закодил и получил WA. Написал стресс-тест, увидел две вот те длинные строки, проверил на бумажке, что они не подходят под предыдущее предположение, поверил, что это последний особый случай — сработало :)
Паш, как задача может предполагаться как гроб, когда в википедии по статье "задание группы" (!) черным по белому указана группа, описанная в условии? Сложность в задании вращений икосаэдра? Без обид, но мне бы совесть не позволила дать на тур настолько легко гуглящийся математический факт.
Я более чем уверен, что если бы мы разрешали себе пользоваться гуглом во время соревнования (да, я знаю, что правила открытого кубка это разрешают, но мы ставим себе целью подготовку к финалу, и поэтому такими возможностями не пользуемся принципиально), то мы бы эту задачу сдали практически сразу, так как во время тура мы прекрасно понимали, что задача на самом деле об исследовании структуры некоторой группы.
При всем при том, от задачи у меня скорее положительные впечатления, все-таки узнал для себя что-то новое и клевое.
UPD: только увидел, что в этой статье еще и эквивалентность A5 указана, значит, никакие вращения задавать не требуется. Решение вообще в десяток строк выходит :(
Все-так онсайт имеет чуть больший приоритет, а там инета нет. К OpenCup я всегда больше отношусь как к образовательному и тренировочному контесту, по этому гуглить или не гуглить — выбор команды, и прокачивать скил гугления тоже не так плохо. Ну и было б из чего выбирать :(
Тут уже вопрос к snarknews, насколько он понимает, что некоторые проблемсеты готовятся из расчета на определенную аудиторию/правила, и что видение авторов (например, тебя), каким должен быть проблемсет, да и отношение к открытому кубку как к явлению может отличаться от его видения. Не уверен, например, что он согласится с твоим тезисом про тренировочность.
Насколько я помню, когда на последнем гран-при Екатеринбурга попалась задача на алгоритм Шраера-Симса (какое совпадение, тоже алгебра :) ), snarknews был крайне раздосадован этим фактом.
Ну "какое совпадение тоже алгебра" это логично, потому что в алгебре есть дофига алгортмических тем не раскрытых в олмпиадах (в прочем, может и к лучшему).
А про алгоритм Шраера-Симса... Между прочем был на одном вполне официальном соревновании (спойлер в предыдущих правках, не смотреть финалистам, отдельный привет Petr)
А как ты догадался бы, что надо гуглить по словам "задание группы"? По многим другим словам не находится. Например, есть ли хоть один поиск по-английски, который даёт нужный результат?
У нас на эту задачу осталось полтора часа. Мы пытались и решать, и гуглить. Гуглил сначала я по-английски, довольно долго, и ничего вразумительного не нашёл. Потом мы долго пытались решить сами, написали дфс, который нашёл классы эквивалентности для строк длины до 11 используя промежуточные длины до 23 (их кажется было 59 :)), но закономерностей тоже не нашли. Потом минут за 20 до конца meshanya сел погуглить по-русски, и довольно быстро нашёл эту статью в Вики. Потом нужно было за 10 минут вбить вращения икосаэдра, что, как верно подметил PavelKunyavskiy, несколько расширяет сознание, да.
С гуглением в целом есть проблема, что никогда не ясно, нужно ли гуглить дальше, или шансов нет. Поэтому сам факт, что информация есть в Вики, ещё не делает задачу простой.
Ну, я просто когда-то читал эту статью в википедии. Я бы начал с нее, а дальше, если бы не получилось, уже гуглил.
У меня получилось понять это вращение так: если представить себе икосаэдр как два повернутых на полугла относительно друг друга пятиугольника, плюс вершина сверху и вершина снизу, то мы при этом повороте просто меняем местами вершины сверху и снизу, и пятиугольники между собой. Единственная тонкость — как соответствуют друг другу вершины пятиугольников, но это тоже можно понять, нарисовав картинку.
Я нашел представление этой группы в перестановках 5, 6 и 10 элементов (т.е. подобрал такие перестановки x и y, что выполняются указанные в задаче равенства). Даже если бы группа была бесконечной, вероятность случайного совпадения перестановок у неравных строк только 4096^2/5!/6!/10! — малая величина, даже с учетом сотни тестов. Реально достаточно было представления в группе перестановок 5 элементов, но мы этого не знали.
А можешь пояснить аргумент с вероятностью подробнее?
Если бы скажем в этой бесконечной группе был элемент порядка, делящегося на 11, то вроде как эти перестановки не помогли бы его отличить от тождественного, так как у перестановок размера до 10 не бывает такого делителя порядка?
Я об этом не подумал. Но обычно в бесконечных группах порядок либо маленький, либо бесконечный. Бесконечный порядок, конечно, порождает другую проблему — можно взять слово в степени НОК(2,...,10) и мы его не отличим от тождественного. Но жюри могло и не додуматься до такого плохого теста, а на случайных тестах все хорошо.
А как посмотреть условия див.1?
Your text to link here...
Как решать задачу D?
У меня получилось сконструировать нечто подобное:
Т.е. на каждом из n/2 шагов делается ребро сначала в 2 (на следующих шагах 3, 4 и т.д.), а затем змейкой поочередно соединяются вершинки: левая-правая-левая-правая... Доказать почему это будет верно не пытался, но AC
Ссылка на фрагмент кода
Можно выделить центр, скажем вершину номер 1. А все остальные нарисовать на окружности. Тогда все ваши циклы получаются поворотом картинки. И понятно почему они не совпадают и покрывают все ребра.
Кажется это даже авторское решение. В целом, придумать явную конструкцию, так или иначе.
Как решать I?
При каждом перемешивании колоды надо помнить какие карты попали в это перемешивание. Теперь если про каждую карту, взятую втёмную, помнить из какой колоды она была взята, то можно ограничивать множество значений для этой карты, учитывая какие карты из этой колоды уже видны спрашивающему игроку, то есть какие карты уже в сбросе и какие карты есть в руке у этого игрока.
Остальное уже дело техники.
Да, всё так.
Мне кажется, немного проще не считать, какие карты из каждого решаффла уже видны спрашивающему, а считать, какие не видны.
У нас хранилось следующее: для каждой карты на руках каждого из игроков мы помнили, какого она цвета, взята она в открытую или в закрытую, и если в закрытую, то из какого она решаффла. Плюс мы помнили цвета 5 открытых карт, и количества каждого цвета в колоде и в сбросе.
Чтобы ответить на вопросы, нам нужно уметь понимать, какое максимальное число локомотивов может быть у заданного игрока, и какое максимальное число карт (цвет X или локомотив) может быть у заданного игрока.
Карты, взятые в открытую, учесть просто. Для карт, взятых в закрытую, нужно для каждого решаффла по отдельности взять минимум из количества закрытых карт этого решаффла на руках у заданного игрока, и общего количества карт нужного типа среди карт этого решаффла, неизвестных спрашивающему игроку. Последнее множество, в свою очередь, состоит из карт этого решаффла, взятых в закрытую всеми остальными игроками, плюс текущей колоды, если этот решаффл — последний.
Ну и нужно не забыть учесть, что если игрок спрашивает про себя, то он знает все свои закрытые карты.
F (рассказали выше, спасибо).
А у жюри было по H за куб решение, просто упростили?
У меня за куб, но было ощущение, что если сделать сильно больше, то могут начаться проблемы с точностью дабла. Тесты генерил в BigRational. Мой косяк, что не подумал про численное интегрирование, и оно оказалось на границе прохода.
На миптовых сборах месяц назад была задача "Bus Stop" с контеста AimFund, в которой предлагалось посчитать математическое ожидание максимума равномерно распределенных случайных величин ξ1, ξ2, ..., ξn, где ξi ~ U[0, ti]. Ограничения были n ≤ 105, и никаких проблем с точностью дабла (там во всяком случае) не было, а там еще, между прочим, было преобразование Фурье.
Я для своего решения умею объяснять, почему у него разумная абсолютная погрешность. Правило, к которому я пришел ещё на той задаче, заключается в том, что все интегралы должны быть в пределах от 0 до 1: тогда если мы посчитали коэффициенты многочленов без большой ошибки (в частности, если коэффициенты многочленов не растут экспоненциально), то интегрирование не добавит никакой ошибки (так как фактически интеграл будет линейной комбинацией коэффициентов многочлена с коэффициентами
)
Сегодня я вообще сдал решение за n5.
Вообще в Bus Stop были конечно проблемы с точностью в большей части решений. Чтобы их избежать надо было перейти к перемножению многочленов с положительными коэффициентами
Все-таки, на нашем контесте, проблемы с точностью у многих решений были.
Ещё в H есть такой забавный момент, что из-за маленьких ограничений координат задачу можно сделать дискретной. Мы считали вероятность, что "второй максимум окажется на отрезке [x,x+1), и всего на этом отрезке будет k точек, и верно ли, что первый максимум на том же отрезке". Это дискретная задача. А дальше мы просто говорим, что матожидание первой из k точек это k/(k+1), а матожидание второй из k точек это (k-1)/(k+1).
Ну кстати маленькие ограничения координат не по существу, можно то же самое сделать и со сжатыми координатами.
Как решать нормально задачи
CE и H? В задачеCE мы еле упихали тернарный поиск, а в H пытались численно брать интегралы, но получали WA2.А как решать С тернарником?
Извините, опечатался. Задачу E, конечно же, про точки на прямой. Решение задачи C тоже интересно, но его уже написали вверху. :)
Problem H: 1. First I divided the whole range into segments (sorted start/end ends of the segments) 2. Done numerical integration for all these ranges (adaptive simpson) 3. Now the question is how to compute the probability of x being the second maximum. 4. First run a loop to select the segment where this "second maximum" x belongs to (say i) 5. Run another nested loop to select the segment where the "first maximum" lies (say j) 6. Now run another loop through all the segments, if it is j, find the probablity for selecting number greater than x, if it is i, do nothing (it contributes dx of the integration), for other segments multiply the probability for selecting number less than x. 7. Sum these up to get the probability of x being on the i'th segment. (You need to divide by the length of i'th segment) 8. Multiply the sum with x to get the "expectation".
How to solve B?
R <= 9 or C <= 10. Both cases can be solved by bell number DP.
I have been always afraid of implementing this bell number dp. I was wondering if your code is simple enough. Will it be possible to share? Thanks.
Yes, the code is indeed quite long (like 4KB).
Oh, I made a terrible mistake, R × C ≤ 109 instead of R, C ≤ 109. Thanks QwQ.
Btw, it is same dp, if do second one on dual graph.
Может кто-нибудь объяснить, почему в G (Div2) работает просто перебор случайных чисел (и даже простой цикл до 15000 с проверками доступности единицы на каждом шагу)? Ведь вероятность найти нужную вершину, из которой можно пройти в единицу, очень мала (всё же их аж 2^32 штук). А если переходы есть только между 3% вершин, то вообще невозможно. P.S. И как усиливает безопасность запрет использования модуля random в питоне? В кларе ответили, что запрет из-за того, что питон лезет в /dev/random, но как использование этого устройства может обойти проверки безопасности?
В ejudge довольно строгие политики безопасности и запускаемый модуль получает минимум прав. В частности, при запуске Питона в secure mode обращение к /dev/random считается нарушением политик безопасности (прямое обращение к объекту извне контейнера, насколько я понимаю).
Причём, что интересно, в ранних версиях Питона random был реализован как-то иначе и обращения к /dev/random не было.
А ставить insecure на контест из-за этого не хочется.
Ставить insecure необязательно.
Что это значит? Что между остальными 97% вершин вообще попарно нет переходов? Это никак не следует из условия.
В условии написано другое: из любой вершины i в любую вершину j есть ребро с вероятностью p.
Например, из вершины 0 в вершину 1 есть ребро с вероятностью p.
И из вершины, например, 123456789 в вершину, например, 987654321 — тоже есть ребро с вероятностью p.
У нас есть граф из 232 вершин, между каждой парой вершин с вероятностью p есть ребро.
Пусть f(x) — вероятность того, что за x ходов мы успеем попасть из некоторой вершины, не равной 1, в вершину 1 (стартовое значение f(0) = 0).
Тогда мы пробуем из текущей вершины пройти в вершину 1, а если не получается, пытаемся идти в любую другую вершину, пока не получится. Можно записать формулу:
f(x) = p + (1 - p) * pf(x - 1) + (1 - p)2 * pf(x - 2) + ... + (1 - p)x - 1 * pf(1)
Вероятность того, что мы не справимся за 30000 ходов, равна 1 - f(30000) = 1.8 * 10 - 12.
А можно мне списать сабмит в C?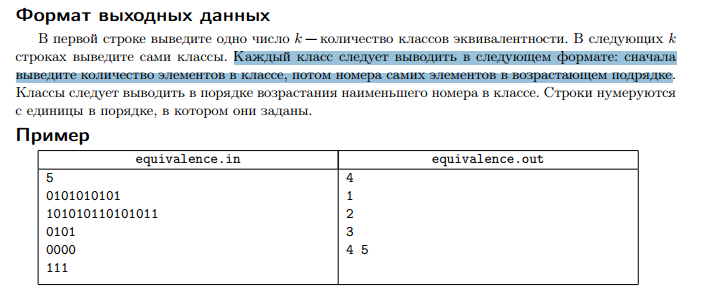
И какая проблема с этим?
В примере к задаче формат вывода другой -- не нужно выводить количество элементов в классе. Описанный в задаче формат тестер не принял.
Все решения с такой ошибкой пересужены с учётом изменения формата. В частности, 207-я попытка OK.
Как решать A?
Воспользоваться несколько раз формулой
Где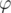
-- функция Эйлера.
Не совсем. Эта формула верна только для взаимно простых a, M. Там надо аккуратно учесть это (нужен не только остаток по модулю функции Эйлера, но и то является ли степень больше либо равна функции Эйлера).
Действительно. Совсем забыл про условие взаимной простоты.
Тем не менее, по задаче заходило ровно такое решение как я написал.
У вас (если khabarovsk01 это вы) не совсем так написано, всё время берётся по модулю 4 и 10 в цикле, и ещё начальное значение не берётся по модулю. То есть в какой-то момент берётся по модулю 10 то, что нужно далее по модулю 4, что в общем случае неправильно делать.
Тем не менее, числа в башне таковы, что можно считать не очень аккуратно. Если всё считать по модулю какого-нибудь большого числа, делящегося на LCM(10, φ(10), φ(φ(10)), ...) = 20 — например, по модулю 100 — то предпериод учитывать отдельно не придётся, так как на всех тестах у больших степеней больших чисел не получатся по такому модулю слишком маленькие остатки.
А еще можно использовать Wolfram Alpha и забить в код решения для всех a, b. С помощью Wolfram не удалось получить только ответы для a<9, b == 10, но там вид последовательности очень намекает, что он такой-же, как и при b == 9.
Собственно, это можно и руками сделать. Для каждого a можно быстро понять, что будет при всех b. Табличка-спойлер в правке.