The closest pair of points problem is a well-known problem in computational geometry (it is also in SPOJ) and several efficient algorithm to solve it exists (divide and conquer, line sweep, randomization, etc.) However, I thought it's a bit tedious to implement them, and decided to solve it naïvely.
The naïve algorithm is as follows: first, sort the points along the x axis, then, for each pair of points whose difference in the x coordinate is less than the optimal difference so far, compute the distance between the points. This somewhat heuristic algorithm fails when all of the x coordinates of the points are the same, so the running time is O(n2).
What I did to get an AC at SPOJ is pick up a random angle θ and rotate the points around the origin by θ at the beginning of the algorithm. This (I hope) makes the heuristic work and I got an AC.
The problem is the complexity of this randomized algorithm. Some say its average running time is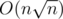 
. How do you prove this?
May be its better than O(n*sqrt(n)).
Your rotation part is not explained very clear. Did you rotate only once? In that case wouldn't the complexity be the same, as it would still fail test case where I first create lots of the points having same x coordinates (e.g. 100 groups of points far enough to each other) and then rotate each of them by pi/100, 2*pi/100, 3*pi/100... angle?
And your statement "average running time" is not very clear to me. Is it average on random set of points? Every possible set of points if run the problem multiple time? Or does it mean it is hard to create a fail test case?
I believe SPOJ's new problems' test cases are not too good, since everyone can become problem setter and add almost whatever problem they want.
I think the question is — we have set of points, rotate them by random angle (evenly distributed). Than we count average number of comparisions. Qustion is — what is the biggest value of this average?
I think what Egor has said is the same as what I meant. As for your test case, the main idea is that the probability of θ coinciding with any of kπ / 100 is negligible, so the "average" running time is less than O(n2).
I didn't need phi to coincide with any of the k*pi/100 angles. Please read my below comment for clarification.
Btw, just a bit curious, was the unclear of my idea the reason for the minuses?
After first point is checked against all others, the minimal distance will be less than distance between groups. So, why do you need "100 groups of points far enough to each other"?. It is not matter how far groups to each other.
Because I meant the minimum distance can not be between 2 points of different groups, which is the same as your statement "After first point is checked against all others, the minimal distance will be less than distance between groups". If I didn't state that, it may be not clear if it is the case.
I don't understand you. WHY groups are farther than MinDist. FOR WHAT we need groups?
If we have only 1 group, by your proof below, it is on average O(Nsqrt(N)). If we have K groups, it increases the range of your R, to something like K*R.
Oh, now i understand your idea. Please read my "proof" below. Let M = N / K, then R is about
K * acos(1 / M)so the avereage complexity is (N/K)^2 * K * (1 / M) = (N/K)^2 * K * (K / N) = NHi, I've been reading your comment the whole time :) and made my reply 2 minutes before yours :)
Извиняюсь, забыл переключиться на английский
If you first build Delaunay triangulation on set of points, closest two points will belong to an edge of one of triangles. Delaunay triangulation closely related to Voronoi diagram, that can be build by Fortune's algorithm with complexity O(n*log(n)). So overall complexity of "closest pair problem" is not larger than O(n*log(n)), but this approach with triangulation seems to be overcomplicated, possibly exists another much simpler way with the same complexity.
Well, he mentioned at least one such algorithm — Divide and conquer. The problem is it is still quite complex to implement
I don't know how to prove any estimate, sorry.
Some months ago I tried to construct testes against such algorithm, and failed to construct them. Of course it's not a proof, but...
I think that there are no testes against this idea, we can build only testes against some concrete, "not random enough", implementations. Just like as quicksort...
To R_R_ : suppose you divide all N points into K groups with approximately N/K points in each. When K is small, there is too large probability that no of these K groups becomes vertical. When K is large, we have not N^2 but only (N/K)^2. So the algorithm IS theta(n^2)-time in worst case, but the worst case has too small probability.
To ikk : How do you rotate points? My idea was to choose random numbers 0<A<100, 0<B<100, and transform each point as x_new = A * x_old + B * y_old y_new = B * x_old — A * y_old After this, we still can use integer arithmetics, and only after finding final result we divide it with (A*A+B*B) and apply sqrt.
Yes, I know that the points will not be vertical, but I tried to create the set such that the difference in x-coordinate when rotated is smaller than the minimal distance (with angle like 1 degree, the points should be almost vertical, so the difference between x-coordinate should be small, the only problem is the distance from each point to another may still be smaller than that). Thus whatever angle rotated, it is still O((N/K)^2) = O(N^2).
Some more explanation:
Set of points rotated by i*pi/100 is used to kill angle phi in range (i-0.5)*pi/100 to (i+0.5)*pi/100. With phi in this range, after rotation, this set of points will be very closed to vertical. Now we need to make sure that the algorithm can not be improved by using minimal distance so far. We do this by make sure of 2 things:
Difference set of points are far away from each other.
In a set of points, the points are far from each other. But this would increase the difference in x-axis by something like O(N*(min dist)*(some function with K)). So it is not too easy to create this set.
The test case I described is only my assumption, I have not tried to figure out the details (like how far away the points should be from each other, how big should K be, etc.), so maybe one cannot create such test case.
I don't think you have such test case with
O(n^2)operations in avereage with random angle. I have a "proof", it is not strict, it is not a proof for mathematicians, but these reflections have convinced me. I think avereage time isO(n*sqrt(n))At first step, lets consider simple test case, where all points are on the same line with distance 1.0 between each consecutive two points. We can to choose any angle from
[0, to 2 * Pi)and in most cases there will be linear time, but this part is not interesting for us. In the remaining part of angles there will be O(n^2) time. Range R of these angles is aboutacos(1 / n). ifn -> inf,acos(1/n) ~ 1/n. So, for this simple test case we haveR * n^2 + (1 - R) * n ~ 1/n * n^2 + (1 - 1/n) * n ~ noperations in average.Now lets consider more general case. We have some set of points S, and don't know how points are situated, but it has bounding rectangle with sides
A and B, A <= B, minimum distance between any pair of pints is 1.0. There is many lower and upper estimates for number of operations with different angle alpha F(A, B, alpha). It is hard for me to explain many of them in English, but i hope you can make it by yourself. The main thing iswhen A is stricly lower O(sqrt(N)) i.e. A / B != const, R tends to zero (vanish)For the simple case, your argument is not fully correct.
In range R, the x-distance between the first point and last point after rotation is 1, so for each point we need O(N) operations. (which I agree with you)
In range 2R, the x-distance between the first point and last point became 2, which means for the first point we need O(N/2) operations. For other points, we need a bit more. But let's just assume that the total complexity is O(N^2/2).
So, maybe the correct calculation should be done by using some integrals (my math doesn't allow me to do this, so I'm not sure). But for this simple case it may remain O(Nsqrt(N)) or something small.
Now, for my bigger test case (multiple groups), the complexity doesn't seem trivial without knowing the correct proof for the simple case :)
Simple test case is obviously O(n). We say about O symbolic, so constant factors can be omitted — that's why i say R is just acos(1/n) you can assume R is 100 * acos(1 / n).
Please read my comment with care :)
Whatever big R be, if complexity in range R is O(N^2), I can prove the complexity of range 2R is O(N^2/2), and it affect the total complexity.
So this is how I want to calculate it, which I believe is more correct:
And sorry if this is wrong, my math is very bad, I used to sleep a lot in math lectures :(. But I don't think your formula is correct.
And also, increasing range R like you did affect the proof of my test case.
Yes, simple test case seems to be NlogN in average, I am wrong, but i still don't think your test case O(N^2)
Yes, after reading your first comment, I also doubt my test case is O(N^2). I'm just wanting a correct proof :)
I decided floating-point numbers are OK and stuck with `pure' rotation (i.e., its determinant is 1).
S = Sin(alpha), C = Cos(Alpha)nx = C * x - S * yny = S * x + C * yor
S = rand(), C = rand(), D = sqrt(S * S + C * C), S /= D, C /= Dnx = C * x - S * yny = S * x + C * yИзвиняюсь, забыл переключиться на английский
It is easy to proof lower bound O(n*sqrt(n)): for set of points = {(x, y): x,y — integers, 0 <= x <= sqrt(n), 0 <= y <= sqrt(n) } we need to make O(n * sqrt(n)) operations with any angle.