161A - Оденьте их скорее!
Будем рассматривать бойцов в порядке сортировки, то есть так как они заданы во входных данных. Утверждается, что для текущего бойца всегда выгодно из всех неиспользованных подходящих бронежилетов выбирать тот, у которого bj минимально.
В таком случае задача решается используя метод <<двух указателей>>. Первый указатель двигается по бойцам. Вторым указателем подбирается минимальный по размеру бронежилет из неиспользованных такой, что bj - x ≥ ai.
Асимптотическая сложность решения O(n + m).
Автор идеи: Burunduk1
161B - Скидки
Задача решается жадным алгоритмом. Пусть у нас есть x табуреток. Можно доказать, что всегда выгодно min(k - 1, x) максимальных табуреток разложить в min(k - 1, x) корзинок по одной.
Все оставшиеся табуретки и карандаши нужно положить в оставшиеся пустые корзинки. Заметим, что либо у нас не останется табуреток, либо останется ровно одна пустая корзинка.
Авторы идеи: Burunduk2 и Burunduk1
161C - Абракадабра
Предположим, что максимальный по значению символ в строке входит в ответ. Тогда ответ равен min(r1, r2) - max(l1, l2). Предположим, что это не так. Тогда нужно разрезать каждую из строк по этому символу (в одной из частей может получиться пустая строка) и запустить алгоритм рекурсивно от каждой из полученных пар строк. Можно доказать, что это решение имеет сложность O(K), где K — значение максимального символа.
Другое решение:
Задача решается перебором старшего (то есть, наиболее редкого) символа, который будет находиться в наибольшей общей строке. То есть, если x — старший символ, который встречайтся в обоих строках, и (это важно) в строках не встречаются более редкие символы, то ответ считает по несложной формуле. Второе условие (в строках не встречаются символы, более редкие, чем рассматриваемый) может, вообще говоря, не выполняться. Но его легко достичь, заменив строки на списки строк: если сейчас рассматривается символ x, то вместо каждой из строк у нас будет по несколько строк: изначальные строки, разбитые символами, которые старше x. Причём в каждом списке имеет смысл хранить не более двух строк: если более редкие символы разбивают на три и более подстроки, то среди этих подстрок встретятся «полные» строки. Например, если строку badabaca разбить по символам не младше c, получится список ba, aba, a. Очевидно, что из этих трёх строк достаточно оставить одну aba. Осталось научиться дробить строки и считать ответ для фиксированного старшего символа. Для этого рассмотрим, как зависит символ от позиции в строке.
Здесь удобно нумеровать символы строки с единицы, тогда:
- на нечётных позициях стоят символы «a»
- на чётных позициях стоят символы «b» и старше
- на позициях, кратных четырём, стоят «c» и старше
- на позициях, кратных восьми, стоят «d» и старше
- и так далее, символ соответствует степени двойки, входящей в номер позиции
Используя эту закономерность, можно проверять, лежит ли в строке символ x или старше, и находить его позицию. Для этого достаточно найти минимальную степень двойки, не меньшую левой границы строки. Если она не выходит за правую границу, это и будет ответ.
В итоге решение может быть следующим:
- Перебираем символы, начиная со старшего. На каждом шаге храним два списка: подробленную первую подстроку и подробленную вторую. Изначально эти списки содержат по одному элементу, собственно, исходные строки.
- На каждом шаге перебираем пары строк из имеющихся списков и проверяем,лежит ли текущий символ в каждой из выбранных подстрок. Если лежит — обновляем ответ.
- Перед тем, как перейти к следующему (то есть, более младшему) символу, переразбиваем списки строк. Если в каком-то списке окажется хотя бы три строки, то из них можно оставить вторую (она гарантированно будет полной строкой соответствующего уровня).
Автор идеи: avm
161D - Расстояние в дереве
Эту задачу можно было решать методом динамического программирования. Подвесим дерево за какую-нибудь вершину. Для каждой вершины v дерева, посчитаем значания d[v][lev] (0 ≤ lev ≤ k) — количество вершин в поддереве, расстояние до которых равно lev. Заметим, что d[v][0] = 0.
Далее по этим значениям посчитаем ответ. Ответ равен, сумме по всем вершинам v двух величин:
- Количество путей длины k, которые начинаются где-то в поддереве вершины и заканчиваются в самой вершине. Это количество очевидно равно d[v][k].
- Количество путей длины k, которые начинаются где-то в поддереве вершины и заканчиваются в где-то в поддереве вершины. Это количество равно сумме по всем сыновьям u вершины v величины
.
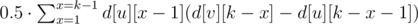Считаем сумму по всем вершинам. Получаем решение за O(n·k).
Автор идеи: Burunduk1
161E - Медвежатник Поликарп
Необходимо посчитать количество симметричных матриц с заданной первой строкой, каждая строка которой представляет собой простое число.
Так как матрица симметричная, то она полностью определяется своими элементами не ниже главной диагонали. Переберём все возможные значения цифр, которые находятся в клетках выше главной диагонали (не более 106 вариантов). Заметим, что теперь значения оставшихся неопределёнными цифр, которые стоят на главной диагонали, независимы между собой, так как каждое из них влияет ровно на одну строку матрицы. Поэтому достаточно независимо посчитать количество возможных вариантов для каждой из цифр на диагонали и перемножить полученные значения, чтобы получить количество способов дополнить матрицу до требуемой.
Более того это количество можно предподсчитать заранее для каждой неизвестной позиции и для каждого набора уже известных цифр. Такое решение уже укладывается в ограничение по времени.
Можно было пойти и дальше, отсекаясь при переборе значений цифр выше главной диагонали, если после добавления очередной цифры её строку или столбец больше нельзя было дополнить до простого числа (возможность это сделать так же можно предподсчитать заранее). Данное решение позволяет найти ответы для всех возможных тестов за отведённое время, но это не требовалось.
Автор идеи: avm
Задачи раунда готовили (в алфавитном порядке): arseny30, at1, avm, Burunduk1, Burunduk2, burunduk3, Gerald, levlam, MikeMirzayanov, Nickolas, vysheng
Количество Burunduk -ов слишком велико на одного автора.
Стандартное количество бурундуков.
Three Burunduks walk into a bar. "Accepted", — said the bartender.
Жадный раунд
Извиняюсь за глупый вопрос по А.
Почему это не проходит, а вот это получает АС.
Вроде бы просто обернул цикл
while (t2 < m && b[t2].first < a[t1].first) t2++; if (t2 == m) break;в строчкуif (b[t2].first < a[t1].first) { t2++; continue; }?потому что в первом варианте, когда не выполнится условие b[t2].first < a[t1].first, может оказаться, что бронежилет слишком большой, т.е. b[t2].first > a[t1].first + y
Поясните, пожалуйста, почему в первом решении не получится 4^K, если мы начнем делиться в каждом слове на каждом шаге
Если мы какое-то слово поделили, то оно всегда будет либо суффиксом, либо префиксом строки. Если мы его поделим еще раз, то одна половина будет совпадать со всей строкой, а значит длина наибольшей общей подстроки будет равна длине второй строки. Получается, что каждое слово раздваивается не более раза.
Nice :) Problem D could also be solved much faster using Splay Tree... if you sort the solutions by execution time, you can see all the fastest ones used this. Oh and hey, they all used actually the exact same code:
1343350 by XusuoFestival rank 235
1342455 by suhang1994 rank 147
1343283 by whitesky rank 403
1343446 by mjmjmj rank 207
And so on... what a coincidence that they all have the same code.
1349546 is even faster asymptotically, it's just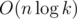
. That's because it uses hash tables instead of splay trees.
How is it using hash tables? The solution looks like it is just the N*K dp solution using an iterative dfs by a manual stack. Can you explain further how the solution works algorithmically? I don't use python much.
O(nk) solution won't pass in Python because of it's high overhead.
Here's the same algorithm in Java:
Sorry I really can't see at all why this solution would be O(n log k). Isn't
for (Entry<Integer, Integer> e: result2.entrySet())going to go through all k values in the map? And you are doing this for all children of all nodes. If that is so, it will be O(nk).Read the large comment very carefully.
It says that there are two types of merges: when both subtrees of size at least k and when one of the subtrees has size less than k.
The first type merges can only be done n / k times. So it gives O(n), for all merges, since one merge is done in O(k).
In the second type of merge, since you iterate over map of small subtree and add them one by one, every vertex will be iterated over O(log(k)) times, because every time it is being iterated over, the size of its subtree gets twice larger. Since it is in subtree of size at most k, this vertex is touched O(log(k)) times, while it takes part in second type of merges. So this gives O(n log(k)).
Thanks to all who replied. I think I get it, but it isn't got to do with the hashing at all right? In fact I can do this same optimization with the O(nk) DP by remembering the maximum length reached for the node so far, iterating over the smaller of the current array and that of the next child and propagating a pointer to the current maximum length array...
It is. You can add to Hash Table in O(1) time, so k additions give O(k).
Everything you do is iterating over Hash Table, adding and search for elements in it. Iterating is O(1) time per element, addition and searching is O(1).
The solution is O(n log(k)) operations with Hash Table, since all of them are done in O(1) time, you get overall solution complexity O(n log(k))
I didn't get your point at first.
It seems that you are right.
Look carefully at this:
I always iterate over the smaller of the two maps. Every time I go through a value, I move it to a map which becomes at least twice larger. That's why I go through each value at most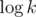
times.
There is also a solution using divide and conquer that runs in N log N for arbitrary K. My solution (1346501) implements this idea except I was lazy and did the N log^2 N version. Change the graph splitting step to be O(N) instead of N log N and my solution becomes N log N. The N*K is easiest to code for this bound though. =) I like this problem because of the variety of approaches that can be used.
Here is the N log N version: 1354146
N*log(N) with a simple idea (1353450, from "vvi graph");
It's actually very obvious that they are copies, because if you look at the start of int main, they all have this: ~~~~~ e[++l]=y,next[l]=lis[x],lis[x]=l;cost[l]=1; e[++l]=x;next[l]=lis[y],lis[y]=l;cost[l]=1; ~~~~~ Notice the commas and the semicolons. They both made the same formatting inconsistency.
А расскажите кто-нибудь, можно ли D вырешать как-нибудь пооптимальнее? А то на питоне 25 лимонов ну никаким боком не лезут, а на С ее писать слишком скучно.
Говорят, что можно.
И правда... Прикольно, спасибо! 1349546
Нашел в своей комнате забавное решение 1343627.
Суть. Найдем количество вершин, удаленных от каждой вершины дерева не более, чем на k-1 и на k-2. Покажем, как из этого вывести количество вершин, удаленных не более, чем на k от данной. Пройдем из данной вершины по ребру во всех соседей и сложим значения для путей длины не более k-1 в них. Но мы могли по тому же ребру вернуться в исходную вершину, каждый такой путь соответствует пути длины не более k-2 из исходной вершины. Вычтем их.
Таким образом, динамика строится без обходов графа двумя вложенными циклами с одной операцией внутри.
E можно решить за O(1) на запрос и разумный предподсчет (не сохранение всех ответов в код, а именно предподсчет).
Будем писать числа в матрицу сверху вниз построчно. Перед последним числом матрица будет выглядеть как-то так:
Здесь X и O — какие-то числа, . — свободное место. Поскольку от X ничего не зависит, посчитаем количество способов дополнить до корректной матрицы для всех возможных вариантов O, это легко сделать. Удобно параметризовать варианты числами от 0 до 9999.
Дальше, пускай до полной матрицы не хватает двух чисел:
От X опять ничего не зависит, вариантов для O — 10^6, параметризуем двумя числами от 0 до 999. Как удобно считать ответы: перебираем число на места O для последней строчки и простое число целиком (возможно, с ведущими нулями) для предпоследней. Если последнее число — a, а простое — p, получаем переход из состояния (p / 100, a) для двух свободных строчек к состоянию (10a + p % 10) для одной последней строчки.
Для трех и четырех строчек переходы такие же. После предподсчета любой запрос сводится к одной из предыдущих задач, например:
9001:
Примерное количество операций — количество простых чисел до 100000 * 10^4, т.к. это самое большое число вариантов для чисел в нижних строках.
На Е можно получить Accepted просто перебором с оптимайзом. Жалко, мои навыки еще немного не дотягивают до Burunduk1 поэтому я чуть-чуть слажал.
Не сомневаюсь. Но будь количество запросов большим, перебор бы не прокатывал.
Could you explain how to prove the O(k) bound for running time in C?
For convenience we define a substring as a interval on a segment [1,2^p-1], where p marks the depth of recursion.
The main point of the standard algorithm is to divide a request on [1,2^p-1] into at most 2 requests on [1,2^(p-1)-1].(2 is correct, because when there are 4 subrequests two of them can be regareded trivial. See next paragraph.)
It's obvious that if one of the interval in request is full or empty,this request can be solved in O(1) without recursion.We call these requests trivial.(Futhermore, when a interval is totally covered by the other,this request can be regarded trivial. So requests of two prefixes or suffixes are trivial, because the condition of covering is hold.)
Similar to a segment tree, we can prove that on each level of recursion, there will be at most 2 non-trivial interval of substring A,2 non-trivial interval of substring B,so the maximal non-trivial requests on each level is 4.
thus,the time complexity for the recursive algorithm is proved O(k).
I don't think it's that simple or perhaps I misunderstood something. You say that a single request on level p results in 4 requests on level p-1. This gives you exponential time complexity, not linear.
It's correct that single request on level P can result in 4 requests on level p-1, but this means all 4 requests on level p-1 are non-trivial. That is, No more non-trivial requests on level p-1. Linear time complexity still hold.
If you dont understand, think why a interval on a segment tree can be divided into two intervals on next level, but its time complexity is O(h),not O(2^h), where h is the height of segment tree.(at most two non-trivial intervals on each level.)
(Sorry for my poor expression...As a Chinese,I'm not a native speaker of English.)
I disagree that all 4 requests are trivial. I'll give an example with k=3. Lets say we have the following request L1=3, R1=6, L2=5, R2=12. We divide it into two requests on level k-1: L1=3, R1=6, L2=5, R2=7 and L1=3, R1=6, L2=1, R2=4. These two requests are not trivial. You would have to go at least one step further to prove that you are left with just trivial requests in some small, constant number of steps.
What's written before is "this means all 4 requests on level p-1 are non-trivial." I think your example makes no sense this time.
"Заметим, что d[v][0] = 0." Почему 0? Разве расстояние от v до v не 0? Значит одна такая вершина имеется. "Количество путей длины k, которые начинаются где-то в поддереве вершины и заканчиваются в где-то в поддереве вершины." Точнее, заканчиваются они где-то в другом поддереве вершины? А в формуле кол-ва путей сумма видимо ещё и по u -- сыновьям v?
Наверное, всё-таки
d[v][0] = 11355198
В разборе задачи А мы берем такие i, j, что b[j]-x >= a[i], т.е. a[i]+x <= b[j], хотя в условии дано a[i]-x <= b[i].
Здравствуйте я немного не понял про задачу Расстояние в дереве. Какую брать величину lev?
Нужно посчитать значение динамики d[v][lev] для ВСЕХ lev от 0 до k.
Если что — вот закомментированный короткий код.
I want to ask that can Problem D is solvable by applying DFS of k length on each and every vertices??? Please reply admin...
If you try that on the following graph:
you would perform O(n^2) operations when k >= 2.
Как в задаче 161D доказать, что ответ помещается в long? Другими словами, как оценить количество путей на графе из N вершин длиной K?
Из каждой вершины может быть не более N путей, значит всего в графе будет ну уж никак не больше N * (N — 1) / 2 путей, ну а 50000 * 50000 спокойно влазит в long.
Действительно, путей не может быть больше, чем пар вершин, то есть оценка сверху N * (N — 1) / 2. А оценка снизу — при всех вершинах, соединённых с первой, есть путь длиной 2 между любыми двумя вершинами, кроме первой, то есть оценка снизу для вполне возможного максимального ответа (N — 1) * (N — 2) / 2.
Получается, что при ограничениях задачи ответ помещается в 32-битное целое число со знаком. Другое дело, что если последняя операция деление на 2, то то, что делится на 2, в 32-битное со знаком уже не помещается, так что можно использовать 64-битные числа, а можно извращаться с нецелевым использованием знакового бита 32-битного числа.
А можно не извращаться, а просто использовать беззнаковый 32-х битный тип.
Самое очевидное решение, если язык беззнаковые типы поддерживает. Однако некоторые языки, например Java, беззнаковые типы не поддерживают.
I have written a tutorial about VK practice session but I can't attach it to the corresponding site. What can I do?
In problem D's tutorial(above), for each v, d[v][0]=0;
Now for first test case,
for vertex 2, first value is 1. for second value- 0.5(d[3][0]*(d[2][1]-d[3][0])) + 0.5(d[5][0]*(d[2][1]-d[5][0])) = 0(as d[3][0]=0 and d[5][0]=0), but shouldn't it be 1(for path 3->5). Please tell me where am i going wrong.
Thanks..
d[v][0]=1 ( Base Case ).
Because the vertex v is itself a part of its subtree.
Taking d[v][0]=0 gives wrong answer.
Can someone explain the recurrence relation for problem D?
How did they get d[u][x-1](d[v][k-x] — d[u][k-x-1])?
We are iterating over the subtree where one end of the path is (u). The path consists of two segments: - one inside of u's subtree (length is x, which we apart iterate over), there are d[u][x-1] of them - another one outside of u's subtree (but still within v's subtree), the length of this segments is k-x (counting from v); there are d[v][k-x]-d[u][k-x-1] of them
Give or take ±1 everywhere:) it's been 8 years after all.
Why did they subtract d[u][x-1] — d[u][k-x-1]?
Sorry, I'm new to dp so I don't know how to get the recurrence relation.
It's a bit different as compared to what you wrote.
The overall amount of vertices in v's subtree on depth (k-x) is d[v][k-x]. We should not count the vertices that are in u's subtree though, because in this case we are looking only at the paths that would go through v. So we have to subtract that amount, which is d[u][k-x-1]. The (-1) here is because u is exactly one level below v.
This might help : https://mirror.codeforces.com/blog/entry/76080?#comment-604916
I have tried to write a beginner friendly solution for D :)
Did someone solve D using LCA in O(1) per query? My attempt: 140424972
O(1) per query still makes it O(n^2) which obviously won't pass.
Задача D,d[v][0]=1
I had a pretty hard time understanding the solution for D. In my opinion, the easiest way to understand it is to look at the implementation of it at: https://www.geeksforgeeks.org/find-the-number-of-distinct-pairs-of-vertices-which-have-a-distance-of-exactly-k-in-a-tree/
The program goes from bottom to the top of the tree, and you calculate for each vertex the number of paths that are length k, and go through that vertex AND none of the paths go through the parent vertex (because you will calculate for parent vertex later on).
Note, that array d is used sth like this: d[vertex_i][distance_x] == number of children (aka number of vertices in the subtree of vertex_i) that are for distance_x away from that vertex_i (which is "root" in that subtree).