** UPD : Считается, что все формулы уже исправлены **
163A - Подстрока и подпоследовательность
Кратко о решении: динамика.
Одно из авторских решений: 1415300 (автор = levlam)
Задача решалась следующей динамикой. Пусть f[i, j] — количество равных пар вида "подстрока начинающаяся в позиции i" и "подпоследовательность подстроки t[j..|t|]".
Тогда:
f[i, j] = f[i, j + 1];
if (s[i] == t[j])
add(f[i, j], f[i + 1, j + 1] + 1)
Answer = 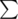 f[i,0]
f[i,0]
Кратко о решении: сортировка + бинпоиск по ответу.
Одно из авторских решений: 1415306 (автор: Burunduk1)
Нам нужно найти минимальное время T. Давайте сделаем бинарный поиск по ответу.
После этого можно расставлять леммингов жадно или снизу вверх, или сверху вниз. В этом разборе я воспользуюсь способом <снизу вверх>. Из тех леммингов, которые могут забраться на 1-й уступ, выберем лемминга с минимальной массой, а из таких — с минимальной скоростью. Почему так можно сделать? Пусть мы поставили на первый уступ лемминга с большой массой, значит, всех леммингов с меньшей массой мы использовать уже не можем, значит, можно было поставить на первый уступ любого лемминга с меньшей массой. А из леммингов с одинаковой массой всегда выгодно оставить тех, чья скорость больше, они могут залезть на более высокие уступы.
Чтобы быстро расставлять леммингов в таком порядке, отсортируем их заранее, сравнивая сперва по массе, затем по скорости. После этого мы рассматриваем всех леммингов в порядке возрастания массы ровно один раз и каждого или берем, или не берем. Второй раз рассматривать лемминга не имеет смысла, т.к. или мы его уже взяли на i-й уступ (он занят) или мы его на i-й уступ взять не смогли, тогда на i + 1-й и т.д. тоже не сможем.
Итого решение = сортировка + бинпоиск по ответу с линейным проходом внутри. Время работы = O(Nlog?)
Но написать бинпоиск и верную жадность в этой задаче было не достаточно для получения Accepted. Нужно было еще не попасться на проблемы с точностью. Давайте точно оценим число итераций бинпоиска.
0 ≤ T ≤ H * K (максимальное время не больше 109). Нужно понять, насколько могут отличаться два времени. В случае "N = K = 105, H = 104, V порядка 109" времена, за которые некоторые два лемминга поднимаются на какие-то уступы, могут отличаться на 10 - 18. Это следует из того, что времена = рациональные дроби 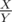 , где X и Y порядка 109.
, где X и Y порядка 109.
Т.е. нам нужно сделать число итераций = log21027 = 90. На практике моему решению 70 итераций не хватало, а вот 75 было уже достаточно. Рассуждения выше показывают, что 90 точно хватит.
Кратко о решении: события на окружности или бинпоиск.
Одно из авторских решений: 1415310 (автор: Burunduk1)
Одно из авторских решений: 1415316 (автор: arseny30)
Антон, откуда бы он ни начал, пробежит по конвейеру отрезок длины D = (v2 * l) / (v1 + v2). Рассмотрим одну конфету. Чтобы ее скушать, нужно попасть на конвейер в любой момент из отрезка [ ai — D .. ai ]. Рассмотрим все точки вида a[i] — D и a[i] , если какие-то из них отрицательны, прибавим 2 * l. Также не забудем добавить в массив точек числа 0 и 2 * l. Отсортируем эти точки. Рассмотрим теперь две соседние — x[i] и x[i+1]. В какой бы момент времени между этими двумя точками Антон ни начал, он съест одно и то же количество конфет.
С этого момента можно получить одно из двух решений:
1) Запуститься от каждой середины отрезка M = (x[i] + x[i+1]) / 2 и бинпоиском по отсортированному удвоенному массиву a найти количество конфет на отрезке [M..M + D].
2) Сказать, что у нас есть события на окружности вида (a[i]-D,+1) и (a[i],-1). Нужно пройти по кругу два раза, и на втором проходе говорить, что мы знаем, сколько раз покрыт текущая точка конфетами-отрезками.
Оба решения работают за время O(NlogN).
Кратко о решении: перебор с отсечением по ответу
Одно из авторских решений: 1415320 (автор: Burunduk1)
Решение состоит из трех главных идей:
V = ABC, A ≤ B ≤ C тогда A ≤ N1 / 3, B ≤ (N / A)1 / 2.
A и B — делители V, а поскольку нам уже дано разложение числа V на простые множители, можно перебирать только делители
Если зафиксировано A, то оптимальные вещественные B и C = (N / A)1 / 2 (обозначим эту величину за X). Т.е. площадь поверхности получится в любом случае ≥ 2(2AX + X2). Таким образом можно использовать отсечение по ответу.
Если применение в лоб этих идей давало TL, то можно было воспользоваться следующими оптимизациями:
Отсечение по ответу лучше работает, если перебирать A в порядке убывания
A и B — 32-битные целые.
Если мы для числа V уже считали ответ, то нужно запомнить ответ (таким образом мы чуть уменьшили max тест).
Если кому-то интересно теоретическое обоснование "Почему это все работает за нужное время?", приведу некоторую статистику:
Максимальное количество делителей у чисел от 1 до 1018 = 103860 (у числа 897612484786617600 = 2834527211 ...)
Если использовать только 2 первые оптимизации, количество чисел A, которое переберет наше решение = 10471 (на числе с max количеством делителей)
Если использовать только 2 первые оптимизации, количество пар A и B, которое переберет наше решение = 128264 (на числе с max количеством делителей).
163E - Электронное правительство
Кратко о решении: Ахо-Корасик + сумма на пути в дереве суффиксных ссылок
Одно из авторских решений: 1415345 (автор: arseny30)
Предполагается, что читатель знаком с алгоритмом Ахо-Корасик (прочитать о нем можно здесь http://e-maxx.ru/algo/aho_corasick).
Пусть у нас есть бор имен и суффиксные ссылки на этом боре. Также для каждой вершины v посчитано количество имен, кончающихся в этой вершине (end[v]).
Тогда добавить имя i: end[v[i]] += 1, где v[i] — вершина-конец i-го имени
Удалить имя i: end[v[i]] -= 1.
Чтобы ответить на запрос "политизированность текста", нужно увидеть, что суффиксные ссылки образуют дерево. Когда мы проходимся по тексту и параллельно ходим по бору с суффиксными ссылками, если мы находимся в вершине бора v, нужно прибавить к политизированности сумму end[v[i]] на пути по суффиксным ссылкам от v до корня дерева. Теперь нужно научиться быстро решать задачу <сумма весов вершин на пути до корня, веса меняются>.
Это можно сделать например так:
Говорим, что вес не в вершине, а на ребре, соединяющем вершину с ее отцом.
Храним Эйлеров обход дерева, в котором при спуске вниз записан плюс вес ребра, а при подъеме наверх минус вес ребра.
Сумма на пути до корня = сумма на отрезке в Эйлеровом обходе (концы отрезка — произвольные вхождения двух вершин в Эйлеров обход).
Быстрый и удобный способ считать сумму на отрезке — дерево Фенвика.
Мы получили решение работающее за время O(|SumLen| * log). Памяти используется |SumLen| * 26 (бор мы храним не сжатым).











Есть такой спецэффект, что решения авторов контеста нельзя посмотреть. Вот совсем. И в списке посылок их тоже нет.
Скоро дам доступ на эти решения.
Дал доступ к просмотру.
Thanks for the editorial. Please provide an English edition. Meanwhile I noticed that the author's submissions aren't accessible at this moment.
I'll give access to the solutions soon.
Fixed
Я в D придумал решение за (количество делителей * количество различных простых) на тест. Правда набажил и еще не заработало) Как вы думаете, пройдет?
Зная то, как ваша команда умеет запихивать все, конечно:)
Количество делителей — это уже очень много. Примерно 10^5. Мое решение делает 3*10^4 итераций на тест.
А почему решение №2 задачи C — это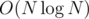 ? Вроде же O(N), у нас 2N событий и 2 прохода.
? Вроде же O(N), у нас 2N событий и 2 прохода.
А отсортировать?
А, ну да.
данные на входе уже отсортированы. и если делать события не в лоб, то сложность будет O(N)
Что сортировать? Данные уже на вход отсортированные даются. У меня чистый O(N). Линейно двигаю отрезок по циклу при помощи метода 2 указателей.
а сортировка?
ну их еще упорядочить надо. события то. хотя, можно их сливанием упорядоченных массивов посортить... тогда будет O(N). но зачем усложнять себе жизнь?
Ну я, например, решал с помощью двух указателей. Хотя алгоритмически это то же самое, что и слияние, только результат нигде не хранится. Преимущество в том, что не нужно создавать отдельные объекты для событий.
да, указателями тоже можно. когда я писал комментарий, идеи с указателями мне в голову не приходило (в том числе и из других комментариев).
я лично решал сортировкой событий за NlogN.
К сожалению, нет время описывать подробно. Мое решение вроде как O(N): http://mirror.codeforces.com/contest/163/submission/1414357 Мне казалось, что все так решали и не надо никаких O(NlogN)... :)
In problem B " So we need to make log (10^27) = 90 iterations " where from 10^27 came ?.....i just want to know how you concluded that 75 iterations will be enough.
You have a range of doubles [0, 1e9] and two doubles here are considered "equal" if their substraction is less than 1e-18. Then you actually have 1e27 "different" double values, don't you?
На мой взгляд, разбор задачи B (про леммингов) не полон.
Максимальный ответ равен 10^9, а расстояние между оптимальным ответом и следующим за ним не меньше 10^-18. Таким образом, если у вы используете числа с как минимум 27 десятичными знаками относительной точности, можно делать 90 итераций и быть спокойным...
На контесте я сдал (на ACC) решение с double (16 десятичных знаков относительной точности) и очень боялся, что оно упадет по точности. Очень странно, что рассуждения на тему ТОЧНОСТИ (а не количества итераций) отсутствуют в разборе жюри.
Как я понимаю, нужно доказать, что если оптимальный ответ равен A, а какой-то другой ответ равен B, то |B-A|/A >= 10^-16. Если это неверно, то многие засчитанные решения (в том числе мое) могут быть убиты хаком.
Вообще, подобное рассуждение в контест напугало меня настолько, что я придумал неправильное "точное" решение и отправил его.
А вот как на самом деле. Ответом может быть некоторая дробь j/v[i], 1 <= j <= k. Параметр h вообще в задаче лишний, примем его за единицу. Пусть у нас есть i1/v1 и i2/v2 как возможные ответы задачи. Относительное отличие 1 - (v1/v2)*(i2/i1). Тогда, если взять i1 = A, i2 = A+D, v1 = B-C, v2 = B, получим 1 - ((1-C/B)*(1+D/A)) = C/B-D/A+(CD)/(AB), что, вроде, положительным меньше 10^(-9)*10^(-5)=10^(-14) не бывает.
А я правильно понимаю, что среди стандартных в С такого типа не предусмотрено? В доках GCC __float128 обзывают гнутым расширением.
Да, такого типа в большинстве языков нет.
Но это теперь неважно, поскольку I_love_natalia уже показал, что достаточно 14 десятичных знаков относительной точности, то есть обычного double хватает=)
А можно более подробно как-нибудь описать решение первой задачи. А то, что-то не совсем доходит какая там динамика. f[i][j] — количество пар подстрок что строка S начинается с позиции i а строка T, не сильно понимаю. (Заранее благодарен).
Попробую(правда, у меня слегка другое решение). Итак, пусть f[i][j] = число равных пар "подстрока-подпоследовательность" таких, что подстрока закончилась ровно в символе i, подпоследовательность закончилась не правее символа j. (Всё инициализируется нулями). Тогда:
1)s[i] != t[j]
f[i][j] = f[i][j — 1] (поскольку ясно, что сделать иначе мы не можем)
2)s[i] == t[j]
f[i][j] = (f[i][j — 1] + 1 + f[i — 1][j — 1]) % MOD
(первое слагаемое — см. случай 1, второе слагаемое — новые подстрока и подпоследовательность длины 1, третье слагаемое — возьмём все "старые" пары и припишем новый символ).
Как "собрать" ответ? Очевидно, что искомые подстроки заканчиваются на любом символе, а подпоследовательности — гарантированно не правее, чем на самом правом сиволе. Таким образом,
for(int i = 0; i < n; i++){
ans += f[i][m — 1];
ans %= MOD; }
А будет разбор задач для Div.2?
Врядли
Прикольно. Обычный рейтинговый контест — а разбора не будет? Не в духе codeforces.
Они даже для Testing Round делают разборы)
думаю для А и В (Div2) вполне достаточно посмотреть решения других участников.
А что тут разбирать та? A) отсортировать массив и вывести h[n — a] + h[n — a — 1]; B) пройтись по цифрам числа а и пытаться жадно увеличить каждую цифру.
ПС: Получил на бинпоске по С WA, когда сделал 100 итерации получил АС, вместо того чтобы стать фиолетовым, стал зеленым Т_Т
Может быть, но точно не от меня :-) Я даже условий не читал.
please help!! i tried to submit my solution to the problem E many times, but my solution couldn't be received. the screen says "Ooops! Something has broken down in Codeforces. Do not panic, you can try to reload the page or return Home. Anyway we will carefully read megabytes of logs, analyze stacktraces and fix the problem.". i tried submitting a empty-code to it,and the code was received(of course, wrong answer). and i tried log-out and log-in,but the situation didn't improve. ??why?? my code is no compile-error, or memory limit exeed. also, i tried the custom test,and the custom test was no problem.
thank you for fixing the problem ^_^ my cause of trouble is using the "%lld". now,the program doesn't be received,too,however,the screen told me a proper warning.
Мой ответ на тест задачи В циферка в циферку похож на ответы тех, у кого полное решение, но почему-то мой не проходит. Как так может быть?
В чем-то разница точно есть ;-)
Возможно, ответы даны с символом "..." посередине. Значит, часть пропущена. Возможно, ошибка именно там.
Could someone explain me, why mathematicaly 90 iterations is enough for 163B — Lemmings? I have done a solution with 40
can someone please elaborate the dp states and transition of A.
In problem 163A - Substring and Subsequence, should the formula for
Answerbe the summation overioff[i,|t|]instead off[i,0]? 39291217Update: The answer is NO! The editorial code reverses the direction of the
jloop, and the original formula is correct.Why is the time limit so tight for E problem, I tried a suffix array approach and a lazy segtree to maintain the contributions, but got TLE at testcase 4.
did you solve it
I came up with a nlogn solution, but didn't pass.
280142173