Hi Codeforces Community,
I recently learnt about segment trees and enjoyed it a lot. Right now, I am trying to solve a problem http://www.spoj.com/problems/MKTHNUM/.
The approach I used was to build the segment tree but maintain a sorted array at each segment. Afterwards, for each query [L, R], I got all the disjoint segments that form [L, R] and merged them recursively in order to answer query. I realize that there is a faster way to answer each query in lgn, (lgn)^2 times. I also think it is related with persistent segment tree.
I have tried to access Anudeep's tutorial on it but it is not loading. Please can someone help with an example or idea of how Persistent segment trees work?
Thank you.
So far, I have seen this http://mirror.codeforces.com/blog/entry/15324, http://e-maxx.ru/algo/segment_tree and Anudeep's blog just opened.
It explains building a segment tree for each segment. What does this even mean? I know how to build a straight -forwards segment tree but how does this translate to building a segment tree on each segment.
An example or two will do for me.
Thank you.
The approach was also mentioned in this blog post by PrinceOfPersia. Perhaps it might help :)
(PS. I don't how to do it yet. I was also having issues understanding these tutorials.)
I came to a solution with O(log3N) complexity.
After you have found all disjoint intervals for a request (there will be not more that O(logN) intervals), use binary search to find the value of k-th element.
Total complexity will be O(Qlog3N), where Q — number of requests.
UPD Here you can find discussion about solution with persistent segment tree in Russian.
Thank you. I realize that there will be O(lgn) intervals all disjoint. In addition, we don't have access to all of them at the same time. So we are left with merging the segments 2 at a time till we have our answer.
Suppose the problem is to use binary search to find Kth element in a group of sorted disjoint segments, how can we do this.?
What we can do — for a request return nodes (segments in a tree) that make up the request interval (for example, a vector).
Then in order to find k-th element just use binary search of a value for every segment: if current value is greater than ai elements of segment i and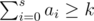
then try a value less, otherwise greater. This works in O(log3N) time — logN searches for value in logN arrays with logN complexity.