632A - Бабушка Лаура и яблоки
Задача предложена пользователем unprost.
Рассмотрим на процесс с конца. Последний покупатель всегда покупает половину яблока и половину получает бесплатно (поэтому последняя строка на самом деле всегда равна halfplus). Далее каждый покупатель удваивает текущее количество яблок и возможно прибавляет к нему единицу. Таким образом, нам просто задано бинарное представление числа записанное с конца. Для подсчёта ответа нужно просто с конца восстанавливать количество яблок попутно, вычисляя сумму денег.
С++ solution by me.
С++ solution by unprost.
Сложность: O(p).
632B - Алиса, Боб, две команды
Задача предложена пользователем Lewin Gan Lewin.
Посчитаем частичные суммы на префиксах отдельно для всех чисел (в массиве s1) и отдельно для чисел напротив, которых стоит буква B (в массиве s2). Теперь мы можем за O(1) вычислять сумму на любом подотрезке, а также сумму на любом отрезке по числам напротив буквы B.
Переберем теперь префикс или суффикс и посчитаем сумму в случае его изменения по формуле: sum(s1, 0, n - 1) + sum(s2, 0, i) - 2·sum(s1, 0, i) для префикса и sum(s1, 0, n - 1) + sum(s2, i, n - 1) - 2·sum(s1, i, n - 1) для суффикса.
C++ solution by me.
Python solution by Lewin.
Сложность: O(n).
632C - Наименьшая конкатенация строк
Задача предложена пользователем Lewin Gan Lewin. Доказательство транзитивности также принадлежит ему.
Отсортируем все строки по компаратору a + b < b + a и сконкатенируем их в получившемся порядке. Докажем, что ответ оптимальный. Пусть эта операция транзитивна (то есть из 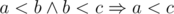 ). Рассмотрим оптимальный ответ в котором есть пара строк, находящихся по этому отношению в обратном порядке. Поскольку это отношение транзитивно, то без потери общности можно считать, что это пара соседних строк. Но тогда мы их можем просто поменять местами и улучшить ответ.
). Рассмотрим оптимальный ответ в котором есть пара строк, находящихся по этому отношению в обратном порядке. Поскольку это отношение транзитивно, то без потери общности можно считать, что это пара соседних строк. Но тогда мы их можем просто поменять местами и улучшить ответ.
Докажем транзитивность отношения. Будем смотреть на эти строки как на числа в 26-ной системе счисления. Тогда отношения a + b < b + a эквивалентно 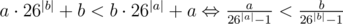 . Последнее есть просто отношение для действительных чисел. Таким образом, мы доказали транзитивность отношения a + b < b + a.
. Последнее есть просто отношение для действительных чисел. Таким образом, мы доказали транзитивность отношения a + b < b + a.
C++ solution by me.
Python solution by Lewin.
Сложность: O(nLlogn), где L — наибольшая длина строки.
632D - Самая длинная подпоследовательность
Задачу предложил Денис Безруков pitfall.
Пусть cntx количество повторений числа x в заданном массиве (понятно, что числа большие m можно не рассматривать). Переберём  и 1 ≤ k, x·k ≤ m и увеличим значение в позиции k·x в некотором массиве z на величину cntx. Таким образом, значение zl равно количеству чисел в исходном массиве делящих l. Найдём минимальное l с максимальным значением zl (1 ≤ l ≤ m). Легко видеть, что ответом на задачу будут числа делящие l.
и 1 ≤ k, x·k ≤ m и увеличим значение в позиции k·x в некотором массиве z на величину cntx. Таким образом, значение zl равно количеству чисел в исходном массиве делящих l. Найдём минимальное l с максимальным значением zl (1 ≤ l ≤ m). Легко видеть, что ответом на задачу будут числа делящие l.
Оценим время работы решения. Количество пар (k, x) можно сверху оценить как 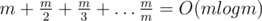 .
.
C++ solution by me.
Java solution by pitfall.
Сложность: O(n + mlogm).
632E - Вор в магазине
Задачу предложил Алексей Чесноков CleRIC.
Пусть k = 2, тогда это стандартная задача которая может быть решена с помощью БПФ (быстрого преобразования Фурье). А решается она следующим образом: рассмотрим многочлен в которого коэффициент при i-й степени равен единице если и только если в заданном массиве есть число i. Возведём этот многочлен в квадрат, тогда те i коэффициент при которых в квадрате не равен 0 будут находиться в ответе. Легко обобщить это решение на случай произвольного k. Нужно просто исходный многочлен возвести в k-ю степень. Это, конечно, нужно сделать с помощью бинарного возведения в степень. Сложность получается O(WlogWlogk), где W — максимальная сумма.
Заметим, что это решение можно улучшить. Зачем возводить в степень многочлен, когда можно возводить в степень его образ (то есть его ДПФ)? Единственное, что нас может остановить это то, что в случае комплексного БПФ будут получаться очень большие числа (порядка 1000-х степеней) и соответственно никакие вещественные типа нас не спасут). Но это можно сделать в целых числах используя теоретикочисловое преобразование Фурье (ТПФ). У этого решения есть проблема, что при преобразовании (прямом или обратном) какие-то коэффициенты могут случайно обнулиться по модулю простого из ТПФ, но на самом деле коэффициент не ноль. Это можно обойти случайным выбором простого (а лучше двух или трёх), чтобы никто не мог взломать решение. Таким образом, получаем сложность O(W(logW + logk)).
Основное авторское решение было со сложностью O(WlogWlogk) с комплексным Фурье, второе с той же сложностью но по модулю, третье было с улучшенной асимптотикой (решение уже взломано Андреем Халявиным halyavin).
С++ solution, complex FFT by me.
С++ solution, NTT by me.
С++ solution, improved NTT by me.
С++ solution by CleRIC.
P.S.: Чтобы решение было быстрым нужно каждый раз умножать многочлены нужной степени, а не степени 220.
Сложность: O(WlogWlogk) или O(W(logW + logk)), в зависимости от смелости кодера :-)
UPD: Оказывается первый подход тоже имеет сложность O(W(logW + logk)). Смотри ниже комментарий пользователя halyavin.
632F - Волшебная матрица
Задача предложена пользователем Lewin Gan Lewin. Решение и доказательство также принадлежат ему.
Рассмотрим полный граф с весами рёбер aij. Обозначим Bij — минимальное значение максимального ребра на пути из вершины i в вершину j. Очевидно aij ≥ Bij по определение Bij.
Если матрица волшебная мы можем выбрать произвольную последовательность k1, k2, ..., km и получить aij ≤ max{ai, k1, ak1, k2, ..., akm, j} (для этого нужно последовательно применить третье неравенство для волшебной матрицы). Также легко показать, что если это условие выполнено, то матрицы волшебная (нужно просто взять m = 1 и выбрать произвольное k1).
Таким образом, мы получили, что матрица волшебная тогда и только тогда, когда aij ≤ Bij. Пользуясь неравенством aij ≥ Bij окончательно получаем ai, j = Bi, j.
Теперь нам нужно быстрый способ подсчёта значений Bij для всех пар (i, j). Это можно сделать вычислым MST (минимальное покрывающее дерево графа), поскольку MST минимизирует максимальное ребро на путях между всеми парами вершин. Таким образом, решение выглядит следующим образом: сначала нужно найти MST (например, алгоритмом Прима за O(n2)), а затем нужно найти наибольшее ребро на пути из i в j и проверить, что оно равно aij (я это делал с помощью бинарного подъёма по дереву, но это можно делать во время построения MST). И, конечно, нужно не забыть предварительно проверить матрицу на симметричность и нули на диагонали.
P.S.: К сожалению в этой задаче мы не могли увеличить n, поскольку тесты здесь очень специфические (и уже имели размер порядка 67MB) и генератором их задавать было нельзя. Большинство решений, которые сдали участники на контесте использует bitset-ы и работает за 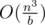 , где b = 32 или b = 64.
, где b = 32 или b = 64.
C++ solution, binary lifts by me.
Java solution by Lewin.
Сложность: O(n2logn) или O(n2).











В задаче C авторское решение на cpp долго складывает строки(за квадрат?) http://mirror.codeforces.com/contest/632/submission/16455324
спойлер
Ого. Больше не буду использовать accumulate. А почему так? Там типо каждый раз он создаёт новую строку?
ну он в цикле вызывает что-то типа a = a + b
оптимизировать до a += b компилятор в общем случае не имеет права, а для строк видимо не догадывается
You can remove the symmetric condition from the problem. In particular, by taking k = i, we get that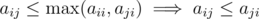 , as aii = 0. Similarly, aji ≤ aij, so aij = aji.
, as aii = 0. Similarly, aji ≤ aij, so aij = aji.
I'm curious. Does there exist an efficient solution to this problem if the condition is instead: aij ≤ aik + akj?
It seems you can simply run Floyd algorithm and check that the matrix remains the same.
But the solution will be O(N^3) then. I think he asked if there is a solution for the same size of the data ( O(N^2*log(N)) or better).
are you planning to write intended solutions for the other problems?
Another approach to F is that set of all edges that are less than any fixed constant is transitively closed. This property can be checked by filling the graph starting from shortest edges. Once all edges of the same length are added we need to check that all connected components are full graphs. We can compare the number of added edges and the sizes of connected components to do that.
what about editorial for problem D?
It's ready.
If you use the minimum power-of-two size instead of 2^20 in the problem E, you will get only O(W*log(W)) because time complexity of all multiplication steps except the last one doesn't matter since steps time complexity decreases exponentially. The i-th step, if you count from the end, will only work with the data of size W/2^i.
Nice! I'll update the editorial.
beautiful proof for C. keep the educational rounds coming : )
I also think so. Thanks to Lewin for that beautiful proof!
So are you saying the first model solution is incorrect? Either way, you could also choose to clean up the vector after each multiplication (map each element x to sign(x)), this seems to work fairly well: 16472285
We will have precision problems only for improved solution. Of course model solution is correct and there are no precision problems for the first approach.
In problem C I don't get it why we can assume that pair of strings are neighboring because of the transitivity?
Please somebody helps me !!!
We just assume that the answer is S = s[1].s[2].s[3]....s[n](some string) in this case by the approach of proving from the opposite there are exist i and j that i < j and s[i].s[j] > s[i].s[j] then we can chech i and i+1 if there is alright then i+1 and i+2 and so on until we reach j.
can anyone explain logic behind 16447028 submission?
First, it is taking out the lowest value 'mn' from all the ai's .
Let , somehow we get to some PSEUDO total cost 'i' by using these modified ai values. and also, we used y slots out of the original k slots. [the order does not matter] here , y <= k . So , we can get to an ACTUAL total cost if we add 'mn' in ALL the 'k' slots. [in ALL 'k' slots, not only in the remaining k-y slots] The new ACTUAL total cost = i + mn*k ;
Here, The dp[i] means , to get to this PSEUDO total cost value 'i' , we can use MINIMUM dp[i] slots of out k slots. That is dp[i] is minimum 'y' of possible 'y's .
There may be a confusion , why we are working with the smallest one. Its because if we choose any other ai , then after subtraction some 'ai' values will get negative which is not acceptable.
Another point is that, it may seem that we are using 'mn' in every slot. But actually this is not the case. We have already done a subtraction.
I hope it helps.
You just translated code into words. Though my question was about proof of correctness of the mentioned submission. I am sorry, but you did not provide the proof.
It's a solution with complexity O(n*m*max(a)) = O(10^9).
He calculates dp[x] = the minimum objects with price a[i] — min a[i] that the thief need so that the total costs is x.
If dp[x] <= k, he can add as much product with price a[i] min — min a[i] = 0 as he needs in order to fill the bag with k products.
But the main problem here is he calculated with the formula use too much time. You can read in the code and see it.
Also found a simple dp solution for Problem E. 16454858 by yummy
Can you please explain this solution with a bit more detail? I am not really familiar with FFT concepts so it will be really helpful if you can explain the dp solution.
This comment may help .
I got the basic gist of the solution but one thing that we need to subtract min cost out of each cost when in the end we are adding it again to get final result?
That is right. If we consider a possible final combination with some modified ai values , then all we have to do is to add that 'minimum' in each of the 'k' slots.
What I am asking here is that, why is it necessary to subtract the min element? Can we do it without subtracting any element?
No we can't do without subtracting minimum element. Once we subtracted the minimum element, we reduce problem to a case where one number equals to zero. If one number equals to zero, the problem can be changed to require less than or equal to k numbers in the sum instead of exactly k numbers in the sum. This allows us to use dynamics where we store for each sum the minimum amount of numbers to get it.
Thanks @halyavin. I solved the question. But still I have one concern about its complexity. The complexity of solution as explained in editorial is O(akn).I also found the same complexity. This seems to be of the order of 10^9 . Isn't it too high to pass? How do we decide if some complexity is perfect for given time limit?
You are correct, it is 10^9. But the TL is 5 seconds for this problem, so it turned out to be ok. I think the reason this solution works so well is its cache-friendliness: it accesses dynamic programming array consequently although in 2 places up to |a| elements apart.
In general, it is hard to predict solution runtime even for me. I try to estimate cache-friendliness, complexity of operations in the algorithm and the likelihood that I found the author solution but I still regularly end up quite far from the real runtime. Luckily, it doesn't always matters — if you found only one solution, there is no downside in trying it.
I think that C isn't fully proved. Suppose we sorted the strings using the comparator and have a subarray s[i]...s[j] (i < j), such that s[i] = s[i + 1] = ... = s[j], where s[i] = s[j] means s[i]s[j] = s[j]s[i]. Then we need to prove that, whichever permutation of the subarray we take we will get the same concatenation.
Can someone explain why
?
Never mind, proved it myself. m+m/2+m/3+...+m/m = m(1+1/2+1/3+...+1/m). Expression in brackets is harmonic series, which is O(log m), so totally we get O(m log m)
In problem A :
Complexity:
O(n),O(p)incorrect!!Can anyone explain DP solution of problem E. Thanks in advance:)
Problem $$$F$$$ can be solved with bitsets too 160770914. Add the elements in matrix in increasing order (i.e. mark with $$$1$$$ bit) and check if $$$arr[i]$$$ & $$$arr[j]$$$ has any set bits.