Чуть раньше закончился раунд опенкапа, предлагаю обсудить задачи здесь.
Как решать B и I?
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Чуть раньше закончился раунд опенкапа, предлагаю обсудить задачи здесь.
Как решать B и I?
| Название |
|---|



I: заметим, что сумма модулей может раскрыться 16 различными способами, тогда будем хранить 16 максимумов вида ±x1±x2±x3±x4 и пытаться релаксировать ответ только с ними.
Я правильно понимаю, что в общем случае при переходе от манхеттенского расстояния к расстоянию Чебышёва, переход будет обязательно из пространства размерности n в пространство размерности 2n - 1? А расстояние Чебышёва сводится к манхеттенскому?
Можешь подробнее рассказать?
|x1 - y1| + |x2 - y2| + |x3 - y3| + |x4 - y4| можно раскрыть 24 способами за счёт домножения или не домножения на - 1 каждого из слагаемых. Для зафиксированного способа раскрытия нужно знать вектор, который максимизирует вклад x с учётом коэффицентов раскрытия. Вектор, который максимизирует раскрытие не обязательно будет раскрываться именно так с вектором y, но это не беда, так как мы можем сделать вывод, что при другом раскрытии он даст ещё больший вклад.
Ок, спасибо
B: динамика по профилю + двоичное возведение матрицы в степень. Пусть dp[n][up][down] — сколько есть способов заполнить первые n ячеек, чтобы сверху и снизу остались незаполненные суффиксы размера up и down, где up, down ≤ 9. Замечаем, что dp[n][i][j] есть линейная комбинация чисел из dp[n - 1] (коэффиценты для каждого случая предлагаю найти самостоятельно). Записываем эти линейные комбинации в матрицу и возводим её в нужную степень.
Как решается F?
Пусть gcd = p1a1p2a2...pnan, lcm = p1b1p2b2...pnbn. Каждое простое число будем рассматривать отдельно. Пусть ai < bi. Тогда мы можем распределить его по k числам (bi - ai + 1)k - 2(bi - ai)k + (bi - ai - 1)k. Все эти величины перемножаются по различным простым числам.
То есть, разбиение gcd и lcm на простые фактически задаёт нам точные минимумы и максимумы вхождений всех простых, которые делят наше множество чисел. Минимум и максимум должны строго достигаться, что можно учесть при помощи формулы включений-исключений, которую я написал выше.
Здравствуйте! Вы не подскажете, почему такая формула? Заранее спасибо за ответ!
Пусть степень вхождения простого p в LCM равна b, а в GCD равна a.
Чтобы удовлетворить данное условие необходимо, чтобы у каждого числа степень вхождения лежала в отрезке [a, b] и при этом, существовали числа у которых эта степень строго равна a и b соответственно. Тогда количество способов распределить простые в этих числах есть: 0 — если b < a, 1 — если b = a, или (b - a + 1)n - 2(b - a)n + (b - a - 1)n — если b > a.
Ответ это произведение соответствующих величин по всем простым.
Как решать L?
Утв. 1 Пусть a <(=/>) b тогда c <(=/>) d
Утв.2 Пусть b — a = 2^k * x , x -нечетно, тогда d — c кратно x
Теперь решение для случая a < b(a > b симметрично, a = b вообще просто(но можно и прикрутить к одному из этих случаев):
Сперва уменьшим максимально разницу (будем делить ее на 2, пока не станет x). Это можно делать как в двоичном возведении в сетпень — если оба числа четные, делим сразу, если оба нечетные — добавляем 1 и делим. После этого нужно получить из пары (a', b') пару (1б 1 + x). Для этого будем уменьшать a' похожим образом,, из (a', b') получаем (b', b' + x). из этого (a', b' + x), а это делим попалам (либо +! и делим пополам).
Теперь из (1, 1 + x) нужно получить (c, d). Сперва нарастим разницу до d — c. Это можно делать операциями вида (1, 1 + kx) за x раз переходит в (1 + x, 1 + (k + 1)x), операцией третьего тпиа получаем (1, 1 + (k + 1)x). По утверждению, разница имеет вид kx, так что мы ее получим. дальше тупо добавляем по 1. (c — 1 раз)
Считаем что a < b и c < d, пусть l = b - a, получим из пары (a, b), пару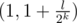 , где k степень вхождения двойки в l.
, где k степень вхождения двойки в l.
Сначала сделаем a и b разной четности, проводя операции первого и второго вида. Потом превратим a в единицу операциями вида: (a, a + x) -> (a + x, a + 2x) -> (a, a + 2x) -> (a / 2, a / 2 + x), если a четное или (a, a + x) -> (a + x, a + 2x) -> (a, a + 2x) -> (a + 1, a + 2x + 1) -> ((a + 1) / 2, (a + 1) / 2 + x), если нечетное.
Теперь мы можем получить (c, d) из (1, 1 + v) только если d - c делится на v. Этого можно добиться получив из (1, 1 + v) все пары (i, i + v) потом объединив нужные нам пары.
Замечу, что подобная задача на Yes/No уже имела место быть: 271E - Три коня.
Как решать D и K?
В K сдал следующее (доказываеть, что если у меня NO, то действительно NO не умею).
Заметим, что операция обратима. Значит надо привести к некоторому каноническому виду обе строки, и сравнить, что получлось одно и тоже. В качестве канонического вида, у меня получилось следующее: "сколько-то нулей" "1 единица" "остальные нули" "остальные единицы" . К такому виду приводится методом, берем самый правый 0, если левее него есть хотя бы 2 единицы, то переворачиваем отрезок с началом во второй 1 и концом в этом 0. Количество единиц в конце увеличилось на 1, значит будет не более N итераций. Итого N2 времени и 2N операций всего. Остается только вопрос, почему оставшуюся единицу нельзя передвинуть. Мы с pashka решили, что это звучит достаточно правдопобно, чтобы сесть и написать, но было бы интересно узнать.
x1-x2+x3-x4+... — это инвариант, где x1,x2, и так далее — это позиции единиц в возрастающем порядке.
(Из разбора) Назовём нолик чётным/нечётным, если разность числа единиц слева и справа от него чётна или нечётна соответственно. Утверждается, что чётность или нечётность каждого нолика (как помеченного, то есть передвигающегося по полоске) не меняется.
Действительно, посмотрим на нолик, попавший в переворачиваемый отрезок. Единицы вне нашего отрезка никак не влияют, а единицы из отрезка изменят разность на чётное число: если до операции слева от нолика было l единиц, а справа r единиц из данного отрезка, то после они поменяются местами, то есть разность изменится на (r - l) - (l - r) = 2(r - l).
Так как чётность каждого нолика постоянна, то количество нечётных ноликов — инвариант. Но легко видеть, что у разных "нормальных форм" она разная.
Количество 0, слева от которых четное число единиц — инвариант. На основе этого факта строится линейное решение — считаем этот инвариант за один проход, параллельно перекидывая нули в начало (до или после первой единицы в зависимости от четности).
Solved by my team mate.
D: It is somewhat greedy. Every time, you will shift K apples by 1km. Now in that time, you will pay the necessary amount of apples, or even you might need to ignore (it is not worth to go back 1km for 1apple). So you can move apples by 1km in O(1). The problem is L is too big. So we can't run O(L) algorithm. Let's look at other parameters. How about K? If K is too small, then you need to pay apples quite frequently. And you will notice that, for reasonable small amount of K, you can't move apples much further. What about big K? Well.. in such case, 'number of rounds' you need to shift all N apples is same for quite a few km. So you need to derive some formula / clever code to do these transferring in a "batch".
Как решать Е? Писали разбор различных случаев, но упорно получали WA2. С помощью ассертов вроде поняли, что тест 2 — тот случай, когда прямая, на которой находятся две точки (станции), не пересекает или касается окружности (кратера). Написали тернарник, который ищет оптимальную точку на окружности для способа размещения дорожки точка — окружность — точка, сравнили со способами окружность — точка — точка, но все равно WA2.
Есть еще вариант
Мы задавали клар по этому случаю, нам ответили "без комментариев". Для меня этот случай представляет собой "сеть дорожек", а не "дорожку".
Плюсую, это место в условии написано очень плохо, как будто специально хотели запутать. То, что не ответили на клару и не заброадкастили ответ — вообще полйный бред.
Тогда это уже вопрос к жюри — толкование слова "дорожка". Мы писали сообщение жюри с таким вопросом: "Может ли дорожка состоять из трех отрезков с началом в одной точке?" через два с половиной часа после начала контеста, повторили его на английском еще через час и только через четыре часа после начала контеста получили ответы на оба вопроса — "Без комментариев" и "No comments". ИМХО, самый очевидный математический аналог понятия "дорожка" — это "кривая", что исключает такую возможность. Мы все-таки задали вопрос, может ли быть не кривая (скорее "на всякий случай"), и как минимум печально, что ответ на этот вопрос поступил с такой большой задержкой, даже если вопрос не совсем корректный.
UPD: оказывается, сокомандник уже отписался.
Аналогично, на мой вопрос "возможна ли непрямая(к примеру, дугообразная) дорожка?" получил "No comments".
Мое виденье этой задачи (тоже получаю WA2):
В случае если обе станции лежат на окружности кратера дорожка идёт вокруг окружности до точек. Представим её как такую ломанную из подотрезков. Чем мельче отрезки поворотов ломаной дорожки тем меньше её длина. Соответственно минимальной длиной будет длина дуги на окружности между точками (R*a, где a это радианный угол). Всё это верно если допустимы непрямые дорожки, допустима дорожка "на границе", допустима дорожка из нескольких поддорожек. Если неверно последнее, ситуация "обе точки на кратере" не имеет решения что не оговорено в условиях. Если неверно предположение что дорожка может идти по границе кратера то непонятно, откуда нам выдумать o(1) — отступ от этой дорожки. Если неверно что дорожка может быть непрямой то получается что истинный ответ запрещён условиями.
В случае если хотя бы одна из точек не находится на границе кратера, нужно построить две прямые: к окружности кратера от ближайшей станции и между ними. Соответсвенно получаем abs(A-B) + min(abs(A-O),abs(B-O)) — R. (конкретно моя реализация была на комплексных числах, там в C++ точно такой код).
Как решается H?
С помощью трипа по неявному очевидно как решать, но существуют ли решения за O(n)?
Заметим (докажем?), что после любой операции строка сдвигается циклически на какое-то количество символов и может реверснуться. Тогда очевидно, что нам важно знать после всех операций: где окажется первый символ и где окажется второй символ (для определения направления строки). Для них собственно будем моделировать процесс в лоб. Ну и имея их позиции в итоговой строке ответ восстанавливается легко.
это messenger которая? там есть решение за O(n). Мы решили ее так. Сначала заметим, что после любой комбинации инвертирования мы сможем прочитать изначальное слово целиком, следуя влево или вправо от первого символа. таким образом необходимо только посчитать позицию первого символа pos после каждого X[i]. Если pos < x, то pos = x — pos — 1, иначе pos = k + (x — pos) — 1. А дальше заполняем ответ. Если n % 2 == 2, то ans[(pos + i) % k] = s[i], иначе ans[(pos — i)] = s[i]
Выложил контест на тренировки.
Здорово! А можно еще и другие также выложить? У меня нету возможности писать контесты и доступа нет. Но, хотелось бы порешать задачи.
Те ICL контесты, что делались на полигоне — можно. Остальные теоретически тоже, но это не быстро и, если честно, не вижу в этом смысла.
дать возможностьрешать задачи тем участникам, для которых закрытодорешованиею