zloyplace35's blog

Codeforces Round #368 (Div.2) разбор
By zloyplace35, 8 years ago, translation, In English

Thanks all participants. I hope, you liked problems.

A — Brain's photos

We need to do exactly what is written in the task: to consider all of the characters, and, if there is at least one of the set {C, M, Y} print "#Color" else — "#Black&White"

B — Bakery

Note that it makes no sense to choose the city for bakeries and the city with the warehouse so that had more than one way between them, as every road increases the distance over which you have to pay.

So, the problem reduces to the following: select two neighboring cities so that one is a warehouse, and in the other & mdash; no. For doing this, simply iterate through all the city with the warehouse, among the neighbors of each town without looking for a warehouse and update the answer. If there is such a pair of cities, print -1.

C — Pythagorean triples

D — Persistence bookcase

Solution №1:

Note that the data is delivered all at once (offline). Then we can build a tree of versions, then run out of the DFS root and honestly handle each request in the transition from the top to the top.

Solution №2:

Note that Alina uses operations that relate to the columns. We can make an array of versions of the shelves, and each version of the cabinet to provide an array of indices and the corresponding shelves to store it explicitly. Then, for the operation, such as changing wardrobe, shelves, a new version which has been changed, this version of the index is recorded on the same shelf position. This approach eliminates the decision on the use of extra memory for storing unnecessary information.

E — Garlands

Let us handle each request as follows:

Let's go for a "frame" request and remember lamp garlands, which lies on the boundary. Then, in order to find concrete garland, what part of it lies within the query, sum all of its segments, the ends of it are lamps that lie on the "frame".

Also, do not forget the garland wich lies entirely within the request. Each garland at the beginning we find the extreme points, and to check whether it lies entirely within the query, check whether the lie inside its extreme points.

  • Vote: I like it
  • -2
  • Vote: I do not like it

Comments Comments (71)
| Write comment?
»
8 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Can you please give the tutorial for Problem C — Pythagorean Triples?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +16 Vote: I do not like it

    n = 1, 2: There are no solutions (easy to prove)

    n is even: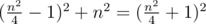

    n is odd: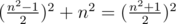

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Do you have a proof for the formula ?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        You can prove it by induction.. Check the base case by considering the case that sum of two sides of triangle is greater than the third side. This will give you n>1 for odd 'n' and n>2 for even 'n'.

        → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        You can directly substitute and check using (a + b)2 = a2 + b2 + 2ab formula.

        No need of induction.

        For instance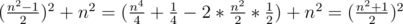

        → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      how can i come with such a formula if i didn't know it before ?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it +2 Vote: I do not like it

        Actually you can figure it out easily. You see that n²=m²-k²=(m-k)×(m+k), so you need to find a way to present n² as a×b with (a-b) is even. You will always find a and b if n is odd and larger than 1, which is 1 and n². If n is even and n is larger than 2 then how about 2 and n²/2. Easy as that, huh?

        → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
        ← Rev. 2   Vote: I like it +1 Vote: I do not like it

        http://mirror.codeforces.com/blog/entry/46681 explains it.

        → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        The second formula for odd numbers is easier to see in the following form —

        (k)^2 + (2k + 1) = (k + 1)^2

        If n is odd, it's square is also odd ... so** n^2 = 2k + 1**, and the equation is re-written in terms of n.

        If n is even ... i.e.** n = 2m**, then** n^2** is also even ... so n^2 = 4k .. a multiple of 4. Using that observation,

        then

        (k — 1)^2 + (4k) = (k + 1)^2

        Again the equation is re-written in terms of** n**.

        → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +19 Vote: I do not like it

    consider a^2 = b^2 + c^2 (PT)

    now we are given the cathetus (any of the two sides other than hypotenuse) let c = n then -> n^2 = (a-b)*(a*b) [a^2 — b^2]

    check yourself that either (a-b) and (a+b) both are even else both are odd

    from the above eqn (a-b) and (a+b) are factors of n^2

    simplest -> if n is odd let (a-b)=1 and (a+b)=n^2

    if n is even let (a-b)=2 and (a+b)=n^2/2

    solve these and u will get values for a and b :) but for n<=2 no ans exists so print -1 :)

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Brilliant explanation .

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      why did you assume that if n is odd you put a-b =1 why 1 not any odd number .and the same if n is even ?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I said that's the simplest.... Plus u need a-b to be a factor of n^2 and 1 is a factor of every number that's why a-b=1 same goes if n^2 is even

        → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Your_dad, actually we are given either cathetus or hypotenuse. Is there always exist a Pythagorean triple in which given n represent cathetus? How can we prove that?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Let n = 2k where k > 1. Consider the Pythagorean triple obtained by scaling (3, 4, 5) by .

        Now suppose n has some odd prime factor. Every odd prime p is the difference of two consecutive squares. Let x be such that (x + 1)2 - x2 = 2x + 1 = p. Thus, (p, 2x(x + 1), x2 + (x + 1)2) is a Pythagorean triple. Scale it by and you obtain a triple that has n as a cathetus.

        Thus, every integer n > 2 is a cathetus of at least one right triangle.

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          How to prove that for n <= 10^9 and n is a cathetus, there exists c <= 10^18 where n^2 + x^2 = c^2?

          → Reply
          • »
            »
            »
            »
            »
            »
            8 years ago, # ^ |
            ← Rev. 2   Vote: I like it 0 Vote: I do not like it

            For the case of 2k, it's trivial, so suppose n has an odd prime factor p = 2x + 1 as in my previous comment. We can show that my scaled right triangle will be small enough for the problem:

            As for the hypotenuse:

            Note that in the last step, the reason $x+2 \leq p$ is because x ≥ 1 since p is at least 3.

            → Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    [http://www.codeforces.com/blog/entry/46681] try this:P

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Hi
    You could refer this explanation. :D

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem D solution no.1

Does that mean if there's op is '4', then the tree contains a cycle?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    No. in the case of 4 x , you don't attach the node i-1 to the node x , you attach the node i to x.( i will be the another children for x )

    → Reply
»
8 years ago, # |
  Vote: I like it +7 Vote: I do not like it

Nice contest. Can you elaborate more the second solution of D ?

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +20 Vote: I do not like it

    Note that for operation 1~3 we will only change one line at a time. So there are at most 10^5 different lines. We can use array/bitset to maintain these lines. Lets call this array/bitset lines[]. We also need to know after each operation, where these lines are stored. So we need a new array position[][]. position[op][i] means after the op-th operation, the status of the i-th line is stored in lines[position[op][i]].

    When we use operation 1~3, we just add a new line to lines[]. And after each operation, we will need to update position[][]. If we use operation 1~3, only position[op][i] will change to the newest added line. If we use operation 4, we just need to iterate through all lines, and let position[op][i] = position[x][i].

    You can also see my submission for details (I use a bitset to maintain lines[]) 20015649

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      goto is not good,you can use continue instead

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      I guess we can just use string here instead of bitset. Bitset has a little more overhead.

      When using string, we could add another field inverted that basically keep track of # times operation 3 applied % 2. inverted == 1 means every bits in the string are inverted, otherwise not.

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Your complexity is O(n*q). This means O(10^8) worst case. How can this fit in 2 seconds?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I'm not quite sure about the speed of the judge server, but the following code can be executed within 1 second on my laptop (just a normal laptop, not a very good one).

        #include <stdio.h>
#include <time.h>
int main()
{
    int i;
    for(i=1;i<=300000000;i++);
    printf("%d",clock());
    return 0;
}

        So I think O(10^8) can be executed within 2 seconds.

        → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I guess if he use memcpy instead of coping by loop it would be faster. Despite the fact that memcpy also loops it's so much faster.

        → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I did as you told, but I've got TL — 20157774

      → Reply
»
8 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

Problem D. also has an online persistant segment tree solution. 19996544

→ Reply
»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Another solution to problem E.

Note that the data is delivered all at once (offline). We can precalculate the sum of the happiness value of each garland in each rectangle given in the "ASK" operation (using two-dimentional Binary Indexed Tree/Fenwick Tree). Then for every "ASK" operation we just need to enumerate all the garland and see if it is on. If the garland is on we can add the precalculated value to the answer.

The time complexity is O(nm(log(2000))^2). You can see my submission for detail 20021444

→ Reply
»
8 years ago, # |
  Vote: I like it +24 Vote: I do not like it

I know this is your first editorial but I think editorials should be more detailed, editorials should be 'editorials' if that makes any sense. Thanks for the round.

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anyone add the solution to the second problem? My code is http://ideone.com/fOzg7O. Please tell me where I am wrong.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    1. Your solution gives WA, because you create arrays u1[m], v1[m], l1[m] of size m. But following cycle can add 2m edges. So this solution works correctly.

    2. Now we have TLE. That is because your solution works at least in O(m*k). You can see 19989181 — my contest submission, which works in O(m + k).

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      How can there be 2m edges?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        In cycles for an edge (u[i], v[i]) if both cities u[i] and v[i] have flour storage, then the edge appended twice.

        → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

There is another solution to C , which gives you all pythagorean triplets in O( 500* sqrt(side ) ) . 20008793

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    1. Would you please explain a little ...

    2. I think order of your solution should be more because there is another loop inside a sqrt(side) loop ... isn't it ?!

    → Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    In O() we don't use a number... it should be a variable or something ... for example max_factors or something. ....

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I know that buddy , its done to make life simpler :)

      → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone please explain the editorial solution of E? I could not understand it properly. What is 'concrete garland' and 'extreme point'? How are we handling 'garland which lies entirely within the request'?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    There are only 2000 ASK queries. For each ask query let us precompute for each garland the sum it will contribute if this garland was on. This can be done by a 2-D BIT. This will take time equal to O(ASKQ * K * logN * logM).

    Then for each switch query just keep an array which will denote whether each garland is currently on or off. For each ask query, iterate over all garlands, if it is on, add to the answer the previously computed sum.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +4 Vote: I do not like it

      I understood this one. But is this the one explained in the editorial? I don't think so. Please correct me if I'm wrong. :)

      → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    Its almost like he doesn't want us to understand what he wrote facepalm

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    The solution in editorial uses prefix sums of values in garland to find answer to a query. Whenever a garland enters the frame, subtract prefix sum from answer, and whenever a garland leaves the frame, add prefix sum to answer. Also, for a garland ending inside the frame, add the prefix sum of its end to the answer. Do all these operations only for "on" garlands.

    There will be O(n+m) such entries and exits, hence time complexity: O(2000 * (n + m))

    → Reply
»
8 years ago, # |
  Vote: I like it +7 Vote: I do not like it

In solution for B I believe that this If there is such a pair of cities, print -1. should be rewritten to ..if there is NO such pair..

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Someone please explain the editorial of E

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 3   Vote: I like it +9 Vote: I do not like it

    In problem E. there are at max 2000 ASK queries. And k<=2000. So for each ASK query basically we are calculating our answer separately for each garland. Now we arrive at two cases :

    1. When the entire garland is in our rectangle (the one in query) This can be checked in O(1) for all the garlands by storing the extreme points . That is storing the topmost, leftmost,rightmost, bottommost. If all these points are inside the boundary, then we simply add the sum of all the values in garland to our answer.

    2. If some part of the garland is inside and rest is out, then at least one of its lighthouse must be present on the boundary. While taking the input, for each garland we can number all the lightbulbs in the order of input (Consecutive in the grid), and we can make an array of pair of integers where for each cell we store the garland number and the index of the lighthouse. Now we need to iterate through the four boundaries and we need to store the indeces where some garland exits or enters the rectangle. This can be easily done. Refer to my implementation. Now with this information we need to calculate the sum of lightbulbs in the rectangle, which can be done by storing the prefix sums for each garland.

    Time Complexity : O (q* (n+m+klogk)) where q<=2000 Here is my implementation : 20021555

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Got it!

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      You are also sorting the positions for each garland.That would bring another logn.

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Yes it will. Totally forgot about it.Thanks

        → Reply
    • »
      »
      »
      3 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Since the maximum length of a garland is $$$2000$$$, we can use counting sort instead of ordinary sort and bring the complexity to $$$O(ASK * (n + m + k))$$$.

      Also, when checking for garlands that lie completely inside, we don't need to check extreme points (minX, maxX, ...) as the editorial said. Instead, we can take any point of the garland and check if it lies inside the rectangle. Since we have checked all border cells, if any point of the garland lies inside the rectangle, then it has to lie totally inside. We can conveniently check the last point, since we need to check it anyways.

      This is my implementation 126593034. Sadly, in this problem, solutions with $$$log$$$ are indistinguishable from linear ones, and even $$$log^2$$$ ones can pass.

      → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What's the time complexity of problem E.

→ Reply
»
8 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Can you explain about problem D using dfs

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    Let's construct graph, where every vertex is state of our bookcase. Initialy we have one vertex corresponding to the initial state of bookcase. Let's process all queries. We will create new vertex every time we find queries of type 1, 2, 3. Also we make new edge from current vertex to the new one. On queries of type 4 we just change our current state(without changing the graph). Then we travel across graph with dfs and apply every change of bookcase written on the edge.

    Sorry for my english. Here is the code. I hope it will help.

    → Reply
»
8 years ago, # |
  Vote: I like it +15 Vote: I do not like it

Worst editorial ever !!

→ Reply
»
8 years ago, # |
  Vote: I like it +7 Vote: I do not like it

Why there isn't any editorial for C ?!

→ Reply
»
8 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

Thanks for the great round.

Would like to know if anyone could do O(q) or anything better than O(qm) online solution of problem D?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Yes there is an online O(qlogn) solution using persistant segment tree. 19996544

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thanks for the tips!

      I found a pretty good explanation of persistent segment tree here for anyone might be interested. If you know this the solution could be super straightforward.

      Note that it's actually a simplified persistency, compare to real persistency like partial persistency and full persistency. There is a pretty good youtube video course that would walk you guys through those ideas if you are interested, see here.

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      how did you handle range updates?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Lazy propogation.

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          yeah i tried lazy propagation but i am stuck in a point.Point updates are clear like

          Point updates for a particular query means that we have to change only log(n) nodes in path from root to leaf so for q queries space complexity would be n+qlog(n) but for the case of range updates i would keep a lazy value at each node but the problem i am facing is that the node to be updated would be representing some range so to change it would mean recreating the whole structure beneath it which be be too much costly considering the fact that there might be more range updates in the queries.Can someone suggest how to implement this?

          I implement lazy propagation like this in normal segment tree first when i need to update a range i update the node representing the node and if it is not a leaf node i pass the lazy update to its two children but here if i just create a new node and pass the lazy value down this will contradict with some other k used before.

          → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In Problem E, there is another offline solution which uses persistent segment tree. Note that 2d range query can be done in O(log n) with a persistent segment tree. So for each garlands, add its lightbulbs' weights to their coordinates to the persistent segment tree. Now for each ASK queries, we can determine how much the garland will affect to the answer by summing the rectangle area. After calculating them, we follow the queries again, turn on/off garlands, and calculate the answer. Time complexity is O(q+k(len log len + len log 2000 + s log 2000)+ks). (s is the number of ASK queries)

http://mirror.codeforces.com/contest/707/submission/20108841

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can you help me regarding range updates in persistent segment tree referring to my above comment?

    → Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I'm having difficulties with question B — Bakery. Can someone help me with what i'm doing wrong

https://mirror.codeforces.com/contest/707/submission/78816637

→ Reply