Спасибо всем, кто написал раунд. Надеюсь, задачки вам понравились.
A — Фотографии Брейна
Нужно сделать ровно то, что написано в задачке: считать все символы, и, если есть хоть один из набора {C, M, Y} вывести "#Color" иначе — "#Black&White"
B — Пекарня
Заметим, что нет смысла выбирать город для пекарни и город со складом так, чтобы между ними было больше одной дороги, т.к. каждая дорога увеличивает расстояние, за которое нужно платить.
Таким образом, задача сводится к следующей: выбрать два соседних города так, чтобы в одном был склад, а в другом — нет. Для этого просто перебираем все города со складом, среди соседей каждого ищем город без склада и обновляем ответ. Если такой пары городов нет, выводим -1.
C — Пифагоровы тройки
Пожалуй, самая интересная задачка этого раунда.
Формализуем задачку:
Дано число a. Найти такие два числа b и c, чтобы выполнялось одно из следующих двух равенств:
a2 = b2 + c2 или a2 = abs(b2 - c2)
Давайте разберемся, когда ответ найти невозможно.
Если а = 1. Доказательство:
1 = b2 + c2 — невозможно
1 = abs(b2 - c2) — невозможно, т. к. не существует таких двух квадратов чисел, что разница между ними равна 1.
Если a = 2. Доказательство:
4 = b2 + c2 — невозможно.
4 = abs(b2 - c2) — невозможно, т. к. минимальная разность квадратов двух чисел, больших единицы равна 5.
Теперь решение для остальных чисел:
Если а — нечетное:
b = a2 / 2, c = a2 / 2 + 1, где " / " — целочисленное деление.
Тогда c2 - b2 = (c - b) * (c + b) = (1) * (a2) = a2.
Если a — четное:
Поделим а на 2. Тогда получится либо нечетное число, в таком случае, решаем задачку для (a / 2), а потом домножаем b и c на два:
b = (a2 / 4) * 2, c = (a2 / 4 + 1) * 2, где " / " — целочисленное деление.
Либо получится опять четное число. В этом случае исходное число а кратно четырем. И для решения используем известную Пифагорову тройку {3, 4, 5}:
b = 3 * (a / 4)
c = 5 * (a / 4)
D — Персистентный шкаф
Решение №1:
Заметим, что данные подаются все и сразу(offline). Тогда мы можем построить дерево версий, потом запустить DFS из корня и честно обрабатывать каждый запрос при переходе из вершины в вершину.
Решение №2:
Заметим, что Алина не использует операции, которые относятся к столбцам. Мы можем завести массив версий полок, а каждую версию шкафа представлять в виде массива индексов соответствующих полок и явно её хранить. Тогда при операции, как-то изменяющей шкаф, создается новая версия полки, которая была изменена, индекс этой версии записывается на позицию прежней полки. Этот подход избавляет решение от использование лишней памяти для хранения ненужной информации.
E — Гирлянды
Давайте обрабатывать каждый запрос следующим образом:
Пройдем по "рамке" запроса и запомним лампы гирлянд, которые лежит на границе. Тогда, чтобы для конкретной гирлянды найти, какая её часть лежит внутри запроса, просуммируем все её отрезки, концами которых являются лампы, лежащие на "рамке".
Также нужно не забыть те гирлянды, которые лежат полностью внутри запроса. Для каждой гирлянды в самом начале найдем крайние точки, и, чтобы проверить, лежит ли она полностью внутри запроса, проверим, лежат ли внутри него её крайние точки.










Кто может чуть более подробно разъяснить 2е решение задачи D. Как-то не понятно как должны изменяться со временем хранимые в памяти данные.
При каждой операции изменения изменяется не более одной полки. Тогда можно ту полку, что изменяется, добавлять по новой в вектор полок, обновляя нужные позиции в ней. Можно иметь какой-нибудь вектор массивов булов для хранения этого дела. Также поддерживаем вектор массивов
шортовинтов для хранения списка полок (их индексов) шкафа после k-той операции. При операции 4 типа просто берем шкаф из k-той операции и пушим его в текущую.По памяти в итоге 10^5 * 10^3 для полок и 10^5 * 10^3 * 4 для шкафов. Что-то около 490 мб должно выходить, кажется.
Второе решение задачи D в итоге оффлайновое или онлайновое? Существует ли онлайновое решение?
Онлайновое.
Есть еще онлайновое для n <= 105, но я такое писать не умею :D
А как 4 операцию делать?
Для 1/2/3 операций я копирую и изменяю битсет полки. Для каждой полки есть вектор с парами времен эвента и ссылкой на номер последнего битсета.
При 4 запросе я для каждой полки ищу lower_bound-ом по k номер соответствующей версии полки и добавляю пару с текущим временем и найденной версии в каждую полку — дает TL 28.
А зачем там lower_bound? Можно для каждой версии шкафа итеративно присваивать номер, тогда так и обращаться в k-тый экземпляр.
У меня на абсолютно каждую версию хранится вектор индексов полок, входящих в данный шкаф, и отдельно еще массив с суммой единиц на полке (да, я не умею в битсеты)
http://mirror.codeforces.com/contest/707/submission/20009104
Сделал почти также. Превысил ограничение по памяти. 20012349
Да, там надо довольно аккуратно писать. И если в векторе со шкафами меньше интов взять ничего не получится, то в полках достаточно векторов чаров/булов или битсетов, там ведь только нули и единицы хранятся. Так в худшем случае должно быть около 490 мб.
Точняк. Совсем забыл, что полки в bool надо сделать. Всё прошло. 20012931
Есть онлайн решение, реализовал персистентное дерево отрезков по строкам. А саму строку храню в bitset, это хорошо работает т.к. bitset можно ксоритьБ а также есть полезная для данной задачи функция count(). Оценка сложности q*log(n)*m/32. Решение
Сделал, как описано. Получаю TL на тесте 70 либо ML на тесте 47. Для поддержания полок пробовал разные структуры:
vector <bool>— 20155806vector <char>— 20150187bitset— 20150105 — код с комментариями UPD:20157774struct state{ bool val[MAXN]; }— 20154885Кто может объяснить, может ли путь до пекарни пролегать через другие города в задаче B? А если нет, как трактовать условие "между городами b и s существует путь по дорогам суммарной длины x (если путей несколько, Маша вправе выбирать, какой именно путь будет использован)."?
Может, конечно, но лучший вариант всегда будет напрямую от склада до пекарни, то есть по одной дороге не проходя через другие города
Можно объяснить разбор задачи D и Е поподробней? А то прочитал и появилось чувство, что тупой)) Можно авторский код?
Действительно, неплохо бы было привести ссылки на авторские решения. Тоже ничего не понял из разбора последних 2 задач :(
Хочу поблагодарить автора за интересные задачи, но такое ощущение, что разбор писался с где-нибудь в переполненном автобусе на какой-нибудь старенькой nokia.
Так не годится, если уж делать разбор, то делать круто, а то больше похоже на то, посмотрите какой я крутой.
У меня одного написано "Разбор недоступен"?
Не, тоже только что хотел написать
Либо я чего-то не понял, либо я совсем по-другому решил задачу Д. Как минимум в обоих решениях я вижу надпись "дерево версий", в то время как у меня хранится лишь одна версия шкафа всегда. Как я этого добился? Я построил граф на запросах и обошел его ДФСом (вот этот момент совпадает с первым решением). В графе в вершине хранится следующая операция для выполнения, но в одной вершине i так же будут хранится все операции вида "4 i". Тогда при обработке одной операции я вычисляю для неё ответ, вызываю ДФС из следующей операции, а по возвращении из ДФСа откатываю изменения (благо операции позволяют это сделать). Таким образом, операции выполняются не в хронологическом порядке, и каждая операция выполняется два раза (прямая и обратная), но всё это позволяет храниться лишь одну версию шкафа. Так же, для того чтобы не мучится с деревом отрезков и проталкиванием операции "переворота полки", я храню одну полку в len = 20 числах типа long long (по 50 бит в одном числе), что позволяет мне за О(1) делать операции поставить/убрать книгу и за O(len) — "перевернуть полку". Итого: O(q * len) времени и O(n * len + q) памяти.
Код решения
Этот граф и имеется ввиду под определением "дерево версий"
Для меня это немного не интуитивное определение, учитывая, что сами версии мы не храним, а лишь несколько раз в них попадаем, выполняя операции. Но, скорее всего, я просто первый раз столкнулся с таким определением.
На самом деле переворачивать можно за O(1), так как нам нужно только количество книг на полке, а не их координаты. Итоговая асимптотика будет O(q).
Количество книг можно узнать за О(1) — да, но что делать, если после этого нужно поставить/убрать книгу, а у нас уже нет валидной полки с расстановкой книг? Хотя тогда можно заморочиться и считать количество переворотов, вычислять стоит сейчас книга всё-таки или нет и ставить/убирать, если надо.
У нас есть перестановка, но она либо прямая, либо инвертированная. Значит нужно дополнительно хранить для каждой полки ее состояние. Пример для запроса первого типа: 1) если полка прямая и место не занято, то увеличиваем ответ, иначе ничего не меняем, 2) если полка инвертированная и место занято (так как состояние самой полки мы не меняем, а только флаг), то увеличиваем ответ, иначе нечего не делаем.
Теперь, как пересчитывать ответ, когда идет переворот, для этого дополнительно будем хранить количество занятых мест на полке. И тогда когда переворачиваем полку, ответ меняется так: ans = ans - b[xi] + (m - b[xi]), b[xi] = m - b[xi].
Моё решение: 19996879.
На самом деле я у себя пересчет ответа делал именно так изначально (у меня даже массив сумм так же называется — b). А переворот полки я совершал только чтобы потом легче можно было выполнять операции 1 и 2 типа.
В принципе, такой подход достаточно популярен, когда нам не нужны сами состояния, а только какая-та функция на ними.
Поясните, пожалуйста, решение задачи D (решение №1), а то не понятно :(
Выше мой большой комментарий описывает подробно это решение.
Ещё в задаче D можно было не долго думать, а написать персистентное дерево отрезков, упорядочив шкаф как линейный массив.. =)
А в задаче Е — считать все запросы, потом для каждой пары "гирлянда — ASK-запрос" посчитать с помощью дерева Фенвика сумму лампочек на прямоугольнике запроса, а потом, отвечая на запросы, только добавлять или нет значение предпосчитанной суммы в зависимости от того, включена гирлянда или нет.
Можно было еще для каждой гирлянды при помощи сканлайна сделать тоже самое, только сразу для всех прямоугольников, будет асимптотически быстрее.
персистентное дерево отрезков с проталкиванием
Объясните Сшку, пожалуйста
Разница между квадратами двух соседних чисел всегда есть нечетное число. Например,
4 - 1 = 3,9 - 4 = 5и т.д. Можно также заметить, что все разницы образуют арифметическую прогрессию. Благодаря этому, можно достаточно легко от разницы прийти к самим числам и обратно. Если разница равна нечетномуA^2, то первое число будетA^2/2, а второе число на единицу больше первого. Например,A = 9,B = A^2/2 = 40,C = 41. Если жеA— четное, тогда и разницаA^2— четная, то можно поделитьАна максимальную степень двойки, найти ответ таким же образом и домножить его на эту степень. Исключением являются разницы дляA = 1иA = 2, для них найти ответ нельзя. А так же стоит отметить случай, когдаАуже равна степени двойки (деление на максимальную степень двойки приведёт нас к1, для которой ответ найти не получится), в этом случае, поделивАна степень двойкиX, надо получитьА = 4, а для катета равного четырём существует Пифагорийская тройка(3, 4, 5). В этом случае ответ будет соответственно3 * Xи5 * X. Данное решение немного отличается от описанного в разборе.Код решения
Это решение для катета, а что если ввести длину гипотенузы?
Любой отрезок длиной больше 4-х может быть как катетом, так и, возможно, гипотенузой.
Хммм, довольно интересно, спасибо
Can you please give the tutorial for Problem C — Pythagorean Triples?
n = 1, 2: There are no solutions (easy to prove)
n is even: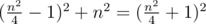
n is odd: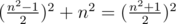
Do you have a proof for the formula ?
You can prove it by induction.. Check the base case by considering the case that sum of two sides of triangle is greater than the third side. This will give you n>1 for odd 'n' and n>2 for even 'n'.
You can directly substitute and check using (a + b)2 = a2 + b2 + 2ab formula.
No need of induction.
For instance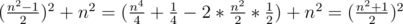
how can i come with such a formula if i didn't know it before ?
Actually you can figure it out easily. You see that n²=m²-k²=(m-k)×(m+k), so you need to find a way to present n² as a×b with (a-b) is even. You will always find a and b if n is odd and larger than 1, which is 1 and n². If n is even and n is larger than 2 then how about 2 and n²/2. Easy as that, huh?
http://mirror.codeforces.com/blog/entry/46681 explains it.
The second formula for odd numbers is easier to see in the following form —
(k)^2 + (2k + 1) = (k + 1)^2
If n is odd, it's square is also odd ... so** n^2 = 2k + 1**, and the equation is re-written in terms of n.
If n is even ... i.e.** n = 2m**, then** n^2** is also even ... so n^2 = 4k .. a multiple of 4. Using that observation,
then
(k — 1)^2 + (4k) = (k + 1)^2
Again the equation is re-written in terms of** n**.
consider a^2 = b^2 + c^2 (PT)
now we are given the cathetus (any of the two sides other than hypotenuse) let c = n then -> n^2 = (a-b)*(a*b) [a^2 — b^2]
check yourself that either (a-b) and (a+b) both are even else both are odd
from the above eqn (a-b) and (a+b) are factors of n^2
simplest -> if n is odd let (a-b)=1 and (a+b)=n^2
if n is even let (a-b)=2 and (a+b)=n^2/2
solve these and u will get values for a and b :) but for n<=2 no ans exists so print -1 :)
Brilliant explanation .
why did you assume that if n is odd you put a-b =1 why 1 not any odd number .and the same if n is even ?
I said that's the simplest.... Plus u need a-b to be a factor of n^2 and 1 is a factor of every number that's why a-b=1 same goes if n^2 is even
Your_dad, actually we are given either cathetus or hypotenuse. Is there always exist a Pythagorean triple in which given n represent cathetus? How can we prove that?
Let n = 2k where k > 1. Consider the Pythagorean triple obtained by scaling (3, 4, 5) by .
.
Now suppose n has some odd prime factor. Every odd prime p is the difference of two consecutive squares. Let x be such that (x + 1)2 - x2 = 2x + 1 = p. Thus, (p, 2x(x + 1), x2 + (x + 1)2) is a Pythagorean triple. Scale it by and you obtain a triple that has n as a cathetus.
and you obtain a triple that has n as a cathetus.
Thus, every integer n > 2 is a cathetus of at least one right triangle.
How to prove that for n <= 10^9 and n is a cathetus, there exists c <= 10^18 where n^2 + x^2 = c^2?
For the case of 2k, it's trivial, so suppose n has an odd prime factor p = 2x + 1 as in my previous comment. We can show that my scaled right triangle will be small enough for the problem:
As for the hypotenuse:
Note that in the last step, the reason $x+2 \leq p$ is because x ≥ 1 since p is at least 3.
[http://www.codeforces.com/blog/entry/46681] try this:P
Hi
You could refer this explanation. :D
Problem D solution no.1
Does that mean if there's op is '4', then the tree contains a cycle?
No. in the case of 4 x , you don't attach the node i-1 to the node x , you attach the node i to x.( i will be the another children for x )
That's awesome
Nice contest. Can you elaborate more the second solution of D ?
Note that for operation 1~3 we will only change one line at a time. So there are at most 10^5 different lines. We can use array/bitset to maintain these lines. Lets call this array/bitset
lines[]. We also need to know after each operation, where these lines are stored. So we need a new arrayposition[][].position[op][i]means after the op-th operation, the status of the i-th line is stored inlines[position[op][i]].When we use operation 1~3, we just add a new line to
lines[]. And after each operation, we will need to updateposition[][]. If we use operation 1~3, onlyposition[op][i]will change to the newest added line. If we use operation 4, we just need to iterate through all lines, and letposition[op][i] = position[x][i].You can also see my submission for details (I use a bitset to maintain
lines[]) 20015649goto is not good,you can use continue instead
I guess we can just use string here instead of bitset. Bitset has a little more overhead.
When using string, we could add another field inverted that basically keep track of # times operation 3 applied % 2. inverted == 1 means every bits in the string are inverted, otherwise not.
Your complexity is O(n*q). This means O(10^8) worst case. How can this fit in 2 seconds?
I'm not quite sure about the speed of the judge server, but the following code can be executed within 1 second on my laptop (just a normal laptop, not a very good one).
So I think O(10^8) can be executed within 2 seconds.
I guess if he use
memcpyinstead of coping by loop it would be faster. Despite the fact that memcpy also loops it's so much faster.I did as you told, but I've got TL — 20157774
Problem D. also has an online persistant segment tree solution. 19996544
why do you do this lz = lz^lazy; in update1 . ?
Another solution to problem E.
Note that the data is delivered all at once (offline). We can precalculate the sum of the happiness value of each garland in each rectangle given in the "ASK" operation (using two-dimentional Binary Indexed Tree/Fenwick Tree). Then for every "ASK" operation we just need to enumerate all the garland and see if it is on. If the garland is on we can add the precalculated value to the answer.
The time complexity is O(nm(log(2000))^2). You can see my submission for detail 20021444
Моё решение по Е: построим дерево Фенвика для каждой гирлянды по отдельности. Переключение гирлянды будем выполнять за O(1), а поиск ответа за O(qask * k * log n log m). Теперь встаёт вопрос лишь о том, сколько памяти будет занимать одно дерево Фенвика. Разумеется, если на него выделить O(n*m) памяти, то суммарный объём памяти превысит 1 гигабайт в несколько раз. Поэтому можно сжать область для построения дерева до габаритных размеров гирлянды. Допустим, все гирлянды представляют из себя прямые линии, то тогда на одну гирлянду будет уходить O(len) памяти, что приемлемо. Если же представить гирлянду в виде квадрата, то потребуется тот же объём памяти O(sqrt(len)*sqrt(len)), что так же приемлемо. Но если представить гирлянду в виде "змейки" (одна клетка вправо, одна вверх и т.д.), то потребуется O(len/2 * len/2) памяти, что уже очень много. Но встаёт вопрос о том, сколько максимально может быть таких "змеистых" гирлянд. Расположим такие гирлянды следующим образом: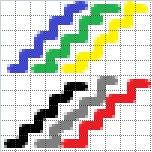
Очевидно, что таких гирлянд может быть по крайней мере половина из всех возможных. То есть объём занимаемой памяти составит O(len/2 * len/2 * k/2), а учитывая, что требуется хранить числа типа long long, это будет около 8 гигабайт.
Перед тем, как писать это решение я сразу подумал о том, как его оптимизировать. Так как для змеистых гирлянд очень много элементов дерева Фенвика будут равны нулю, то можно построить это дерево на структуре map, благодаря чему мы не выделим лишней памяти. Но тогда во время работы добавится третий логарифм. Второй способ оптимизировать — построить дерево отрезков, только не в простой форме, а в виде структуры данных, в которой хранятся ссылки на левого и правого сына. Если в какой-то вершине сумма равна нулю, то нам не нужно спускаться ниже по дереву отрезков, и, более того, не требуется хранить дальнейшее разбиение.
Решения с описанными оптимизациями я написать не успел потому, что моё первоначальное решение, на моё удивление, зашло, потребив всего 36 мегабайт памяти. Теперь вопрос к автору задач: есть ли тесты с подобными "змеевидными" гирляндами?
Код решения
Чтобы сэкономить память можно было делать задачу в оффлайне. После построения дерева Фенвика для i-ой гирлянды мы сразу выполняем все запросы, которые нам потом понадобятся. После этого текущее дерево нам уже не нужно и мы удаляем его, таким образом в памяти хранится только одно дерево.
Спасибо. Но я уже два раза читал про этот вариант решения. И суть моего сообщения — поведать о том, какой монстр случайно зашел, хотя должен был не пролезть в ограничения.
I know this is your first editorial but I think editorials should be more detailed, editorials should be 'editorials' if that makes any sense. Thanks for the round.
Can anyone add the solution to the second problem? My code is http://ideone.com/fOzg7O. Please tell me where I am wrong.
Your solution gives WA, because you create arrays
u1[m], v1[m], l1[m]of sizem. But following cycle can add2medges. So this solution works correctly.Now we have TLE. That is because your solution works at least in O(m*k). You can see 19989181 — my contest submission, which works in O(m + k).
How can there be 2m edges?
In cycles for an edge
(u[i], v[i])if both citiesu[i]andv[i]have flour storage, then the edge appended twice.There is another solution to C , which gives you all pythagorean triplets in O( 500* sqrt(side ) ) . 20008793
Would you please explain a little ...
I think order of your solution should be more because there is another loop inside a sqrt(side) loop ... isn't it ?!
Well , you are quite correct , I tried to approximate the number of factors of a 9 digit number and https://en.wikipedia.org/wiki/Highly_composite_number and in rare cases number of factors go beyond 500 but since it was sqrt( 10^9 ) * 500 so it worked.
In O() we don't use a number... it should be a variable or something ... for example max_factors or something. ....
I know that buddy , its done to make life simpler :)
Can someone please explain the editorial solution of E? I could not understand it properly. What is 'concrete garland' and 'extreme point'? How are we handling 'garland which lies entirely within the request'?
There are only 2000 ASK queries. For each ask query let us precompute for each garland the sum it will contribute if this garland was on. This can be done by a 2-D BIT. This will take time equal to O(ASKQ * K * logN * logM).
Then for each switch query just keep an array which will denote whether each garland is currently on or off. For each ask query, iterate over all garlands, if it is on, add to the answer the previously computed sum.
I understood this one. But is this the one explained in the editorial? I don't think so. Please correct me if I'm wrong. :)
Its almost like he doesn't want us to understand what he wrote facepalm
The solution in editorial uses prefix sums of values in garland to find answer to a query. Whenever a garland enters the frame, subtract prefix sum from answer, and whenever a garland leaves the frame, add prefix sum to answer. Also, for a garland ending inside the frame, add the prefix sum of its end to the answer. Do all these operations only for "on" garlands.
There will be O(n+m) such entries and exits, hence time complexity: O(2000 * (n + m))
In solution for B I believe that this
If there is such a pair of cities, print -1.should be rewritten to..if there is NO such pair..Someone please explain the editorial of E
In problem E. there are at max 2000 ASK queries. And k<=2000. So for each ASK query basically we are calculating our answer separately for each garland. Now we arrive at two cases :
When the entire garland is in our rectangle (the one in query) This can be checked in O(1) for all the garlands by storing the extreme points . That is storing the topmost, leftmost,rightmost, bottommost. If all these points are inside the boundary, then we simply add the sum of all the values in garland to our answer.
If some part of the garland is inside and rest is out, then at least one of its lighthouse must be present on the boundary. While taking the input, for each garland we can number all the lightbulbs in the order of input (Consecutive in the grid), and we can make an array of pair of integers where for each cell we store the garland number and the index of the lighthouse. Now we need to iterate through the four boundaries and we need to store the indeces where some garland exits or enters the rectangle. This can be easily done. Refer to my implementation. Now with this information we need to calculate the sum of lightbulbs in the rectangle, which can be done by storing the prefix sums for each garland.
Time Complexity : O (q* (n+m+klogk)) where q<=2000 Here is my implementation : 20021555
Got it!
You are also sorting the positions for each garland.That would bring another logn.
Yes it will. Totally forgot about it.Thanks
Since the maximum length of a garland is $$$2000$$$, we can use counting sort instead of ordinary sort and bring the complexity to $$$O(ASK * (n + m + k))$$$.
Also, when checking for garlands that lie completely inside, we don't need to check extreme points (minX, maxX, ...) as the editorial said. Instead, we can take any point of the garland and check if it lies inside the rectangle. Since we have checked all border cells, if any point of the garland lies inside the rectangle, then it has to lie totally inside. We can conveniently check the last point, since we need to check it anyways.
This is my implementation 126593034. Sadly, in this problem, solutions with $$$log$$$ are indistinguishable from linear ones, and even $$$log^2$$$ ones can pass.
What's the time complexity of problem E.
Can you explain about problem D using dfs
Let's construct graph, where every vertex is state of our bookcase. Initialy we have one vertex corresponding to the initial state of bookcase. Let's process all queries. We will create new vertex every time we find queries of type 1, 2, 3. Also we make new edge from current vertex to the new one. On queries of type 4 we just change our current state(without changing the graph). Then we travel across graph with dfs and apply every change of bookcase written on the edge.
Sorry for my english. Here is the code. I hope it will help.
Worst editorial ever !!
Why there isn't any editorial for C ?!
There is a nice page explaining it, see here.
Thanks for the great round.
Would like to know if anyone could do O(q) or anything better than O(qm) online solution of problem D?
Yes there is an online O(qlogn) solution using persistant segment tree. 19996544
Thanks for the tips!
I found a pretty good explanation of persistent segment tree here for anyone might be interested. If you know this the solution could be super straightforward.
Note that it's actually a simplified persistency, compare to real persistency like partial persistency and full persistency. There is a pretty good youtube video course that would walk you guys through those ideas if you are interested, see here.
how did you handle range updates?
Lazy propogation.
yeah i tried lazy propagation but i am stuck in a point.Point updates are clear like
Point updates for a particular query means that we have to change only log(n) nodes in path from root to leaf so for q queries space complexity would be n+qlog(n) but for the case of range updates i would keep a lazy value at each node but the problem i am facing is that the node to be updated would be representing some range so to change it would mean recreating the whole structure beneath it which be be too much costly considering the fact that there might be more range updates in the queries.Can someone suggest how to implement this?
I implement lazy propagation like this in normal segment tree first when i need to update a range i update the node representing the node and if it is not a leaf node i pass the lazy update to its two children but here if i just create a new node and pass the lazy value down this will contradict with some other k used before.
In Problem E, there is another offline solution which uses persistent segment tree. Note that 2d range query can be done in O(log n) with a persistent segment tree. So for each garlands, add its lightbulbs' weights to their coordinates to the persistent segment tree. Now for each ASK queries, we can determine how much the garland will affect to the answer by summing the rectangle area. After calculating them, we follow the queries again, turn on/off garlands, and calculate the answer. Time complexity is O(q+k(len log len + len log 2000 + s log 2000)+ks). (s is the number of ASK queries)
http://mirror.codeforces.com/contest/707/submission/20108841
Can you help me regarding range updates in persistent segment tree referring to my above comment?
Написал все возможные решения по Е и вот что получилось:
Моё первоначальное решение с деревом Фенвика, которое в теории вообще не должно работать — 1.3 с и 36 мб.
Первоначальное решение оптимизированное структурой map — Time Limit.
Первоначальное решение оптимизированное деревом отрезков без хранения границ — 1.6 с и 150 мб.
Первоначальное решение оптимизированное деревом отрезков с хранением границ — 1.7 с и 190 мб (странно, что работает дольше...).
Решение с преподсчетом ответов на все запросы для каждой гирлянды через дерево Фенвика — 1.9 с и 110 мб.
Решение из разбора (наговнокодил немного) — 2.2 с и 95 мб.
Вывод: надо писать то, что в теории не работает, и быть может оно отработает быстрее и потребует меньше памяти, чем прочие решения.
Тыкнул по первому попавшемуся (полному) решению 20009296. И сразу возник вопрос: как вообще так?
1е6 запросов * 2000 лампочек * (еще какая-то сложность, логарифм, вероятно) = PROFIT
А авторское решение не заходит..
I write a solution for problem C in my blog. If you can't solve this problem, check out this link!
I'm having difficulties with question B — Bakery. Can someone help me with what i'm doing wrong
https://mirror.codeforces.com/contest/707/submission/78816637
-->u did'nt took the visited array to mark the storage locations coz they woud'nt be the part of your ans ! u can refer this (https://mirror.codeforces.com/contest/707/submission/79922973)
Чутка поздновато но я хотел бы попонятнее обьяснить задачу С.
Если выписать все квадраты получим последовательность 1, 4, 9, 16, 25, 36, 49....
Разность между соседними элементами 3, 5, 7, 9, 11, 13, 15, 17...
Для нечетных:
Таким образов всегда существует решение для нечетных n, так как n * n тоже нечетно и мы можем найти эту разность следующим образом: так как каждый раз разница между элементами возрастает на 2 то мы можем найти первое число возведя n в квадрат и поделив на 2 следовательно второе число n * n / 2 + 1.
Для четных:
Посмотрим на разность между двух элементов которые находятся на расстоянии 2 друг от друга:
получим: 8, 12, 16, 20, 24, 28, 32, 36...
Следовательно для любого четного можем найти разность квадратов.
Как найти эту позиции в нашей последовательности? каждое четное число это сумма двух нечетных 8 — 3 + 5, 12 — 5 + 7 и так далее а как найти например 3 мы уже знаем. Итого ответ n * n / 4 — 1 и n * n / 4 + 1