Для начала я хотел бы поблагодарить всех кто принимал участие в создании данного контеста — и его онсайта и заеркала. Также большое спасибо GlebsHP за неоценимую помощь в проведении зеркала.
В прошлом году было целых 4 команды которые сдали все задачи досрочно до конца контеста, поэтому в этом году мы попытались сделать его немного сложнее, Надеюсь что мы не перестарались. Хотелось бы также упомянуть что 2042 команды зарегистрировалось на этот контест, 676 решили хотя бы одну задачу и всего одна команда успела решить все задачи досрочно.
Поздравления, tourist и VArtem с победой в этом соревновании.
Итак, вот список из топ 10 команд по версии заркала BubbleCup на Codeforces:
| 1 | 1322: tourist, VArtem |
| 2 | Um_nik |
| 3 | anta |
| 4 | m3m3t3m3: JoeyWheeler, gongy, rnsiehemt |
| 5 | NanA: jiaqiyang, ExfJoe, AcrossTheSky |
| 6 | Moscow IPT Jinotega: Arterm, ifsmirnov, zemen |
| 7 | HellKitsune |
| 8 | MLW: sokian, Merkurev |
| 9 | uwigmanuke: uwi, snuke, sigma425 |
| 10 | BSUIR POWER: andrew.volchek, netman, teleport |
Все они получат свои футболки. Кроме того, как мы и обещали, 10 футболок мы раздадим случайно выбранным командам из топ 100:
- 95 Singapore zhsh
- 26 Japan natsugiri
- 19 Russia Cryptozool0.6y: Golovanov399, Kostroma
- 12 Rekine: kpw29, Reyna
- 65 China Will not Easily Go Die: wyxoi, Arturia, FHW_SO_WALL
- 82 AkaneSasu
Спасибо всем, Разбор будет опубликован через нескольок часов
Прошу прощения за долгий сбор разбора задач: авторы раскиданы по всему миру — потребовалось несколько дней а не часов. Разбор геометрии будет добавлен как только я получу его от автора, остальные задачи здесь
Автокомментарий: текст был обновлен пользователем ibra (предыдущая версия, новая версия, сравнить).
You said there will be 10 T-shirts for random competitors, not teams!
I also said that whole teams will be getting T-shirts. It would be strange if in a team one gets T-shirt and others dont
I agree, but choosing the teams in this way is not fair, as the probability of getting a t-shirt when you're in a team of 1 is different than if you're in a team of 2 or 3.
Can you please share standings of the onsite contest?
That is all I have now
Мне кажется или вероятность команде из 3 человек получить футболку не такая же, как команде из 1 человека. Поправьте меня если я ошибаюсь, но из-за ограничения в 10 футболок, а не десять команд, рандом сильно искажается.
Editorials ?
In "few hours".
there should be some range of "few hours".
In "few years".
in few decades
in few centuries.
editorial is loading...loading...loading
Editorials ?
we will upload that in "few centuries"
few "forevers"*
How to solve B ?
Deleted
Автокомментарий: текст был обновлен пользователем ibra (предыдущая версия, новая версия, сравнить).
Looks like on test
time and O(n) memory.
100000000 1 100000000
solution for problem B from editorial will work in
Can you please explain your solution of square root complexity?
The main idea is the same as in editorial. How many vertices with cost x·c0 + y·c1 (I mean vertices with x zeroes and y ones)? It is Cxx + y. Now I want to find the (n - 1)-th vertex in non-decreasing order of cost. I will binary search that cost and check if there is enough vertices with this cost or smaller. Now I want to calculate the number of vertices with cost no more than W. For fixed y: x have to be smaller or equal to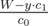
. If y = 0 than all the Cxx + y = 1 and we can calculate its sum in O(1). For all other y we will try all the x and maintain Cxx + y.
time? Because for fixed y we will try no more than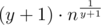 
variants of x or the sum will become greater than n.
Why will it work in
After finding maximal cost I have to calculate the answer. It can be done in a similar way, please refer to my code.
You are right.
We apologize for this. Indeed our solution works in O(NlogN) time and O(N) memory at your test. None of us notices that, we are sorry. Edge test cases contained tests like 10^8 0 10^8, but did not have tests 10^8 1 10^8, our solution works well on tests when 100 <= cost <= 10^8 (and only this kind tests we had). I guess complexity is something like O((maxCost/minCost + logN)*logN), though can't be sure anymore.
If you don't mind I will mark our solution as wrong in editorial and add your square root complexity. Again we are sorry.
Actually there was an idea for a different solution, one with complexity O(log^2(n) log(n c0) ).
Let's assume that c0<=c1. The tree construction from editorial can be viewed in a different way: We have an infinite binary tree with some cost assigned to the nodes. We assign c0+c1 to the root. The cost for the left child is cost of parent + c0 and cost for the right child is cost of parent + c1. We want to select the subset with minimum total cost, since total cost equals to the problem's answer. For the sake of simplicity, before we proceed let's add (c0+c1)*(n-1) to the answer and subtract c0+c1 from every cost.
Let's do binary search on the biggest cost, that we are going to use. To do so, we will need to be able to count the number of nodes with cost, less or equal to C. To count them we use the fact, that it is never necessary to used more than log2(n) expensive letters. So we may iterate on the number of them and sum up the count. If we denote j as the number of expensive letters, then we will be able to use up to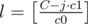
of the cheap ones. Their total count is 
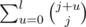. This trivially equals to 
.
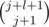Now we know the cost of the most expensive node, we are going to use. How many such nodes are we going to use? n-count(C-1). So now we need to add all nodes, whose cost is less or equal to C-1.
Once again we iterate over the number of expensive nodes j. For taking all the nodes with cost up to C-1 we will have to pay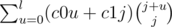
. Probably we may stop at this sum, if we are satisfied with linear solution. To get a fast solution we have to sum it up. After some transformation it may be reduced to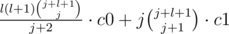 
20620974 implements this solution with complexity O(log^2(n) log(n c0) ).
Awesome solution!By the way,I think this solution is a little bit similar with this:GCJ2014 FINAL D
Can someone tell me how to solve I ?
Problem A in http://www.bubblecup.org/Content/Media/Booklet2016.pdf