Всем привет. Хочу поделиться с общественностью некоторым фактом, который позволяет ломать с гарантией почти любое решение, использующее полиномиальные хэши от строк, где в качестве модуля используется 264 тестом длины порядка нескольких тысяч. Причём, не важно, какое число берётся за точку в полиноме, важно лишь, что все вычисления производятся в типе int64 со стандартными переполнениями — а так пишут большинство олимпиадников.
Для привлечения внимания ключевые слова: не пишите, как написано у е-макса! И только сегодня, только для вас — ломаем решение Petr на задаче 7D - Палиндромность с Codeforces Beta Round #7!
Интересно? Прошу под кат. Для начала, для самых нетерпеливых. Тест генерируется следующим кодом:
const int Q = 11;
const int N = 1 << Q;
char S[N];
for (int i = 0; i < N; i++)
S[i] = 'A' + __builtin_popcount(i) % 2;
// кто не знает, эта функция возвращает
// количество единиц в двоичной записи числа i
Берём и стравливаем на таком тесте решения двух победителей Codeforces Beta Round #7 — Петра Митричева и Влада Епифанова. Решение vepifanov не содержит хэшей и работает правильно — выдаёт ответ 6. Решение же Petr выдаёт ответ 8. Если чуть-чуть подумать, то становится ясно, что ответ на таком тесте к этой задаче есть (Q + 1) / 2 — Влад безусловно прав. Более того, если в качестве Q взять 20, то решение Влада выдаёт правильный ответ 11, а решение Пети — 2055, что совершенно не похоже на правду.
Я утверждаю, что начиная с Q = 11 в этой строке будет очень много различных подстрок, чьи хэши совпадут.
Давайте поймём, в чём дело. Как получается такая строка? Она начинается так:
ABBABAABBAABABBABAABABBAABBABAABBAABABBAABBABAABABBABAABBAABABBA...
Эта строку называют строкой Туэ-Морса по имени товарищей, впервые её упомянувших.
Можно понять, что она получается по рекурсивному правилу S -> S + (not S), стартуя с S = 'A', где под (not S) подразумевается строка после замены A на B и наоборот. Давайте обозначим S для фиксированного Q как SQ.
Вспомним, что есть полиномиальный хэш от строки S длины l. Это есть величина 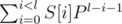 . В качестве P мы берём некоторое нечётное число (не знаю, почему многие считают, что его надо брать простым — это ничем не обосновано).
. В качестве P мы берём некоторое нечётное число (не знаю, почему многие считают, что его надо брать простым — это ничем не обосновано).
Я утверждаю, что hash(S[0... (2k - 1)]) при достаточно малом k совпадёт с hash(S[(2k)... (2k + 1 - 1)]). Иными словами, при Q = 10, hash(SQ) = hash(not SQ). Это будет очень круто, потому что сами по себе SQ и not SQ встретятся в б**о**льших строках много-много раз, что следует из рекуррентного соотношения.
Разберёмся, что значит hash(SQ) = hash(not SQ). Во-первых, можно смело взять вместо ord('A') и ord('B') нули и единицы в коэффициентах многочлена — тем самым мы просто сократим обе части на 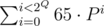 .
.
Что такое hash(not SQ) — hash(SQ)? Нетрудно сообразить, что эта величина есть
--- то есть это знакопеременная сумма степеней P, где знаки чередуются по тому же правилу ABBABAAB... Давайте последовательно выносить из этой суммы множители за скобку:
(возможно, ещё на (-1), но это роли не играет).
А теперь основная фишка — эта величина по модулю 2^64 моментально занулится. Почему?
Давайте поймём, на какую максимальную степень двойки делится каждая из Q - 1 скобок. Заметим, что (i + 1)-ая скобка P2i + 1 - 1 = (P2i - 1)(P2i + 1) делится на i-ую и ещё на какое-то чётное число P2i + 1. Это означает, что если i-ая скобка делится на 2r, то (i + 1)-ая скобка делится по меньшей мере на 2r + 1.
Вот и выходит, что (P1 - 1)(P2 - 1)(P4 - 1)...(P2Q - 1 - 1) делится по меньшей мере на 2·22·23·... = 2Q(Q — 1) / 2. Значит достаточно взять Q >= 12. Ура, анти-хэш построен!
Отсюда и выходит такая маленькая длина теста по сравнению с размером модуля 2^64. Выходит, что размер контртеста есть что-то порядка 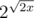 , если используется x-битный тип данных.
, если используется x-битный тип данных.
Мораль: либо не пользуйтесь переполнениями, когда считаете хэши, либо будьте уверены, что в задаче не существует теста, на котором можно подсунуть вашей программе злополучную ABBABAABBAABABBA...
Как такой тест образовался? Первое использование такого теста, которое я знаю, было в 2003 году на городской олимпиаде школьников в Санкт-Петербурге в задаче cubes. Эта задача потом перекочевала в проблемсет ЛКШ, в которой множество школьников старших параллелей много лет натыкалось на WA27, отправляя хэшовые решения. Одним из таких школьников был я — к сожалению, мне никто не смог объяснить. что же это за тест, Burunduk1 поковырялся, поковырялся, но в тесте не разобрался. С тех пор в памяти осталась зарубка о той злосчастной задаче.
И вот, по прошествии пары лет, всё же решил сесть и разобраться, что с ней не так. Спасибо Серёже — он же предложил поделиться с общественностью. Я, к слову, пытался нагуглить хоть какой материал в сети по известным человечеству антихэш-тестам, почти ничего дельного не нашёл. Может это общеизвестное знание, а у меня просто навыков поиска англоязычных статей не хватает?











Вот это круто. Да, тема хаков стала популярна в последнее время.
Придется теперь писать двойные интовые хеши по модулю-не-степени-двойки и тормозить из-за деления.
Двойные интовые необязательно. Да и интовые тоже не очень правильно — нам же приходится домножать на основание, хотелось бы не переполниться — видимо, просто лонг лонговые хэши по какому-нибудь простому модулю порядка 109 видится оптимальным вариантом. Но, опять же, следует помнить про парадокс дней рождения, и как-то стараться соотносить множество значений хэшей с размером множества сравниваемых элементов.
Ну да, я и имел в виду по простому модулю порядка 109. Причем двойные чуть ли не обязательно, т.к. одиночный хеш по столь маленькому модулю валится простым перебором случайных строк менее чем за секунду (тот самый парадокс дней рождения).
P.S. I_love_natalia убедил, что похожим образом ломается и двойной хеш. Думаю, он напишет об этом. Остается выбирать рандомные множители.
Спасибо Макс, познавательно (хотя буду честным, пока что поленился вдаваться во все подробности :) ) Литература на эту тему может быть не известна или не существовать, потому как не брать по модулю а пользоваться переполнением — олимпиадный хак.
Кстати сказать, насчет олимпиадного хака Вы абсолютно не правы. Ровно тот же алгоритм используется в Java для хеширования строк, причем с основанием 31.
Только вот в Java никто не утверждает, что если хеши равны, то и строки равны.
UPD. А, HashSet валится этой штукой, что ли? Подумаю над этим.
Ну, по идее, вот тупой генератор строк с одинаковыми хешами, но для взломов он не годится — слишком медленный.
Мне сейчас пришла идея по поводу того, как генерировать строки намного быстрее, но это оставлю как задачу :).
UPD. Что, сине-зеленые минусовальщики, скинуть быстрый генератор? А хрен вам :).
Интересно. Спасибо. Посмотрел сейчас на свои хеши (я пишу немного не так, как на емаксе, поэтому была смутная надежда :) ), но они, разумеется, тоже падают. Не зря я хеши недолюбливаю.
Тогда уж
(под спойлером)
UPD: даже, есди быть точным, NOONONNOONNONOON!
Страшный сон великого и ужасного Хэшмэна.
Эх, чисто теоретически эти все взломы хешей безусловно очень классная штука.... Но теперь нормальному человеку, видя разумное решение с хешами, придётся что ли каждый раз извращаться что ли? Или надеяться, что автор не добавил тесты против хешей :( Не хочу ни на каком контесте даже двойные хеши писать... не вижу смысла.
Я думаю, что в правила хорошего тона при подготовке контестов вполне входит просто такого не делать. Здесь пожалуй есть исключение вида, "я хочу, чтобы задачу решали суффиксной стуктурой, а те кто пихают хеши пусть мучаются". Но такое скорее на пользу пойдет. Может люди научатся честно решать задачи. Правда проблема со взломами остается.
Мне казалось, что в правилах хорошего тона строить все разумные известные контрпримеры. Например, контрпримеры к жадным алгоритмам в задаче на ДП. Хеши по модулю 2^64, как оказалось, являются принципиальной ошибкой. Хорошим тоном кажется ДЕЛАТЬ такой тест.
Смотря где. В контесте со взломами обязательно. Об отношении к этому я уже писал, когда на меня ругались за AntiQuickSort. На тренировочных задачах тоже обязательно — чтобы люди умели бороться.
А дальше в зависимости от задачи. Если задача про правильное написание хешей — то да, надо. Если задача про суффиксную структуру, и вообще знать мы не хотим про эти хеши, то тоже да. Так их можно полностью отсечь, завалив два простых по TL например.
А если задача не про хеши, а про обрамляющее все это счастье структуру, то такие тесты явно ни к чему. Или если не дай бог нет онлайн-тестирования.
Не знаю, почему многие считают, что его надо брать простым — это ничем не обосновано.
Можно было бы и рассказать общественности: чем же на самом деле обоснован выбор основания. Ладно, расскажу сам.
Пусть модуль равен n, тогда по теореме Кармайкла мы имеем следующее: для любого a, взаимно простого с n, aλ(n) ≡ 1 (mod n), где λ(n) — функция Кармайкла. Здесь описаны утверждения о следующем: а) размер группы, образуемой степенями какого-либо числа по модулю n, не может быть больше λ(n), б) если для какого-либо основания a выполняется ab ≡ 1 (mod n), то b является делителем λ(n). Т.о. для проверки: подходит ли данное a на роль основания, нам достаточно проверить в качестве b все делители λ(n) (на самом деле, нам достаточно взять только простые делители pi и проверить степени λ(n) / pi).
P.S. То, что я написал выше, предназначено скорее всего для того, чтобы стимулировать заинтересовавшихся погуглить тему.
Вы имели в виду функцию Эйлера и теорему Эйлера?
Я имел в виду именно функцию Кармайкла и теорему Кармайкла. Фактически, теорема Эйлера есть частный случай теоремы Кармайкла (да, и φ(n) всегда делится на λ(n)).
а, вот как.
Все равно не очевидно как это связано с хешами. Что значит «подходит ли нам основание а»? И это а видимо должно быть простым по каким–то причинам?
a должно образовывать максимально большую мультипликативную группу по модулю n (если сказать просто: степени a должны иметь максимально большой период). И нам до лампочки, простое a или нет — главное, чтобы размер мультипликативной группы был в точности равен λ(n) (это всегда возможно).
Почему нужно к этому стремиться? Ну, хотя бы потому, что если период маленький, то коллизия подбирается без особых проблем. Пример очень плохого a для модуля 232: 65535 (зацикливается на 65536-ой итерации). А вот первые 10 "хороших" оснований из тех, что больше 27:
Понятно, спасибо.
Почти все нечетные числа будут хорошими. Чтобы уж точно быть уверенным, можно писать как-то так:
Зря я написал про уверенность, в связи с появлением этого топика теперь нельзя быть в чем-то уверенным :)
То, что вы написали, мне, конечно, известно. Только я эту фразу написал про выбор точки P в многочлене, а не про модуль — многие любят брать модуль 2^64 и в качестве точки простое число, зачем — непонятно, если все равно, как мы узнали, существует тест длины 2048, который все нечетные числа в основании выносит :-)
UPD: по теме порядков элементов по модулю 2^64 полезно еще знать, что 3 является почти-примитивным-вычетом (а примитивных вычетов, то есть порождающих своими степенями все нечетные числа, нет вообще). А значит и любая степень 3^k при нечетном k будет "хорошим" основанием для хеша. Так что можно не задумываясь брать 2187 — по модулю любой (достаточно большой) степени двойки 2^n период его степеней равен 2^(n-2).
Прошу прощения за ответ на комментарий пятилетней давности, но хотя бы ради будущих читателей хочу заметить: разве рассказ про функцию Кармайкла не относится как раз к точке (она же основание), а не к модулю?
Если зафиксировать модуль, то мы хотим подобрать такую точку, которая максимизирует длину периода степеней этой точки по этому модулю. Не любая точка это делает: например, при простом модуле 17 точки 3, 5, 6 и 7 дают период максимальной длины 16, а точки 2, 4, 8, 9 и 13 (простое число!) дают более короткие периоды с длиной соответственно 8, 4, 8, 8 и 4. Так что даже простая точка — не гарантия успеха!
Насколько я понимаю, если мы, например, генерируем точку случайно, то проверить её пригодность мы можем, возведя её в степени, являющиеся делителями λ(M) (где M — наш модуль), и убедившись, что ни одна из них не сравнима с 1 по модулю M.
главное, что бы теперь ребята из Екатеринбурга организовались, и почистили эту табличку (:
Эта задача замечательно решается без хешей за NlogN
Блииииииин!
Вот и первый радостный отзыв.
А сейчас есть решения с хешами? Это одиночные хеши, чудом избежавшие коллизий?
Я сделал вывод, что двойной хеш совершенно точно валится по TLE, а одиночный совершенно точно натыкается на коллизии на 3 тесте. Думаю, 3 тест это просто рандомная строка из 5000 символов.
P.S. Пойду наверно читать как нормально делать суффиксный массив...
Зачем? Там же есть очевидный квадрат на 10 строчек.
Ну я его не придумал
Hint: use KMP ;)
Я умею используя ничего. Просто один массив и два цикла :)
Ну не умеют люди писать суфмассив за квадрат, что поделать :-)
С поддержкой LCP? Не поделитесь умением? :)
Проблема в умении насчитать LCP в суфмассиве за квадрат? Хм...
Да, с LCP затупил. А какой метод построения за квадрат Вы имеете в виду? В мой уставший мозг лезет только сортировка по первой букве и рекурсивный вызов от образовавшихся групп.
А зачем суффмассив? Можно и просто так LCP всего насчитать.
Что поделать, умею только за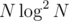 хешами. Пойду нормальный способ разбирать.
хешами. Пойду нормальный способ разбирать.
Умею за квадрат динамикой, но там квадрат памяти :)
Да-да. Именно так. А дальше храним два слоя.
N^2 log N, тоже самое, только строки сравнивать втупую:) — наше все.
Можно на самом деле хранить все состояния динамики. Значение lcp не превосходит длины строки. А она не превосходит 5000. Если юзать short вместо int'a все проходит по ML.
Решения на хешах есть. Но чтобы найти одно (с двойным хешированием, кстати), мне пришлось пересмотреть несколько десятков нормальных. Причём большая часть решений — "очевидный квадрат на 10 строчек".
На Java решений с хешами, наверное, не осталось, если такие вообще были. Я прав?
Были.
А теперь я не уверен, что C++ные остались.а не, говорят, что остались.Похоже на то. По крайней мере, среди работающих дольше, чем 0.5, их нету. Более быстрые не смотрел, но среди них тоже вряд ли есть.
Ну не, запихивается, если захотеть, даже на Джаве с двойным хешированием. http://acm.timus.ru/status.aspx?author=108910
Дай исходник :)
Чего там организовываться-то?
Странно. Почему-то не верится, что всего 53 решения с хешами было, с учетом того, что это дают как задачу на хеши в ЛКШ уже несколько лет...
Тем не менее, так оно и есть. Я сейчас выборочно полистал выжившие решения — там полное разнообразие. В основном квадратное дп или суф. массивы. Ну и изредка попадаются хеши по простым модулям, которые на этом тесте не валятся.
Кажется, что многие ещё не смогли упихать решение на хешах — из попадавших многие были на грани. Так что 53 из 666 не так и мало.
Я считал из 1161. Ну да. Из 613 это более адекватная цифра.
Кто-нибудь умеет ломать такой хак: использовать в качестве хеша пару из полиномиального хеша и первого символа строки?
Если к двум строкам с одинаковым значением полиномиального хеша дописать один и тот же символ в начало/конец, то хеши останутся одинаковыми.
Упс.
И, кстати, поэтому не работают всякие "выберем еще 10 случайных букв" и "разрежем в случайном месте" — можно добавить по очень большому одинаковому префиксу и суффиксу и тогда вероятность попасть в эту маленькую строку будет очень мала
Работает иногда конечно. В суффиксе как раз проблема в том, что он должен быть большим. Кто-нибудь знает грязный простой хак против этого теста, чтобы восстановить былое могущество?:)
И, подводя итог: Я подавлен. Теперь нет тупой уверенности в достаточности простых лонговых хешей.( Авторы могут издеваться над участниками, добавляя эти тесты (ведь не все слышали об этом, сделают на контесте еще хешей, только с другими основаниями, получат очередное WA, не сдадут задачу...) На мой взгляд, это скорей регрессивный тест: хеши есть, были и будут. Просто теперь нужно удовлетворять необоснованный садизм авторов.
Эм, почему работает то? Обычно ограничение на длину 100к, попасть в строку длины 211 вероятность около 1/500. Я с удовольствием буду челлнджить если вероятность успеха — 499/500 (и 49/50, если 10 букв)
А так — еще раз подтверждается, что иметь библиотеку — это хорошо
Про челлендж не понял.( Это про какой из вариантов?
Про библиотеку у меня свое мнение: я не уважаю это дело, библиотеку свою на контестах не использую. Я считаю, что это нехилый чит, и на нормальном соревновании подобного инструмента ни у кого не будет.
Про любой. Я не знаю способа сделать хеши по модулю 2^64 так, чтобы это не ломалось этим тестом/его простой модификацией
Про библиотеку — чит — это нарушение правил/норм морали. А по поводу нормальных соревнований — а что мы считаем нормальными соревнованиями? ACM ICPC и только его?
Да, разобрался. В моем предложении ключевым словом было: "иногда". Можно взять сильно больше рандомных цифр (опять же встречаем тл, только хэш с модулем работает быстрее, чем проверка тысяч букв:) ). Здесь фича в том, что на месте коллизии не совпадает много букв, и это нужно использовать. Если кто-нибудь придумает — в моем мире восстановится гармония.)
Ну, по поводу библиотеки я лишь высказал свое мнение. Я пока что был только на vkcup, и там сложно было использовать prewritten code.) Мне казалось, что на всех онсайтах возникнут некие проблемы с библиотекой. Я ошибаюсь?
На GCJ разрешено приносить с собой на флешке/выкачать до начала контеста из Интернета все, что угодно. На HackerCup вообще открыт доступ к Интернету во время контеста. На ТСО ничем пользоваться нельзя, но там даже IDE нету
Значит ошибаюсь. Но в силу моральных убеждений использовать ее не хочу:) Лучше лишний раз напишу за 10 минут, потренируюсь на будущее)
А в чем эти моральные убеждения? Я вот никак не могу понять. А использование IDE — морально приемлимо? А различные функции генерации кода в IDE? В чем именно проблема с библиотекой?
Prewritten code (в электронном или бумажном виде) разрешён на всех серьёзных контестах, кроме topcoder'а (там ещё буквально в блокноте надо код писать), OpenCup'а (но видимо многие читерят), SN*S и NEERC'а. Почему на вконтакте его запретили — непонятно.
А скилл "писать в 100500ый раз то же самое" в реальной жизни скорее вреден, чем полезен.
Кстати, в OpenCup со следующего года и в SN*S уже некоторое время этот запрет снят
Я верю в то, что в момент написания контеста у всех должны быть равные условия. У кого-то есть библиотеки, у кого-то нет. Согласен. что аргумент в пользу бедных:) Также в любом алгоритме, сколько десятков и сотен раз ты бы его не писал, можно набагать. А соревнования по программированию по большой части состоят из необходимости писать код. Поэтому библиотека дает ее хранителю меньше шансов набагать.
У всех были равные возможности написать библиотеку до начала контеста. Этак надо всем еще одинаковые компы раздавать, одинаковые IDE (или их полное отсутствие) и разрешать только один язык
Компы обычно дают одинаковые. Язык каждый выбирает сам из одного списка. Я думаю, что эта дискуссия бесполезна. Я лишь считаю, что любое соревнование по программированию — это соревнование мозгов и рук, а не времени, потраченного на удобный интерфейс.
То есть в том числе соревновании времени потраченного на никому не нужное в реальной жизни умение писать 100500 разных алгоритмов "наизусть" (ведь это будет быстрее чем у того, кто в алгоритме разобрался и пишет именно по памяти сути алгоритма)?
Да, таково соревнование.
Элементарно: подобрали произвольную коллизию и приписали к ней в начало произвольную букву.
Теги порадовали. Да и тема тоже. Всегда бесили хеши, примененные не по делу. Это ты после того как случайно нарвался на коллизию на обычном тесте решил исследовать?
Хорошо, что ты не видел, как мы решили J с ГП Азова :).
Свербило, понимаешь, после того случая в ЛКШ трехгодичной давности — решение падает, а объяснить никто не может, в чем проблема.
In POI19 http://main.edu.pl/en/archive/oi/19/pre ... It also contain such a case ...
We found that case by accident during that POI :) We actually submitted a short paper about this to the next IOI journal.
Кто нашел лопату??
Тссс! :-)
фишка взята у Alex_KPR?
Вот такое кто-нибудь умеет ломать? (FIRST_MOD и SECOND_MOD случайные, см. AbstractStringHash)
Думается, что
System.currentTimeMillis()надежно защищает — все методы нахождения коллизий основывались на явном знании хеш-функции. Собираюсь именно так писать, и, наверное, еще лучше иMULTIPLIER-ы рандомными сделать...Это, к счастью, ломать еще не научились... Но оно же медленное, там модули.( Да, и зачем два хеша? Коллизия встречается куда реже, чем тл.
Для коллизии c модулем порядка 10^9 достаточно порядка 10^5 строк. Поэтому 2 это строго обязательно
Да, все время забываю, что модуль не 2^64.)) Тогда все логично. :)
Для случайных чисел — см. эвристическое опровержение взлома здесь. Если числа будут не случайны — там есть генератор.
Ну, я привел конкретную реализацию ;) И модули — случайны, да
Количество "проверок хеша" одной строкой (при простых модулях) ограничено как минимум кубом ее длины, и построить тест с кубом ужасно сложно. В целом, кажется, что если имеется хотя бы 10^20 возможных хешей, то строить контртесты невозможно.
Если размер множества значений хорошей, сулчайной хэш-функции — X, то при sqrt(X) взятых случайных элементах, вероятность коллизии — уже . Разве ты не помнишь, как про это Gassa на сборах рассказывал? Поэтому нужно юзать либо лонг лонги (но это, как мы уже узнали, бессмысленно без взятия по модулю, а с ним в int64 можно оперировать только с числами до 2^32 потому что иначе произойдёт переполнение при умножении), значит приходится работать с парами лонг лонговых хэшей.
. Разве ты не помнишь, как про это Gassa на сборах рассказывал? Поэтому нужно юзать либо лонг лонги (но это, как мы уже узнали, бессмысленно без взятия по модулю, а с ним в int64 можно оперировать только с числами до 2^32 потому что иначе произойдёт переполнение при умножении), значит приходится работать с парами лонг лонговых хэшей.
Это будет чёрте-во-сколько раз медленнее, но зато не будет валиться таким тестом. Действительно, ты правильно сказал, это регресс-тест во всех отношениях.
Ну, не черти во сколько — мы же не будем это счастье хранить как пару — можно же в один лонг записать. А 2 взятия по модулю на подсчет хеша — не смертельно
Как-то я это пропустил...( Наверное, смотрел на монитор и восхищался:))
Наверно, можно без потери "невзламываемости" убрать взятие по модулю в одном из хешей.
Да, это полезно. Когда в ПЗ буду что-то с хешами пихать, это поможет.
Возможно. Но тогда я потеряю возможность всякие хорошие вещи считать типа хеш функции конкатенации двух строк
Речь о том, что один из хешей все-таки можно считать по модулю 2^64.
Я понимаю о чем речь. Если у меня два хеша запиханы в лонг (один сдвинут на 32 бита), то я могу извлечь оба значения и на этом основании делать всякие полезные вещи типа хеша конкатенации. Если один из хешей остается 64битным, то извлечь из одного лонга оба хеша я не смогу
Если по 2^64, нельзя будет эти два хеша засунуть в один лонг, а это клево.
Можно — xor'ом. Но извлечь потом нельзя будет, да
Почему? у вас просто один из модулей станет равен 2^32. А так никакой разницы.
С 2^32 надо быть крайне осторожным. Возможно, после этого можно будет просто "заспамить" второй хеш парадоксом дня рождения, поскольку построение выше требует только 2^8 длины.
Да, логично. На злополучном тесте у нас по сути остается один хеш. А это опасно. На всех остальных ничего не меняется. Тогда с 2^64 те же проблемы. Или я что-то напутал?
P.s. про "построение" не понял.
С 2^64 не должно быть проблем, так как у нас все-таки будет мало строк с совпадающим хешем по модулю степени 2ки — все таки каждая занимает 2048 символов, а не 256
Теперь понял про "построение". Да. логично. В общем, стараться не париться и использовать модули:)
Идею надо достраивать, но как минимум:
а) сделаем из этого теста 12 коллизий на один хеш, преобразовав его в коллизию 13 буква алфавита и строка из {12,14}, {11,15}, {10,16} и т.д. буквы алфавита.
б) будем писать соответствующие строки на каждое 8-ое место. Получим примерно 1500 коллизии с одинаковым хешом длины 2^11
в) конкатенируем их
После этого мы будем иметь уже 1500^2 "чистых" проверок второго хеша. Вероятность пока мала, но, скорее всего, все можно сделать и покруче.
Да, это вариант, хотя там появится много возможностей набагать. Я имел ввиду именно если мы один из хешей оставляем по модулю 2^64
Кстати, одно важное уточнение — генератор ни в коем случае не должен выдавать одинаковые FIRST_MOD и SECOND_MOD.
Он выдает случайное простое от 10^9 до 2 * 10^9 (вероятность каждого числа пропорционально числу составных до него). Я готов принять такой риск ;)
Кстати, надо быть и со встроенным ГСЧ осторожным. Были попытки (удалась бы, если не бага в API) создать копию ГСЧ, инициализированного временем в миллисекундах (бот Pifia для соревнования программ в Казани). Правда, на Codeforces это крайне сложно из-за нескольких проверяющих серверов.
Заметим, что для разницы времени 10 секунд у нас не более 10к вариантов ГСЧ (!)
Upd. Как минимум, необходимо использовать System.nanoTime() для инициализации ГСЧ.
Еще лучше — инициализировать при помощи SecureRandom.
Хаха, там бага была — вычитание с просто взятием по модулю. Теперь уже вроде нету
Надеюсь статью на e-maxxe обновят, а то как писать стало не совсем понятно.
KungA не читатель, KungA писатель? В комментах Егор даже готовый код выложил.
Кратко: решайте задачи так, как будто Вы никаких хешей сроду не знали.
А если без хэшей не решаются, то они — плохие задачи!
Было бы интересно увидеть пример такой задачи. Слышал про что-то такое, но навскидку ничего не получается придумать.
196D - Следующая хорошая строка
Мне кажется, без хешей ее решить заметно сложнее.
Ну что угодно двумерое, например. Найти количество различных подматриц размера k на k в матрице n x n.
Или уметь отвечать на запросы в онлайне — изменить символ в строке и сравнить две подстроки лексикографически.
За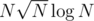 же легко делается. Даже за
же легко делается. Даже за 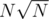 , но уже не на халяву.
, но уже не на халяву.
Ну а с хешами делается за n log n деревом отрезков нахаляву :-)
UPD: Опсь, log n на запрос, конечно, изменения. Запрос сравнить строки лексикографически за log^2 n.
UPD2: А за сколько у тебя, ещё раз, каждый запрос? Я тоже умею разбиением на блоки по корню за чистый корень относительно просто решать вообще без хешей. Слушай, ты прав, плохой второй запрос, log^2 от sqrt всё-таки не так сильно отличается. Давай считать, что после этого идёт запрос "проверить, совпали ли две выбранных подстроки в строке".
UPD3: Не, всё-таки исходную задачу я тоже за log n умею решать на оба запроса :-)
У меня такое решение. Пусть у нас есть суфструктура, которая умеет за O(f(N)) находить lcp двух подстрок. Это делается за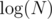 легко и за константу сложнее. (Кстати, можно как-нибудь находить lcp в онлайне за O(1) без извращенного LCA за O(1)?). Будем перестраивать эту структуру каждые
легко и за константу сложнее. (Кстати, можно как-нибудь находить lcp в онлайне за O(1) без извращенного LCA за O(1)?). Будем перестраивать эту структуру каждые 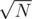 запросов, допустим, за линию. Теперь в каждый момент времени любая подстрока состоит из не более чем
запросов, допустим, за линию. Теперь в каждый момент времени любая подстрока состоит из не более чем 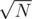 тривиальных подстрок (тривиальная подстрока — это либо один символ, который мы меняли, либо подстрока, в которой нет измененных символов). Значит, lcp любых двух подстрок мы можем найти за
тривиальных подстрок (тривиальная подстрока — это либо один символ, который мы меняли, либо подстрока, в которой нет измененных символов). Значит, lcp любых двух подстрок мы можем найти за 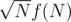 . Ну, а зная lcp, можно и лексикографически сравнивать, и на равенство. Хочется сказать, что у меня изменение работает за константу, но это не так — все-таки стоимость изменения входит в стоимость перестраивания структуры.
. Ну, а зная lcp, можно и лексикографически сравнивать, и на равенство. Хочется сказать, что у меня изменение работает за константу, но это не так — все-таки стоимость изменения входит в стоимость перестраивания структуры.
А как за логарифм и то, и другое делать? Без хешей, конечно.
Так я только с хешами умею за log n. Речь-то шла о примере задач, которые без хешей быстро не решаются.
http://acm.timus.ru/problem.aspx?space=1&num=1297
http://acm.timus.ru/problem.aspx?space=1&num=1354
http://acm.timus.ru/problem.aspx?space=1&num=1393
http://acm.timus.ru/problem.aspx?space=1&num=1423
http://acm.timus.ru/problem.aspx?space=1&num=1486
http://acm.timus.ru/problem.aspx?space=1&num=1517
http://acm.timus.ru/problem.aspx?space=1&num=1590
http://acm.timus.ru/problem.aspx?space=1&num=1684
http://acm.timus.ru/problem.aspx?space=1&num=1713
http://acm.timus.ru/problem.aspx?space=1&num=1732
Удачного вам реджаджа.
Вообще, такой сарказм у них в автоматической рассылке.
One or more of your solutions were rejudged. We apologize for wrong verdicts.
Свободу выбора они уже перетестили...
ой-ой-ой, надеюсь 1486 так не ломается
С ней чуть сложнее — за счёт малых линейных размеров совсем втупую она не ломается. Но я постараюсь решить эту проблему.
Спасибо, я и сам умею делать выборку по тегу. Реджадж тысяч сабмитов — дело неспешное, так что затянется это ещё на несколько дней. Но без внимания ничего не останется, так что можете начинать писать правильные решения.
Мне не e-mail почему-то не пришла новость о том, что мое решение упало из-за реджаджа, раньше вроде приходило.
А мне пришло. Может в спаме?
Остальным приходят. Проверьте настройки антиспама.
Проблема оказалась не в спаме, но она обнаружена. В любом случае спасибо.
Мне кстати тоже не пришло.
Упс. Видимо проблема в почте @gmail.ru. Sorry.
По задачам 1423 и 1354 зашли решения вида "если хэши совпали, то честно сравним подстроки". По-видимому, это вызвано тем, что в этих задачах мы ждем лишь одного совпадения подстрок, и общая проблема так не решится, но в некоторых задачах такой хак, кажется, катит...
В 1423 (равно как и в 1590 и некоторых других) можно считать хеш как он должен быть: используя sliding window и, соответственно, по большому модулю(порядка 1017), так как нам не нужно перемножать хеши.
Я считаю что тимус это архив задач с тестами взятый с реальных контестов, и добавлять туда тесты это жестоко. Таким путем например можно добавить новые тесты ко всем задачам на кф, а потом пересчитать все рейтинга начиная с 7 раунда. Или перетестировать задачи с реального соревнования и перераздать дипломы.
Тимус — для подготовки к будущим соревнованием. И что тогда, если такой тест додадут к какому-то соревнованию?
На четвертьфинале 2006 года (это начало 6-го тома) баги были почти во всех задачах. В контестах до этого было получше, но не везде и ненамного. После этого программный комитет и контесты стали готовиться на порядок лучше, но тем не менее. На четвертьфинале 2008 года участники пропихивали жадину, контрпример к которой я построил сразу после контеста. На чемпионате УрГУ 2010 года авторы на разборе рассказывали жадину, контрпример к которой построили уже на следующий день. На четвертьфинале 2011 года в одной из задач были вообще некорректные тесты, что заметили только на последних минутах соревнования.
Это я всё к чему. Реальные контесты — штука хорошая, но не всегда и не во всём они отражают умение нормально решать задачи. А уметь пропихивать ботву может быть полезно разве что на совсем локальных контестах, где нет опытных проблемсеттеров и где бывают слабые тесты. Поэтому мы регулярно проводим работу по исправлению старых задач, усилению тестов и т.п. Именно ради того, чтобы пользователи учились решать задачи, а не пропихивать ботву. Иначе мы бы так и оставались на уровне начала 2000-х, когда контесты выигрывали те, кто лучше придумывал эвристики, а не те, кто лучше придумывал правильные решения.
Я на РОИ в этом году ботву на 100 пропихнул)
На РОИ кто только не пихал ботву на 100
Гена, например, никогда не пихал ботву на РОИ ;)
Зато я в этом году запихнул. Cамую простую задачу второго дня с линейным решением запихал за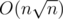 :) При этом валится каким-то простым рандомом
:) При этом валится каким-то простым рандомом
Про свой квадрат, методом, перебрали за линию величину, а потом внутри посчитали ее за линию еще раз год назад, я лучше и вспоминать не буду. Кстати тоже запихнулся.
Специфика уральских контестов, так обожаемая в Петрозаводске...
Никто не пересчитывал результаты реальных соревнований на тимусе.
А на КФ вроде тоже есть задачи, к которым тесты добавлены.
1423, 1517, 1590 теперь фейл. А 1102, 1297, 1354 все еще AC(оказывается бывают и те дни когда мне везет:)). Следствием тем что на тимусе начали добавлять злобные тесты хотелось бы прочитать статью про бор. Не могли бы ссылку дать?
Обычный бор в качестве побочной темы описан тут. Насчет сжатого — погуглите на КФ, где-то даже валяется его реализация на С++ в моем исполнении.
Не читал весь пост (времени нет), но появились такие мысли: 1) что если вычисления делать не со стандартным переполнением, а по модулю большого рандомного числа который получается из текущего времени; 2) можно как всегда взять вектор модулей перегрузить для него операторы =, * и делать как обычно. И тот и другой вариант работают медленней, но уверен что заходят :-) UPD: Вообще думаю что это не тру валить хеши, ведь хеши всегда можно так подхачить что они пройдут (особенно при онлайн-тестировании). С другой стороны писать суф. структуры мне тоже очень нравится.
Проблема в том, что нам нужны модули сильно меньше чем раньше (<2^32), что заставляет считать по нескольким модулям, да и еще и брать по модулю. в итоге сильно медленнее.
Это уже обсуждали. Одним модулем не обойдешься, так как чтобы не было переполнений при умножении модуль придется брать не более чем порядка 2 миллиардов. Несколько случайных модулей катят
Вот http://acm.timus.ru/problem.aspx?space=1&num=1590, тут хеши без модуля с хэштаблицей работали у меня 0.937 при тл в 1, так что как сдавать теперь хэшами не представляю.
Напишите суфдерево/суфмассив/суфавтомат и не парьтесь. Зайдет с многократным запасом.
Ну неаккуратно код пишете, там сдаются двойные хеши на джаве.
Ты, собственно, описал единственно возможный способ исправить ситуацию с хешами. Почитай комментарии, тут много умных мыслей было.
По поводу "не тру валить хеши, хеши всегда зайдут" — речь-то как раз о том, что так, как испокон веков писали хеши все правильные олимпиадники, писать нельзя, потому что это всегда валится тестом длины 2048. И тут не подхачишь, гарантированно будет WA.
А что если каким-то костылем искать эту строку и если она есть, то считать для нее хэш по другому основанию?
Появилась такая мысль:
будем хэшировать почти как обычно, только прибавлять к очередному хэшу не просто код символа, а число, зависящее от текущего и предыдущего символа:
h[i] = h[i-1]*P + f(s[i-1],s[i]).
т.е. фактически считаются хеши "перегородок" между символами. Отдельно придется обработать случай подстроки из одного символа.
Можно ли это как-то сломать аналогичным тестом?
А как в данной модели считать хеш подстроки? Если не нужно хешей подстроки, можно проще: h[i] = h[i-1]*P + (s[i] + i) * (s[i] + i).
h[to]-h[fr]*p^(to-fr)
Ну вы де-факто что сделали — вы взяли, заменили каждый символ на пару (символ, следующий), тем самым добившись увеличения асимптотики построения хэша в два раза и добившись того, что контретест выше теперь является тестом на алфавите из четырёх символов (AA, AB, BA, BB).
Я одним местом чую, что достаточно будет увеличить длину теста максимум в четыре раза, чтобы он снова стал контртестом. Своему месту я доверяю :-)
Знаете, это может быть хорошей идеей, только если заменить константу 2 на константу k = 10, тогда размер нового алфавита вырастет экспоненциально и валить это станет, наверное, подобными тестами невозможно. Может попробуете написать и сдать, например, ту задачу, о которой идёт речь?
Это хорошая идея, но она требует замедления в k раз на стадии предподсчёта. Мне кажется, любые запросы к такой структуре выполняются за прежние O(1) по модулю коротких строчек.
То, что я предлагал проходит 1517 на тимусе. А где можно кубики сдать?
Хм. Наверное только скачать отсюда, питерская городская олимпиада, практический тур, задача E.
А задачу, на которой Петя упал, на этом тесте для Q = 22 (строка длиной 4 миллиона) проходит?
UPD: Да, и какую функцию f используете?
f — случайная перестановка чисел от 1 до 26*26. Еще заходила ((c1+3)*53)^(с2+7). Не проходили линейные вида с1*x+c2, скорее всего из-за того, что тогда, видимо, как-то можно представить в прежнем виде с другим множителем.
upd: в задаче палиндромность на тесте с Q=22 выдает 12 (решение vepifanov выводит то же самое).
Круто, что я могу сказать.
Кубики шляпа, там обычный хеш по модулю любому заходит, но всё же: http://www.e-olimp.com/problems/2173
Слушай, мы тут так посмотреть весь топик обсуждали, что хэш по любому модулю, не являющемуся степенью двойки, всегда заходит, тогда как по модулю 2^64 не зайдёт.
Ну человек попросил дать ссылку на кубики, я дал ссылку на кубики. 2^64 там не заходит, простой модуль заходит, то есть далеко не показательная задача. А в чём проблема?
Ну, вполне показательная задача. Топик-то как раз и гласит о существовании таких задач, где надо вместо модуля 2^64 юзать простой модуль, чтобы зашло :-)
Ок :)
1590 проходит? А то либо я криворукий, либо падает :(
проходит, правда у меня были проблемы с TL.
Если не нужно хэшей подстроки, то почти любая махинация будет работать. Достаточно будет взять набор случайных чисел A_0 ... A_(n-1) за коэффициенты того же самого многочлена и такой хэш будет уже не поломать.
Да вроде так же.
Строка какой взамывать:
для Q = 3 => ААВААВВВА, вроде так. То есть мы берем вот строку о которой пост, и когда в ней буква А следущую букву ставим равной превидущей, а когда В, то меняем на противоположную.
Вы упираете на то, что в его терминологии f(AA) = f(BB) и f(AB) = f(BA). Он же использует больше информации чем то, совпали ли две буквы или нет.
Ну да, ошибся.
А для первого символа f(s[0],s[-1]) какой?
для первого символа h[0] = 0, т.к. перед ним вообще нет перегородок.
А проходит тест, если на места == 0 (mod 4) записать тест выше, а на остальные буквы 'A' ?
Upd. И в начало и в конец приписать 10 букв 'A'.
В задаче 7D выдает правильный ответ.
генерил тест так (N = 1<<20):
upd: если дописывать по 5 букв A вместо 10, все-таки падает:(. Спасибо.
Похоже, что если брать функцию f от k подряд идущих символов то достаточно повставлять группы по ровно k штук из подряд идущих A-шек в контртест.
Получается, мы генерируем последовательность Морса-Туэ? Её, кажется, можно и как контртест к алгоритму Хаффмана применить.
Да, точно. Я названия сходу не вспомнил, но это именно она.
Если кому-то интересно, то можно почитать здесь:
http://ru.wikipedia.org/wiki/Последовательность_Морса-Туэ
http://en.wikipedia.org/wiki/Thue–Morse_sequence
http://mathworld.wolfram.com/Thue-MorseSequence.html
Sorry to revive this, but I use a lot of hashing technique for online contests and have some questions :).
In short, the solution to not be targeted by this anti-hash test is to use a different mod (not power of 2)? For instance using mod 10^9+7. But that mod is kind of small, and with around 50k random strings it is really easy to get a collision. Using a larger mod will require to implement a function to multiply longs, and that function adds an unwanted overhead to the solution that might make it time out easily on some problems (does knows an efficient way of doing it? I can only think of a O(bits) way, where bits is the number of bits of our mod, something like this: http://pastebin.com/r5Af5zfp).
One other possibility is using two mods (that fit in an int type), and creating a pair of hash values. My question is, is that enough? I mean, enough for online contests where there won't be more than 10^8 string hashes. Through some empirical results, I couldn't find a hash collision for that, my bruteforce test code is here: http://pastebin.com/iaVp6ypH (be careful running it, it can consume pretty fast your computer memory, adjust the LIMIT variable for your purposes). Thanks!
You are talking right things. Hash value of order 10^9 + 7 can really cause collisions. But it's useful to understand why exactly collision can happen.
Imagine the problem, where you are asked to check 105 pairs of substrings of big string to be equal. Suppose that answers for each query are in fact "NO". Let's assume that due to big length hash of each substring is random uniformly distributed value over segment [0..109 + 6] not depending from hashes of other strings. Then the probability that the check suddenly gives us answer "YES" instead of "NO" is almost same with the probability of two uniformly distributed values from that segment to be equal. This probability is 10 - 9. The probability that no one of the 105 checks will fail due to collision is (1 - 10 - 9)105 ≈ 1 - 10 - 4, that is really close to 1. One the testset consisting of 100 tests the probability that you'll recieve "Accepted" is (1 - 10 - 4)100 ≈ 99%. That's pretty big probability to write such solution, so using single hash modulo 109 + 7 is ok for that type of problems.
Other type of problems involve checks like "check that hashes of 105 substrings are pairwise different". For example if we calculate number of different substrings of length 5·104 in string of length 105 and they all are in fact different. Once again, we can assume that each hash of that substrings is random uniformly distributed value from segment [0..109 + 7], that are independent one for each other. So now we need to calculate another probability: that from 105 random integers from range of length 109 no two will suddenly coincide, giving as less answer then expected an verdict "Wrong Answer".
But here appears the effect known as Birthday problem: surprisingly, but for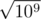 different independent randomly distributed values probability for some pair of the to be equal is about
different independent randomly distributed values probability for some pair of the to be equal is about  . So for 105 probes our probability to fail on one test will be even greater than 50%!
. So for 105 probes our probability to fail on one test will be even greater than 50%!
Here is one note: we take hash over prime modulo because for prime p Zp is a field, and for finite fields it can be proven, that all values above (that are values of random polynomials in fixed point) are very close to be really uniformly distributed over the whole field. If we take composite number, there will appear special effects like zero divisors and other, so there is needed additional analysis of probability for that cases, it can easily happen that all such calculations for them will be wrong. The main idea of my topic is exactly about surprising property of Z264, that one can easily build a polynomial of small degree (~2048), whose value is zero in any point, so it isn't suitable for solving problems with hashes.
So as you correctly said, we need to increase the hash-value space size. One way is to look on one hash modulo prime of greater size. But there is indeed a problem with their multiplication. You can multiply them with binary multiplication (such as binary exponentiation, but with adding and doubling on each step), or you can use some hacks like this (examples of code in Russian interface).
Other idea is two use a pair of hashes by two different prime modulo of order 109, let's say, p and q. Then we once again can assume that two components of that hash will be independent of each other random uniformly distributed over the Zp and Zq respectively, so in fact we have a point in 2d-space that is randomly uniformly distributed over the p·q ≈ 1018 possible values. Then in every calculation above we can replace 109 with 1018 and probability for us to fail becomes insignificant. From my experience this way is faster then previous two.
I hope this will help in understanding, when hashes can cause a collision, and why we can submit correctly proved hash solution and be sure, that it will be Accepted.
Wow, very complete response :). Thank you for the help, It definitely helped in understanding!! We should learn Russian, we miss so much interesting information only available at CF.ru posts :|
There is also a very interesting article here: http://www.mii.lt/olympiads_in_informatics/pdf/INFOL119.pdf A friend sent me, not sure if he found here on CF or somewhere else..
Look a few posts above and you will see one of the author of this article saying that they submitted a paper about this :D.
But note one other thing. Exactly as Zlobober said there are two types of problems where hashes are useful — comparing many pairs of strings and checking if all hashes are different. Note that when you just check if two hashes are equal or not, you probably won't have to check so many pairs that a probability of a collision will be high, because firstly it will rather exceed time limit than find a collision. In that case exponent in (1-p)^k (where p is a prob. of collision) grows linearly with time of execution. When you have 10^6 hashes generated modulo 10^9 number of colliding hashes will be pretty high but that doesn't change fact that if you won't do more than 10^6 queries of type "==" the probability of FINDING collision is really small (~0.999). This can be stated unless you won't do anything else than using operation "==" or "!=". But when you use other operations such as "<" the exponent and so the probability of collision may grow much faster! Best example is a simple example "are all of those hashes are different". You can sort them and check if every two consecutive values of hashes are different. But in this case you have used a specific values of hashes and that allowed you to obtain O(n^2) informations in O(n log n), so a probability of finding a collision in former example is very large.
So summing up:
I use only "==" and "!=" -> nothing to worry about
I use "<" (maybe hidden in sort or a set or a map or anything) -> use pair of hashes mod 10^9+7 and 10^9+13 or anything else.
// ЛОПАТА ибо нефиг копипастить во время контеста :-)
Интересно, сколько человек за два года обнаружили это, пытаясь скопировать код генератора? =)
Я вот на днях придумал такую штуку. Кто может поломать фибоначчевый хэш по модулю 2^32? Zlobober?
a_0 (0; 1) + a_1 (0, 1; b, 1) (0; 1) + a_2 (0, 1; b, 1) ^ 2 (0; 1) + …
Где a_i — буквы в строке, b — случайная нечётная константа, ';' — разделитель строк в матрице. Получается результат — вектор из двух int32. Вычислять такое можно по аналогии быстро для подстрок, только работать надо не с одним int64, а с двумя int32. Почему это фибоначчевый хэш? Потому что можно упростить умножение матриц: (0, 1; b, 1) (x; y) = (y; bx + y) — этот приём используется для подсчёта чисел Фибоначчи или аналогичных последовательностей.
Спасибо тем кто попытается взломать!
The same in English: I came up with a workaround. Can someone break a Fibonacci hash modulo 2^32? Zlobober?
a_0 (0; 1) + a_1 (0, 1; b, 1) (0; 1) + a_2 (0, 1; b, 1) ^ 2 (0; 1) + …
Where a_i — letters in a string, b — random odd constant, ';' — delimiter in a matrix. The resulting hash is a vector of two int32's. You can compute it for substrings analogically, but you need to work with two int32's instead of one int64. Why is it a Fibonacci hash? Because one can simplify matrixes multiplication: (0, 1; b, 1) (x; y) = (y; bx + y) — this trick is used for computing Fibonacci numbers and analogical sequences.
Thanks to everyone who will try to break it!
Strings "aab" and "bba" have the same hash value.
Thank you for your example, but I guess you didn't quite understand the idea. I'll try to explain in more details. The matrix notation (0, 1; b, 1) means two by two matrix:
a_0 (0; 1) + a_1 (0, 1; b, 1) (0; 1) + a_2 (0, 1; b, 1) ^ 2 (0; 1) = a_0 (0; 1) + a_1 (1; 1) + a_2 (1; b + 1)
We can assume that char 'a' code is zero and char 'b' code is one. Then hash("aab") = (1, b + 1) and hash("bba") = (1, 2). These hash codes are obviously unequal. I guess you thought that b = 1 because of the name 'Fibonacci'. But I meant extended Fibonacci sequence when x_n = x_(n-1) * b + x_(n-2)
You are right, I misread your comment, sorry :) This approach should work, given that b > max char value.
BTW, if we consider eigenvalues of (0, 1; b, 1) it seems that your hash is equivalent to the polynomial hash with base (1+sqrt(4*b+1))/2 in the ring of numbers of the form x+y*sqrt(4*b+1) (x, y taken modulo 2^32) when 4*b+1 is non-residue modulo 2^32 (which is the case iff b is odd).
Hmm, eigenvalues interpretation is interesting.
Sorry for necroposting, but this is possible to break as well.
I will consider slightly more general construction. Let M be some 2 × 2 matrix with integer coefficients then hash of string s0s1... sn is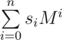 modulo 2w (w = 32 or w = 64) — also 2 × 2 matrix.
modulo 2w (w = 32 or w = 64) — also 2 × 2 matrix.
In your case,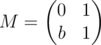 for some odd b. One can verify that M2 = M + b (b is a shorthand for bE, where E is the identity matrix) holds even in integers, let alone modulo any number (math remark: because M's characteristic polynomial is x2 - x - b). One can say that
for some odd b. One can verify that M2 = M + b (b is a shorthand for bE, where E is the identity matrix) holds even in integers, let alone modulo any number (math remark: because M's characteristic polynomial is x2 - x - b). One can say that 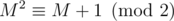 in the following sense
in the following sense 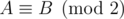 if A - B has only even entries. Therefore
if A - B has only even entries. Therefore 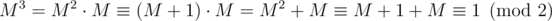 .
.
Now we can substitute M3 instead of P in the (P - 1)(P2 - 1)... (P2Q - 1 - 1) expression from the post. One can see that only important quality of P was that P - 1 and P + 1 are both divisible by 2. As shown above, in a sense this still holds for M3. Therefore (M3 - 1)(M6 - 1)... (M2Q - 1·3 - 1) is a polynomial of M with small degree, coefficients in range [ - 1, 1] and is zero on any matrix of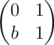 form.
form.
Even more, suppose that M is any 2 × 2 integer matrix with odd determinant (basically, nondegenerate when considered modulo 2). Then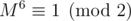 . One can verify this by brut force, but probably easier way to see this is (warning: math ahead) is noticing that nondegenerate matrices modulo 2 form a finite group of order 6 and apply [Lagrange's theorem, link is not clickable for some reason](https://en.wikipedia.org/wiki/Lagrange%27s_theorem_(group_theory)#Applications ).
. One can verify this by brut force, but probably easier way to see this is (warning: math ahead) is noticing that nondegenerate matrices modulo 2 form a finite group of order 6 and apply [Lagrange's theorem, link is not clickable for some reason](https://en.wikipedia.org/wiki/Lagrange%27s_theorem_(group_theory)#Applications ).
Considering matrices M that are degenerate modulo 2 may complicate things a bit, but this is not the best idea for the same reason as using even P is a really bad idea when using simple polynomial hashes modulo 2w.
Warning: more math ahead.
One can also ask what will happen if we use 3 × 3, 4 × 4 matrices, et cetera. Well, for 3 × 3 matrices and w = 64 the degree of the resulting polynomial will be 211·|GL(3, 2)| = 211·(8 - 1)·(8 - 2)·(8 - 4) = 344064 (you can read about GL(n, p) here), what is slightly more than usual constraints in string problems, but I believe that this can be hacked with more careful consideration of the same idea. And I am not sure that using 4 × 4 matrices will be faster than usual double hashing approach (did not test it though) and it doesn't sound safe either.
TL;DR: strings s and t generated by the following code should have equal Fibonacci hashes modulo 264:
This is very nice. Good observations!
In fact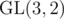 has no element of order 8 — either by bruteforce, or rational canonical form, or the observation that the (Heisenberg) subgroup of upper triangular matrices is a non-cyclic Sylow 2-subgroup, or (insert simple argument here) — so you can reduce the degree of your polynomial to 172032. I can't see how to reduce it further, since there are matrices of order 3, 4, and 7.
has no element of order 8 — either by bruteforce, or rational canonical form, or the observation that the (Heisenberg) subgroup of upper triangular matrices is a non-cyclic Sylow 2-subgroup, or (insert simple argument here) — so you can reduce the degree of your polynomial to 172032. I can't see how to reduce it further, since there are matrices of order 3, 4, and 7.
Actually the decision to use matrices seems a bit arbitrary, since multiplication is slow, and you're really only using powers of a single matrix.
We could instead use a ring of the form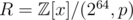 , where p is an arbitrary monic integer polynomial of degree d, say, with
, where p is an arbitrary monic integer polynomial of degree d, say, with 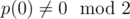 , so that x is invertible in R, and then let the hash of a be
, so that x is invertible in R, and then let the hash of a be 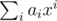 , evaluated in R. (Elements of R can be represented uniquely as
, evaluated in R. (Elements of R can be represented uniquely as 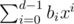 , where each bi is a long long.)
, where each bi is a long long.)
This is essentially equivalent to using d × d matrices, since any such matrix is a root of a polynomial of degree d (Cayley-Hamilton), and the minimal polynomial could be any polynomial of degree d (e.g. consider the matrix representing multiplication by x with regard to the basis 1, x, ..., xd - 1 of R).
However, each multiplication in R requires 'only' O(d2) long long operations, and each addition requires only O(d) long long additions, which is slightly better than the O(d3), O(d2) required for d × d-matrices.
For d = 4, according to my calculations the order of x modulo 2, i.e. in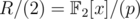 , is either 15, 7, 12, 8, or a divisor of one of them, so your hack would require a string of length 211·5·3·7·8 = 1720320, assuming you don't know p.
, is either 15, 7, 12, 8, or a divisor of one of them, so your hack would require a string of length 211·5·3·7·8 = 1720320, assuming you don't know p.
If the hacker knows the order m of x mod 2, however, they will only need length 211m. The fact that m seems to inevatibly be fairly small suggests that this approach is essentially no better than say choosing a small number m at random, dividing the string into chunks of size m, and treating each chunk as one character somehow.
Tl;dr: Just use one or more large primes.
By the way, order of any element of GL(d, 2) does not exceed 2d - 1 (simple proof here). Therefore m ≤ 2d - 1 always holds and m always is quite small.
UPD. So hacker can just generate a pair of strings with same hash for every possible "maximal" m ≤ 2d - 1 (i. e. m is a divisor of |GL(d, 2)| and does not have multiples less than 2d other than itself). Their total length won't be very big even for d = 4 and their concatenation would work as countertest in most problems.