
English version:
The first problem is similar to Problem G — Inverse Factorial in 2016 ICPC North American Qualifier Contest; however, there is a twist: if there is no n for the given value n!, you need to output - 1.
I think there is a solution for this problem, but I can not find it :)
By the way, a gifted 9-grader in Vietnam has no idea about FFT anything similar to that.










There is some limit (10^6) given in the problem. Is it for n or for n! ?
It is for the number of digits of n! :)
I don't think even FFT can solve this problem in time.
PS: Just figured out that you can calculate x! quickly with divide and conquer + FFT (or Karatsuba) in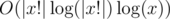 (|s| is length of s). Still, this is too insane for 9-grader problem. (This would have Div 1-D level of difficulty). I wonder if there is a simpler way to check the solution.
(|s| is length of s). Still, this is too insane for 9-grader problem. (This would have Div 1-D level of difficulty). I wonder if there is a simpler way to check the solution.
Several comparison with modulo prime will be not bad. (simillar to hashing)
Still, that is a bad problem.
There is an easy soln to this problem: Notice that when n>=10, then no. of digits in n! < no. of digits in (n+1)!(Common Sense, can also be proven mathematically). Now you can count the no. of digits in n! in this way — http://www.geeksforgeeks.org/count-digits-factorial-set-1/
Now, you can binary search for the value of n. For n < 10 you can check it using brute force. To check if ans is -1, there will be exactly one value of n for which you need to calculate n! (after doing binary search), use python :P, or as koosaga said, use several comparisons with prime modulos.
How would you check if n! indeed equals the given number if number of digits are same but possibly, there is no solution? (using modulo primes?)
I have edited my comment above, please refer to my comment above :P, you can also use multiple modulo primes, as stated by you.
We all know how to do it. We just don't know how to do it "in time" (instead of your n^2 algorithm)