bvd's blog

A hard problem from Vietnam Olympiad in Informatics for 9-grader [Part 2]
By bvd, history, 8 years ago, In English

17493195_1919527948281479_2748595590774946471_o.jpg

English version:

The first problem is similar to Problem G — Inverse Factorial in 2016 ICPC North American Qualifier Contest; however, there is a twist: if there is no n for the given value n!, you need to output  - 1.

I think there is a solution for this problem, but I can not find it :)

By the way, a gifted 9-grader in Vietnam has no idea about FFT anything similar to that.

  • Vote: I like it
  • +3
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

There is some limit (10^6) given in the problem. Is it for n or for n! ?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It is for the number of digits of n! :)

    → Reply
»
8 years ago, # |
← Rev. 7   Vote: I like it 0 Vote: I do not like it

I don't think even FFT can solve this problem in time.

PS: Just figured out that you can calculate x! quickly with divide and conquer + FFT (or Karatsuba) in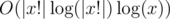 (|s| is length of s). Still, this is too insane for 9-grader problem. (This would have Div 1-D level of difficulty). I wonder if there is a simpler way to check the solution.

→ Reply
»
8 years ago, # |
  Vote: I like it +13 Vote: I do not like it

Several comparison with modulo prime will be not bad. (simillar to hashing)

Still, that is a bad problem.

→ Reply
»
8 years ago, # |
← Rev. 5   Vote: I like it 0 Vote: I do not like it

There is an easy soln to this problem: Notice that when n>=10, then no. of digits in n! < no. of digits in (n+1)!(Common Sense, can also be proven mathematically). Now you can count the no. of digits in n! in this way — http://www.geeksforgeeks.org/count-digits-factorial-set-1/

Now, you can binary search for the value of n. For n < 10 you can check it using brute force. To check if ans is -1, there will be exactly one value of n for which you need to calculate n! (after doing binary search), use python :P, or as koosaga said, use several comparisons with prime modulos.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    How would you check if n! indeed equals the given number if number of digits are same but possibly, there is no solution? (using modulo primes?)

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      I have edited my comment above, please refer to my comment above :P, you can also use multiple modulo primes, as stated by you.

      → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    We all know how to do it. We just don't know how to do it "in time" (instead of your n^2 algorithm)

    → Reply