Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 166 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 160 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
| Название |
|---|



In div1 B, preprocessing all relevant factorials and also their modular multiplicative inverses modulo 109 + 7 can be in O(n) even if we don't consider the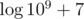 a constant :)
a constant :)
How can we calculate modular multiplicative inverses of factorials in O(n) for inverse we will need logN
Like this? first calculate ifact[MAXN] , then ifact[x-1]=ifact[x]*x ?
oops, sorry I can't read.
Yes, this is an efficient method in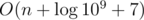 , and I prefer it to the following O(n) method:
, and I prefer it to the following O(n) method:
rev[i] = -(MOD / i) * rev[MOD % i](whereMOD= 109 + 7), and thenifact[i] = ifact[i - 1] * rev[i].Anyway,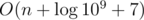 is very close to O(n) and much smaller than
is very close to O(n) and much smaller than 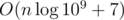 .
.
In "Karen and Test": We will repeatedly perform the operation until the number of elements n is even, and the first operation is addition, ... this will happen somewhere within the first 4 rows.
Even better, it will happen within the first 2 rows. If n is even, it has already happened. If n is odd, we only need to do one iteration. The second line will have an even number of elements, and the first operation will always be "+". That's because the first line has (n-1) operations, which is an even number, so the first operation in the second line is guaranteed to be "+".
Really awesome editorials along with pictorial representations <3
Div.2 B was really nice, there is more than a dozen of approaches to solve this task :D
In div1 E, I used binary search. Fix k and divide the segments to three sets(left, right, middle). The remaining part is easy. Time complexity is O(log^2 n).
http://mirror.codeforces.com/contest/815/submission/27895623
Thank you. Your solution is much easier to understand and implement for me compared to other solutions of Div.1 E .
Can you please elaborate what your solution does ?
Nice contest and editorial, too. However, the following makes me a bit sad:
Actually, there is no upcoming contest in AtCoder too. It's so sad...
There is a contest in csacademy, and hackerrank. I believe that there are a lot of other contests in other websites.
I do not know if it is a notorious coincidence :P When I have my holidays,CF rounds are so rare but during my semester exam time ,They are quite frequent :(
Can inclusion exclusion be used for Karen and cards?
I used event sorting for my DIV2 B solution but i think i like the solution of the problem setter. Simple and interesting.
Please hide this anime bullshit. Codeforces is not an anime site. I don't want to see these pictures when I read an editorial.
Please hide this hate bullshit. Codeforces is not a hate site. I don't want to see these comments when I read an editorial.
Understandable. The editorial is already quite long, and adding the pictures just makes it a bit longer and less readable. They should be removed in a while.
Have a great day!
Nooo, don't. I like the pictures
But I see no picture on the editorial......
Nice explanations! I liked the reduction presented in 2D's editorial.
In Div2D/Div1B[editorial] what does the K represent?
The index of the element in the sequence.
For Div1B, I'm very curious why we can always reduce it to the "addition" version of the problem. In contest I failed to find a proof for it, and the editorial only mentions some pattern finding, which is way far from proving it. Is there any Div1B level proof for it?
I'm not quite sure what you mean by reducing it to "addition" version of the problem. If you start with addition then after applying the operation four times, you'll do n - 1 + n - 2 + n - 3 + n - 4 = 2(2n - 5) additions/subtractions in total, so if you start with addition, after four rows the first operation will also be addition.
Well sadly, I also can't understand what you are saying, too..
Whatever, Let me rephrase what I meant. Author claims :
The problem with only plus operation is easily solvable with fast algos.
After 4k-th iteration, The problem with only minus operation actually become an instance of "The problem with only plus operation", with input as odd / even array element. So we can perform 4[n/4] operation very fast.
I agree on first paragraph, and pattern shows second is true, but I'm not sure why.
UPD : Ok now I got it. I didn't read the part that we always reduce it to + / even n case. Now we can prove it. I'm sorry, and thank you for the help!
What I was trying to say is the pattern always repeats itself every four rows so the pattern will continue.
Yeah! After a long time waiting
In div 1 C. How does the sum converge to O(n)?
I have the same question bro Why no one answered you q.q
Isn't Div1E effectively this: https://code.google.com/codejam/contest/3264486/dashboard#s=p2 ?
It's not exactly the same. However, both are similar to problem I proposed at Croatian Olympiad in Informatics 2 years ago (http://hsin.hr/2015/olympiad/tasks.pdf; OGLEDALA).
Also, the story of GCJ one is similar, but it's understandeable, as the inspiration obviously comes from real life — urinals. I don't remember why we changed it to washbasins in my problem, though.
Ha, speaking of urinals: http://www.spoj.com/problems/URI/
And if I'm not mistaken, this is actually exactly the same as Div1E. (I'm problemsetter for the SPOJ problem). Too bad I did not participate in the round :D
In div1 C, the naive dp actually works in N^2 if you don't take j and k all the way up to n every time but only the amount which is actually possible in those subtrees.
Will you please explain how it runs in O(n^2) .
Initially you have the size of 1. When you get a subtree of size S you'll make a S * size transition and then you'll make size += S. On the first step, you'll pair the current vertex with all the vertices from the subtree. From the second step onwards, you'll pair the current vertex AND the already counted vertices with the vertices of the next subtree (the number of such pair is S * size). This means that you'll never count any pair twice and the complexity will be exactly the number of such pairs, or O(n^2)
To be pricise,you can calculate the complexity is this way: just a sketch:
s[1]*1+s[2]*(1+s[1])+s[3]*(1+s[1]+s[2])+...=sigma(s[i]*s[j])=[(sigma(s[i]))^2-sigma(s[i]^2)]/2
adding each iteration together,you will find all terms except n^2 will cancel each other So in total,complexity=O(n^2)
Here, you have calculated the time complexity of finding f values for a single node and it turns out to be O(n^2). It may still become O(n^3) when you sum it over all the nodes.
No.
As I explained above, for each iteration(say node v), the complexity is O((number of sons of v+1)^2-sigma(size of each subtree of v)^2) =O((size of tree rooted at v)^2-sigma(size of tree rooted at a son of v)^2)
When adding these complexity together, we get O(n^2),where n is the size of tree rooted at 1, as all other terms will cancel each other. (according to the problem statement ,each node has only one father;and of course each node is the root of a unique subree)
How come my this solution is not passing then, which is IMO exactly as per the algorithm which you have shown to be O(N^2). It's TLE(ing) on 27th test case.
Thanks a lot .
I tried the question DIV1 C using the approach you have suggested but I'm getting TLE and to me, it seems like the complexity of my code is O(n^2 * logn) and for the given constraints it should be enough but still its giving TLE. Please, can you have a look at my code?
Here is the code:
https://code.hackerearth.com/fc4042j?key=3bf86a65804663409e836178af8310a6
Here is the link to my latest submission for this problem
http://mirror.codeforces.com/contest/816/submission/30966480
In 815B/816D the pattern found for the
n mod 4 = 2on the fourth constant should it be(((n-2)/2) 1)?Please add link to editorial to "Contest Materials" section for the tasks. Thank you in advance!
I have some complaints.
B: 'Well, we can do something and find magic formulas but wait, we can do something different with triangles and find other magic formulas, now it is much more beautiful!' I will leave aside question about why give this problem to the round. But how can 'watch closely' be an editorial?
C: 'Rather straightforward O(n3) DP' is actually O(n2).
D: Sorry, I stop reading after words 'segment tree'. 27860187 — easy O(n + p + q + r) solution without any data structures.
E: WTF is this?! 'Now, draw the trees with root segments 40, 41, 42, ..., 47' Really? You expect me to draw all these trees to find some really strange pattern which you don't even bother to prove? Who needs proofs anyway. If you don't have any other solutions then 1. How you prove for yourself that all these patterns lead to a correct solution? 2. Why to give this problem on round? You really expect that someone will make all these great observations during two hours?
And yes, there are much simpler solutions 27862681. And (look in comments) there were problems similar to given and even this exact problem.
To sum it up: we have three problems (out of five) for which there exists a solution simpler than it was expected. And expected solution for E looks like it is really unlikely to come up with.
I think that coordinator should have done much more serious work here.
I completely don't get your point in B. I am satisfied by described solution.
For D I think there are few ways to solve this problem instantly using really standard ideas like some segment trees or I thought about some set of pairs that also does work. You came up with some tricky solution, fine, you're clever, but that doesn't mean that problem is shit. However I didn't really like it anyway because "compute volume of sum of boxes" doesn't sound like an innovative problem.
Reread editorial for B. Phrases that are closest to formal proof are 'Observe the following picture' and 'Am I the only one whose mind is on the verge of exploding?'. We observe and notice, we don't prove.
Did you notice the picture with yellow and blue numbers :|? Isn't that sufficient for you as a proof? Would you feel better if instead of that there will be some hard to follow formulas that will prove what is obvious from that picture? Observing, noticing and proving for statement of such type are typically the same thing. By no means I want to say that noticing pattern is always sufficient for a proof but here once we note pattern from picture then converting it to formal proof is a task for 10years old child, I thought you are capable of such feat.
I get your point. You can deduce the proof from that picture so you think that everybode can.
Yes, triangle on the picture is quite convincing and I can make from it a proof. But that's not what author says. He says 'It is beautiful that is why it's true'.
Maybe you are right about D. Maybe I just tried to find more examples of strange things in this round and went too far.
Can you explain your O(n + p + q + r) solution for problem D?
We will see card (x, y, z) as cube with coordinates (x, y, z). All our cards form a cuboid with sides p, q and r. Let's count the number of such cards (x, y, z) that there exists a card in our set such that (x, y, z) cannot beat it. For given card (X, Y, Z) from our set all such cards forms union of three cuboids: (y ≤ Y, z ≤ Z), (z ≤ Z, x ≤ X) and (x ≤ X, y ≤ Y). So our task is to find the volume of the union of this figures for all cards from our set.
First cuboid has 'free' x coordinate, second -- 'free' y coordinate and third -- 'free' z coordinate. Let's regroup this 3n cuboids in three groups by free coordinate. How the union of all cuboids in one group looks like? Let's look at group with free z coordinate, for example. z coordinate remains free, and union of rectangles froms ladder-like structure. For every x0 coordinate there is y(x0) such that cube with coordinates (x0, y, z) is in our figure iff y ≤ y(x0), and y(x0) is non-increasing function. There also exists non-increasing function x(y0) with similar meaning. We can build all the functions y(x), x(y), z(x), x(z), z(y) and y(z) in linear time with suffix maximums. That's arrays AB, BA etc. in my code.
Now we want to find the volume of the union of this ladders with one free coordinate. Let's use inclusion-exclusion principle. Now we want to calculate volumes of ladders, pairwise intersections of ladders and intersection of all ladders together.
Volume of one ladder is easy to calculate: it is area of planar ladder multiplied by the legnth of free coordinate. The area of ladder is just sum of y(x) for all x.
Volume of intersection of two ladders is not harder. Let's assume that these two ladders have y and z free coordinates. Let's iterate over x. Then first ladder gives us the range of z and the second gives range of y. Each cross-section with fixed x is a rectangle with sides z(x) and y(x). Sum of z(x)·y(x) over all x is the volume.
And the volume of intersection of all three ladders is the hardest part. Again, let's iterate over x. That gives us rectangle z(x) × y(x), but there is also a ladder y - z. We should intersect the ladder with the rectangle to get the cross-section for given x. There is two cases: rectangle inside the ladder and reactangle has part outside the ladder. In the latter rectangle z(y(x)) × y(x) lies inside the ladder and we should add sum of y(z) for all z(y(x)) < z ≤ z(x) to its area. To get this sum in O(1) we can use prefix sums.
Please refer to my code for further explanations. There are three clear parts each doing what is written here.
So we use prefix sum instead of segment tree here, is that correct?
So you have already Accepted the problem right before you have solved this......You didn't get the segment tree approach? 44903594
Hi, Please could you explain why your solution for problem C is O(n^2)? You have this loop in your code
First you iterate over each node, inside that you have two loops that iterate over the size of the node and the size of the father, in a line-graph (i.e. 1 — 2 — 3 — 4 — ... — n), this won't be O(n^3)?
Thanks
Let's suppose each vertex v has its own 1v and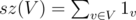 for some set of vertices V. Now calculate the number of iterations of inner cycle in my algo like this: whenever you want to add szv·szu, replace each sz with corresponding sum of 1 and then open brackets. It is easy to see that 1v·1u appears exactly once for all different v, u, so the sum is exactly n(n - 1) / 2.
for some set of vertices V. Now calculate the number of iterations of inner cycle in my algo like this: whenever you want to add szv·szu, replace each sz with corresponding sum of 1 and then open brackets. It is easy to see that 1v·1u appears exactly once for all different v, u, so the sum is exactly n(n - 1) / 2.
I tried the question DIV1 C using the same approach which you have suggested but I'm getting TLE and to me, it seems like the complexity of my code is O(n^2 * logn) and for the given constraints it should be enough but still its giving TLE. Please, can you have a look at my code? I am not able to figure out why my solution is still O(n^3).
Here is the code: https://code.hackerearth.com/fc4042j?key=3bf86a65804663409e836178af8310a6
Here is the link to my latest submission for this problem
http://mirror.codeforces.com/contest/816/submission/30966480
I think that this piece of code may be problematic:
I would say that k should go to sz[child[i-1]]. You should modify your algo, so that one loop goes to NOW and the other iterates just over the size of the child's subtree.
Hey, Thank you for your reply. I made the changes which you suggested but still its giving TLE on the same test case. Here is the link to my latest submission. Please have further look if you think we can further improve the complexity.
http://mirror.codeforces.com/contest/816/submission/31972625
Thank you, once again for helping me !!!
Another tle possibility is the fact that you increment NOW before the loop. The idea is that you should iterate over each possible number of vertices from your subtree and everything which was already processed.
I don't understand your code exactly — for some reason you update dp for children first. In order to update dp for next child you are using values for the previous child. The idea is to calculate dp for curr using the values from children. This way the loop which iterates over child subtree would go from 1 to sz[child[i-1]] and the loop for curr would go from 0 to NOW. After you process child[i-1] you add appropriate size to NOW.
In current version vertices from subtree are paired with each other, which could bump the complexity to O(n^3) as they can be paired with each other multiple times.
EDIT. To make sure that you understand the idea. Each value from the subtree can be assigned to different vertex from the subtree. You calculate values for 1,2,3,..,sz[subtree] vertices, so every time you add one new vertex. Now you want to get every vertex from the subtree and try to match it with values which are already calculated — each such value represents one of the vertices already processed, using the same logic. When you do comparison dp[curr][j+k] = min(dp[curr][j+k], dp[curr][j] + dp[child][k]) you do the matching (j-th processed vertex and k-th vertex from child's subtree). Now, you have to make sure that on every stage you match vertex k, with vertex j, such that you have never matched them before -> this way you visit O(n^2) pairs in total. Otherwise you will be matching vertices multiple times and you have n possibilities to do that. Hence your total number of matches could be O(n^3).
Thank you for your help. I got an AC finally. Because of your comment, I finally got the idea why the code was giving TLE. I made the changes you suggested and got an AC.
You're welcome!
Does anyone have a rigorous proof of Div2 D/Div1 B?
I am simply unable to understand why the last two terms come out as the answers to the "simpler" versions a1,a3,a5,... and a2,a4,a6,...
Claim: So long as the number of terms is even, in 2 lines, the each term will be dependent only on the similarly colored term.
Proof: Basically what is shown, because arbitrary numbers are being used the result will not depend on input. The addition pattern is going to be the same since the number of terms is even.
This proof shows that after 2 lines it will still be true. We can again use it to show that after 4 lines it will still be true. And so on to the last line.
"woosh"? Does this word exist? XD
It surely exists, and it's pretty rad.
https://xkcd.com/1627/
Humans :
How to solve div 2/1 A B C D E ?
How to prove div 2/1 A B C D E ?
I know simpler solution than editorial.
round winner:
Is 'woosh' a real word?
Yo mama is a presentation error.
In f(i, j) = min(f(i, j), f(i, j - k) + f(i, k)), how are we making sure that we don't repeat elements?
Waiting for another contest !!
You might know it as C(n - 1, k - 1). It's number of ways to choose k - 1 elements from n - 1 elements.
can someone explain why can we skip the largest subtree, i didn't got that point. thanks in advance
Can someone explain me why the contribution of the K-th element when there are n elements is precisely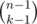
In Div2 C, what if we gave decrementing a row by 1 the weight of X and decrementing a column by 1 a weight of Y, would the problem change? will the greedy approach still be guaranteed to work? and how to optimally approach it in this case.
When n mod 4 = 2, the 4th pattern seems wrong, should be C((n - 2) / 2, 1)?