jonathanirvings's blog

2017 TopCoder Open 3B problem
By jonathanirvings, history, 7 years ago, In English

Is anyone else experiencing arena problem right now, or is it just me? I can't log in to the arena.

  • Vote: I like it
  • +130
  • Vote: I do not like it

Comments Comments (71)
| Write comment?
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by jonathanirvings (previous revision, new revision, compare).

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

same here

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Me too

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Also can't log in.

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Tagging cgy4ever

→ Reply
»
7 years ago, # |
  Vote: I like it +17 Vote: I do not like it

is it rated?

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Me too...

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

TopCoder forum is down as well.

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Same problem here. I noticed it when I tried to open a problem.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Me too. Then I noticed that there are no updates in the chat window. Then I suspected that my Internet connection is down, so I tried to open Codeforces. Then, I restarted arena. It couldn't log in.

    → Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

There goes my chance to gain ratings :(

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +23 Vote: I do not like it

    Haha, I also wonder how many points I would get by solving nothing

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      In Round 3A, I lost 6 points (2380 -> 2374) for solving nothing.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +10 Vote: I do not like it

        But you are red in topcoder, I am the lowest rated guy in the (not working) contest = P

        → Reply
»
7 years ago, # |
  Vote: I like it +5 Vote: I do not like it

I was able to read Easy, but the connection downed, and it is not working now.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +21 Vote: I do not like it

    I've managed to read Hard, and then got the same problems.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I can't login..

→ Reply
»
7 years ago, # |
  Vote: I like it +20 Vote: I do not like it

I was working on poor Internet connection.

I worried about my rating.

Found this CF article.

???

PROFIT

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

First my compile requests did timeout, then I have noticed Burunduk1 also complaining about compilation problems, then I tried to say "me too" and it was not shown, then I could not login at all, and could not access the website either.

→ Reply
»
7 years ago, # |
  Vote: I like it +25 Vote: I do not like it

I guess this is going to be unrated. Poor task authors...

→ Reply
»
7 years ago, # |
  Vote: I like it +71 Vote: I do not like it

I guess by now it definitely requires a rematch. Question is when?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Also is this safe to discuss the problems now?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I think no. There is not any official announcement from Topcoder.

      → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      I'd wait to be safe. We can speculate on rematch date though. According to rules last time I read them it is same time, next day

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +10 Vote: I do not like it

        Also according to the rules, sometimes TC admins may have to adjust things, which will be the case this time, rematch definitely won't be tomorrow. We will post more information once we have determined the best course of action.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +10 Vote: I do not like it

          It would be sad if it would be next Saturday

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            Probably isn't.... not official yet, but thinking probably two weeks from now.

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              Trying our best to make sure we have good problems to use, that weren't written by someone who is eligible to compete, etc, etc.

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                7 years ago, # ^ |
                  Vote: I like it 0 Vote: I do not like it

                The day of Warsaw event?

                → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Same here...

→ Reply
»
7 years ago, # |
  Vote: I like it +10 Vote: I do not like it

t-mac Could you officially confirm that today's round is cancelled?

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +20 Vote: I do not like it

    Confirmed. (At least, so far as official TCO advancement and ratings are concerned.)

    → Reply
»
7 years ago, # |
  Vote: I like it +15 Vote: I do not like it

I am on an airplane now. It will be lucky for me if this round is procrastinated.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I think that's a sign:))However, if you are on a plane, then how could you write here? Or it hasn't departed yet?

    → Reply
»
7 years ago, # |
  Vote: I like it +18 Vote: I do not like it

Actually I got a response from my tweet instead. Not very helpful though :(

https://twitter.com/Topcoder/status/898948295996964865

→ Reply
»
7 years ago, # |
  Vote: I like it +15 Vote: I do not like it

The arena seems to be working now.

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I can log in now. The contest is not available anymore and t-mac replied to my question what is going to happen that they are 'talking internally'.

Edit: the round just became available

→ Reply
»
7 years ago, # |
  Vote: I like it +13 Vote: I do not like it

we are working on this and figuring out the solution. thanks for your patience and stay tuned!

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +25 Vote: I do not like it

Message in the arena:

"The tournament round today won't count, but I'm leaving it up for fun/practice, unrated of course. We are determining internally how to handle a replacement round, and will notify everyone as soon as we can."

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +20 Vote: I do not like it

Official updates are coming on the TC site, and there will be e-mail notification, etc, but the replacement 3B will take place on Sept 9th.

Note that the day before is the Pittsburg regional event, and the day after is the regional Wildcard round: So, busy weekend, but will be a fun one!

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Did you mean Sep 9th, which is a Saturday?

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +21 Vote: I do not like it

    My initial plan was to go to Poland to hunt a slot for wildcard in case I fail in 3B.

    Now the decision is more difficult. Should I go to Poland to increase the probability of qualification?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +66 Vote: I do not like it

      Going from Japan to Poland to get a chance to win a trip to some onsite. OMG

      → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +28 Vote: I do not like it

      What about going to Poland simply because it is a nice place? :)

      → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +21 Vote: I do not like it

      Are you really serious or are you just making jokes ;p? Btw don't go to Warsaw event, don't destroy my hopes xD.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +15 Vote: I do not like it

        I was serious. In Japan, many teams go abroad to get slots for ICPC WF. Why don't you go abroad for TCO? But this year I won't go.

        I've been to Poland once for no reason. When I visited Berlin, I had a day off. Then I decided to take a train to Frankfurt (Oder) and go to Slubice on foot.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
          ← Rev. 2   Vote: I like it -10 Vote: I do not like it

          In Poland teams travel abroad to get ICPC slots also, but there is a difference between 6 teams travelling from Poland to e.g. Croatia with whole stay covered by university and travelling probably alone from Japan to Poland paying for whole trip from own funds in order to get a chance to get a chance to qualify to TCO. But if you want to then probably it can be fun in some way ;p.

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it +10 Vote: I do not like it

            That's different. Polish teams travel abroad because our regionals happen to be abroad that year. You travel because you have to. Japanese teams travel abroad because of the weird way ICPC works in Asia. Even though there is a Japanese regional contest, the Japanese (and also other Asian) teams may go compete in other regionals instead, possibly with different teams from the same university competing in different regionals. This can be a strategic decision.

            → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    TCO10-12 (at least) had the following rule: In the event that a round must be cancelled for any reason, the round will start the following day at the same time. I am rather unhappy that this rule no longer exists -- Sept 9th is not very good for me, while reserving the next day is usually easier :(

    What happens if someone qualifies both to the Finals and the Wildcard Round? Is the Wildcard Round spot given to the next competitor?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +20 Vote: I do not like it

      "while reserving the next day is usually easier" — huh? If you pick a day x then probability that I have no plans on day x+1 is significantly smaller than on day x+21, even when conditioned that I was able to write a contest on day x. And I thought that similar would be true for others as well.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        The problem is with going to various kinds of trips. Especially for difficult rounds such as this one, doing a round during a trip may be mostly pointless for some reason (due to bad Internet access, noises, people thinking it is fine if they are talking loudly, interrupting you, or making fun of you, having to bring your computer and keyboard with you, etc.). Trips usually take more than one day. On the other hand, local events tend to be easier to cancel or to be late for. Also, assuming that the rule exists and you know about it, you can arrange the next day to be free just in case :)

        → Reply
»
7 years ago, # |
  Vote: I like it +10 Vote: I do not like it

I know a pattern for 1000 with l ≥ 4: 1 - 0 - (b - 1) - (b - 1) - ... - (b - 1) - (b - 2) - (b - 1). Is it easy to handle for l = 2, 3?

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +10 Vote: I do not like it

    L = 2 is easy (brute force all ratios from 2 to b - 1).

    I think L = 3 is the main part.

    By the way, if you find a short solution, you can just append zeroes to get longer solutions.

    → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 4   Vote: I like it +40 Vote: I do not like it

    You can add 0 at the end of your answer. So you only need to find the shortest one.

    For L = 2, the answer should be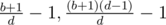 . If b ≠ 3 and b + 1 is not a prime number, The shortest answer is 2.

    For L = 3, there are 4 cases.

    pb2 + qb + r|qb2 + pb + r. pb2 + qb + r|(qb2 + pb + r) - (pb2 + qb + r) = (q - p)(b - 1)b. So you can enumerate the value of q - p and find the divisors of (q - p)b(b - 1).

    pb2 + qb + r|rb2 + qb + p. pb2 + qb + r|(r - p)(b2 - 1). It is similar to the first case.

    pb2 + qb + r|qb2 + rb + p. Let x = qb + r, y = p. k(yb2 + x) = xb + y. So x / y = (kb2 - 1) / (b - k). You only need to enumerate k, and find gcd of kb2 - 1 and b - k.

    pb2 + qb + r|rb2 + pb + q. It is similar to the third case.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +33 Vote: I do not like it

      Tip: if you remove all "*" signs then your post will be 3 times more readable. Even better, you can write qb2 instead of q * b * b If you really want to put there multiplying dot then \cdot is the thing you are looking for -> q·b·b

      → Reply
»
7 years ago, # |
  Vote: I like it +10 Vote: I do not like it

Were the constraints for 500 intentionally lowered to allow DP solutions? Max flow solution seems to be much easier to implement, however the constraints strongly suggest that the intended solution was exponential DP since max flow could work with much larger N, M or box size.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    Can you explain your flow solution?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +85 Vote: I do not like it

      If there's no valid path from upper-left to lower-right corner, there must be a "blocking path" from left/bottom to right/top, more precisely it should have the following properties:

      • Each cell in it has an obstacle.
      • For two consecutive cells max(|r1 - r2|, |c1 - c2|) ≤ 2 should hold (such that 2x2 box can't be squeezed in between two consecutive cells).
      • The path starts either in the first two columns or in the last two rows (such that 2x2 square can't be squeezed in between this cell and a wall).
      • Similarly, the path should end either in the first two rows or in the last two columns.

      So the problem becomes equivalent to "remove minimum number of obstacles such that there's no blocking path", this is the same as finding a min-cut in the graph where we split each cell into two, add edge of capacity 1 between two copies of the cell and then add edges with infinite capacity between any two cells which can be consecutive in a blocking path (and also add some edges to/from sink/source for cells in the rows/columns close to the boundaries).

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +15 Vote: I do not like it

        That's a nice solution. I've coded it up in the practice room and it passes system tests.

        → Reply
»
7 years ago, # |
  Vote: I like it +25 Vote: I do not like it

If I'm correct, both passed solutions to 500 submitted during the round utilize the fact that, at any moment, one only needs to remember the last two unblocked cells on our path.

Is there any simple proof of this?

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 6   Vote: I like it +5 Vote: I do not like it
    Completely wrong due to my faulty logic
    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +30 Vote: I do not like it

    The following is not a formal proof, but one that seems good enough for me :) Suppose that we need to remember three cells, let's name them a, b and c. Then the path must first visit a for the first time, then b for the first time, then c for the first time, then a for the second time, then b for the second time and finally c for the second time (if the path was for example abcbac then we could take a 'shortcut' between the two a's, costing at most two instead of one, but saving the cost of b). If we need to start in one corner and end in the opposite corner, then (for topological reasons) this structure (abcabc) is not possible without the path crossing itself (try it on paper), so we never need to remember three cells.

    Below are two examples. The first example shows that we do need to remember two cells and the second example shows that if the destination (or source) is not on the border, then we need to remember more cells. The second example can be extended to any number of cells that need to be remembered (if the grid can be large enough). In the examples S stands for source, D for destination and lowercase letters for initially blocked cells that need to be removed in the optimal path.

    SS..####
SS..####
##..####
....####
...a....
..#.....
.....#..
....b...
####....
####..##
####..DD
####..DD

    SS#####.......
SS#####.......
..###....###..
..###...cDD#..
..#....#.DD#..
..#...b...##..
.....#....##..
....a...####..
####....####..
####..######..
####..........
####..........
    → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +30 Vote: I do not like it

    EDIT: krijgertje was faster :)

    My explanation doesn't look formal enough, but anyway, here's my attempt.

    Usually, like Case 1, simple Dijkstra works. The cost to move the square from position p to position q is the number of cells that are covered by q but not by p.

    It fails only when things like Case 2 happens. We shouldn't count the cell A twice.

    This pattern can be nested in more complicated ways. In Case 3, we have to keep both A and B before reaching A for the second time.

    In Case 4, do we have to remember three cells? No. Instead of using A+B+C, we can use A+C+D to achieve the same cost.

    Let's call a cell "special" when the cell is visited twice. Suppose that in some case we have to remember three special cells. Call them A, B, C in the order of first visits. Then, the second visit to A must be after the first visits to B and C (otherwise we can remember B or C after we discard A). Possible cases are:

    • (1) A1 -> B1 -> C1 -> A2 -> B2 -> C2
    • (2) A1 -> B1 -> C1 -> A2 -> C2 -> B2
    • (3) A1 -> B1 -> C1 -> B2 -> A2 -> C2
    • (4) A1 -> B1 -> C1 -> B2 -> C2 -> A2
    • (5) A1 -> B1 -> C1 -> C2 -> A2 -> B2
    • (6) A1 -> B1 -> C1 -> C2 -> B2 -> A2

    In (2) to (6), we can find a "shortcut path" like Case 4. (1) never happens. As in the picture on the bottom, the square will be trapped into a closed region.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      There's a very peculiar similarity between Med and Hard: "Consider all 6 permutations of length 3. Each of them works for some reason."

      → Reply