Your given a simple task:
For given number 2 ≤ n ≤ 1018 check prime or not it is.
Limits are: 1 second TL, 16Mb ML.
And we have solution:
bool isprime(LL n){
if(n<2) return false;
for(LL i=2;i*i*i<=n;++i) if(n%i==0) return false;
for(int it=0;it<1e5;++it){
LL i = rand()%(n-1)+1;
if(__gcd(i,n)!=1) return false;
if(mpow(i,n-1,n)!=1) return false;
}
return true;
}
where rand() returns 64-bit random integer and mpow(a,b,m) is ab modulo m.
Can you challenge this solution?
How likely is it that it is gonna say that the number is a prime, when in reality it isn't?
Fails for 999999999999999989
No, it is prime number and solution returns true.
On my machine it returns false!
show me your mpow
so you have 64-bit integer multiplication overflow...
Oh, I missed it :3 mod ≤ 1018
Using
return ((__int128)n * Pow(n, p-1, m)) % m;gave right answer. :)Link
Line
if(mpow(i,n-1,n)!=1) return false;won't never be executed.Line with __gcd is very likely to be executed for Carmichael numbers, since they have small primes in their factorization.
those numbers have at least 3 primes in factorization?
if yes then ok, because of this line
for(LL i=2;i*i*i<=n;++i) if(n%i==0) return false;im fake reyna 15241579244017681=123456791^2
note that i removed mpow line
I slightly modified the code and now it performs the power test only once, still I'm quite confident that it's correct.
The only interesting case is N = pq where p, q > 1000000 are large primes. The test fails when in - 1 = 1. However, by Euler's theorem, you know i(p - 1)(q - 1) = 1, and by combining these two equations you get ip + q - 2 = 1. There are at most p + q - 2 such i and the probability that this happens is at most (p + q - 2) / (n - 1) < 0.000002.
"There are at most p + q - 2 such i"
I don't get it. Can you explain why?
UPD. I think that if q = 2p - 1 and p, q are both primes then we have only two conditions on i: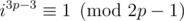
and 
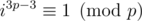. First one holds for 
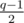remainders modulo q (exactly for quadratic residues) and second for p - 1 remainders modulo p (all non-zero remainders). So there are 
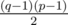solutions modulo pq (because of Chinese remainder theorem).
Let P be a polynomial of degree k (on any field). Then the number of roots of P is at most k.
(If r1, r2, ... are roots, (x - r1)(x - r2)... must be a divisor of P(x))
I still don't get it.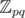
is not a field. I expressed my doubts in UPD to my previous comment.
Yes, you are right, I was stupid :)
Do you know how to challenge this solution or you wondering whether it possible? It seems to me that this code is correct and 105 iterations is way too much.
It is quite well known that either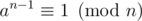
for all 
(
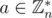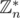is set (it is also a multiplicative group, but it is not too important)) of all remainders modulo n that are coprime to n) or it is not true for at least half of 
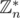elements. Lets prove that. Suppose that there is 
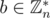such that 
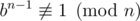. If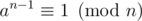 
for some 
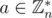then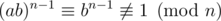 
. For different a-s ab-s are also different, so there is no more that 
such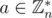 
-s that 
.
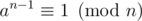(Proof is similar to proof of Solovay-Strassen primality testing)
So for numbers that are not Carmichael numbers each iteration works with probability of at least
. There are no Carmichael numbers with less than three prime divisors (it follows immediately from criterion of being a Carmichael number, see wikipedia article), so Carmichael numbers are filtered out by first loop.
answer to the question: second, i'm just interesting
Btw, it's Fermat primality test, with hack to work with Carmichael numbers.
see my answer to RomaWhite before
but thanks, i didn't knew such test, I created this function 2 years ago just for fun
Just in case someone didn't know about this. Some time ago, collares told me there were small bases of witnesses to perform Miller-Rabin deterministically for values up to 264.
Then I found this. Here you can find such witnesses and perform safely your primality test in O(logn).
You can also use the first 12 primes as candidate witnesses (source). Arguably, 12 candidates might be a bit less efficient than 7, but the set is much easier to remember.
There is a inbuilt method in JAVA in BigInteger class for prime checking. Is that method slow for prime checking? Should I avoid using that in live competition? { Method is object.isProbablePrime(int certainty))