Given an array,how to solve queries (10^5) of type Q:Value,L,R where value is a number and we need to report the count of all the numbers in the range [L,R] of the array such that gcd(Value,A[i])>1 where L<=i<=R. Given ARRAY SIZE :- 10^5 Each number 1<= A[i] <=10^5 TL = 1 Sec
→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 дней
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 дней
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 25.11.2024 06:40:58 (i1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











What are the constraints for the number of elements and the values (ai)?
I'd like to know more details (time limit, amount of numbers in array and constraints on the numbers), but anyway, I'll share the solution that came to mind.
TL = 1 sec Array size is 10^5 And Each number is 1<=A[i]<=100000
Then it should work. of the first step is OK for M ≤ 105 is OK. Now the second step has less complexity because the number of prime factors is at most 6, so it's O(Q * 26 * logN), which is also OK.
of the first step is OK for M ≤ 105 is OK. Now the second step has less complexity because the number of prime factors is at most 6, so it's O(Q * 26 * logN), which is also OK.
Do you have an online judge where I can test the solution?
This was a subproblem of some other problem (tree based) .The link to the problem is https://www.codechef.com/problems/GTREE
I think codechef problem is much easier than the one mentioned by you. Solution is similar but we can solve it without binary search just doing dfs and storing for each p how many numbers in current subtree are divisible by p.
Can you explain this " store a list of positions that divide every number"?
Maybe after the CodeChef xD
Ok.No problem.
.
can u elaborate how you are doing the binary search to obtain count of elements in [L,R] which divisible a certain mask of primes?
this problem is from codechef march long challange..
it still running dude, don't cheat
look when the blog was published :)
I think this is a problemsetter's codeforce account...
Exactly.Thank you @Dalgerok.
At first generate a list of primes that divide a number, for all number till M, the maximum number. This takes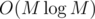 .
.
Now, for each number of the array ai, lets say the primes p1, p2, ..., pk divide that number, you can get this quickly from step 1. Go through all subsets of these primes. If a subset is pi1, pi2, ..., pir, then insert i to list pospi1·pi2... pir. This step takes O(26n).
Now when you receive a query X, take the primes p1, p2, ..., pk, that divides X, from the list generated at first. Now go through all of its subsets. Let the chosen subset be pi1, pi2, ..., pir, then count how many times a number from [l, r] appears in pospi1·pi2... pir. It can be done with two binary searches. If r is odd then add the count to answer, else subtract this count. It can be proven that this gives the answer, by inclusion-exclusion principal. Basically this counts number of numbers with at least one prime common with the query X. This step takes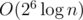
talk is cheap, send code
Which part you didn't understand?
talk is cheap, send code
Code is costly, spend time
o, really?
Ok, you can generate the list of prime divisors this way —
As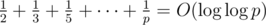 , this runs in
, this runs in 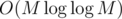 .
.
talk is cheap, send full ACed code
Why are you upvoting this post? It is cheating, and this post should be deleted immediately, I think because it violates CodeChef rules and principles of the competitive programming.
This blog post was created 6 months ago. However the current interest in this post can be attributed to CodeChef's problem.
This blog has nothing to do with CodeChef, the thing should be deleted is CodeChef problem. CodeChef should really care about problems of long challenge, because in 10 days even we can find code of problem from internet.
Sorry, I missed this fact. So it's good that later comments are downvoted and unclarified.
You also can do it with bitset. numbers less than 10^5 has less than 7 prime divisors. So for every primes less than 1e5 set the bit of positions of those numbers which are divided by.
GCD(x, a[i]) has no common prime divisors If their GCD is 1. you can travel through prime divisors and check how many numbers you can divide in the given range. then the ans might be (r-l+1- NumberofSetBit).
you can solve it easily than other technique.
Can you please explain more on this line "So for every primes less than 1e5 set the bit of positions of those numbers which are divided by." If possible, please post the link to code of this approach.