Given an int array which might contain duplicates, find the largest subset of it which form a sequence. Ex: {1,6,10,4,7,9,5} then ans is 4,5,6,7
Sorting is an obvious solution. Can this be done in O(n) time ??
Thanks in advance :)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
Given an int array which might contain duplicates, find the largest subset of it which form a sequence. Ex: {1,6,10,4,7,9,5} then ans is 4,5,6,7
Sorting is an obvious solution. Can this be done in O(n) time ??
Thanks in advance :)
| Название |
|---|



I have a simple idea, but I am not sure whether this is correct or not.
We can adopt a "hash table" to record the integers that have appeared in the set, i.e., for some integer N, if it appears in the set, then hash[N] = 1; otherwise hash[N] = 0. Then, the problem is equivalent to finding out the longest sub-sequence consisting of "1"s. If I were correct, this solution has complexity O(n). However, this approach fails if the maximum integer turns out to be too large, for instance, 109.
It's a good approach :) I have implemented it here......Solution
Your code fails on [1,2,3,5,6,7,4].
On the one hand, using a hash table, we can dfs/bfs and find connected components on the path graph (add an edge for each adjacent elements) to solve the problem in Θ(n) expected time.
On the other hand, on the algebraic decision tree model, your problem cannot be solved in O(n) time. To see this, take an instance of the set disjointness problem (A, B) and transform it to [3A1, ..., 3An, 3B1 + 1, ..., 3Bn + 1]. Because the set disjointness problem has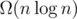 lower bound [1], your problem has the same bound.
lower bound [1], your problem has the same bound.