ryuga222's blog

Counting number triplets product equal to some x.
By ryuga222, history, 6 years ago, In English

https://www.geeksforgeeks.org/count-number-triplets-product-equal-given-number/
Can someone provide a faster solution.
Constraints : 1 <= n <= 1e5
1 <= x,A[i] <= 1e7 for all 1<= i <=n

  • Vote: I like it
  • +5
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by ryuga222 (previous revision, new revision, compare).

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by ryuga222 (previous revision, new revision, compare).

→ Reply
»
6 years ago, # |
  Vote: I like it +4 Vote: I do not like it

Hint:

Let p, q, r be elements in array A such that p*q*r==x.

p, q, r will be factors of x (including 1 & x).

1 <= x <= 1e7

Therefore, upper bound of number of factors of x is 2*square_root(1e7).

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

it can be done in O(n*factors(x)*accesstime(frequency table)) but I guess there will be much more efficient solutions.

Have three frequency tables(Maps/arrays/or other DS) for counting the frequency of a particular divisor of X. Table 1 will store number of ways to get value y(divisor of x) using just 1 number from the array. Table 2 will store number of ways to get value y using 2 numbers from the array. Table 3 will store number of ways to get value y using 3 numbers from the array.

Initially all values in the table is 0.

Now process the array from left to right(1..n) for an element a in the current position and for all possible divisors(d) of X we are going to update all the tables. if a doesn't divide d then the tables remain same else let p=d/a. Then table3[d]+=table2[p] i.e to get d using 3 divisors with one of them as a then we need to know the number of ways to form p using two divisor till the elements that we have seen previously. Similarly table2[d]+=table1[p] and table1[a]+=1.

Make sure for each element first update the table 3,then table 2 then table 1 as 3 depends on 2 which again depends on 1.

Now after processing all the elements of the array the answer is table3[X].

→ Reply
»
6 years ago, # |
← Rev. 4   Vote: I like it +6 Vote: I do not like it

Solution

We can do it in (factors(x))^2 if we keep a hashmap or any similar one. You can google and find out that there are max 400 divisors for any number less than 1e7 which makes it even pass a (factors(x))^3 solution as my (factors(x))^3 solution was passing in the contest. Let me know if you have any problem in understanding any part of the code.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    understood it. Do you have a link to the question where I can submit and try the solution??

    → Reply
»
6 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Even though this isn't appropriate for a contest, there exists a randomized solution in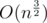 by reducing the problem to 3SUM, since .

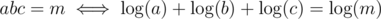→ Reply