This a problem from UAP NCPC 2016. link: problem uva-13084
In short the description is: 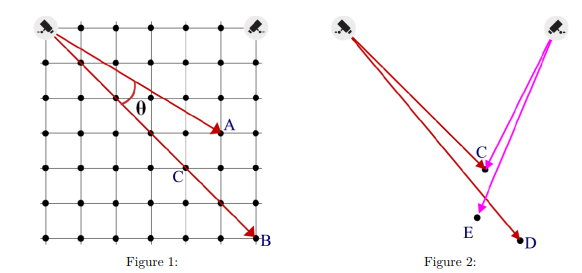
A point in a n*n grid (n is maximum 5000) is considered troublesome if there exist another point in the grid which creates angle less than atan(1/k) and it is more than 0 degree where n^2<=k<=2n^2 with respect to the upper two corners. In the above picture C is a troublesome point. Output all the troublesome points in the grid. There are at most 10 test cases. No idea How to solve this problem. Any help?











Auto comment: topic has been updated by t.muttaqueen (previous revision, new revision, compare).
Suppose the two vertices of the square is A and B. Lets call a pair of points which create an angle less than atan(1 / k) wrt A a troublesome pair.
First group all points of the square wrt their slope with A. For example — (1, 2), (2, 4), (3, 6) ..... all have the same slope and hence grouped together. Now sort the groups according to their slopes. It can be proven that a pair of points can only be troublesome if they belong to consecutive groups in the sorted list. This allows us to find all troublesome points wrt A in O(n2). Similarly, find troublesome points wrt B and take the common points.
The constraints are really bad, though. You have to do a lot of optimization to get AC.