AtCoder Grand Contest 028 will be held on Saturday (time). The writer is maroonrk. This contest counts for GP30 scores.
Contest duration: 150 minutes
The point values will be announced later.
Let's discuss problems after the contest.
→ Обратите внимание
До соревнования
Spectral::Cup 2026 Round 1 (Codeforces Round 1094, Div. 1 + Div. 2)
3 дня
Зарегистрироваться »
Spectral::Cup 2026 Round 1 (Codeforces Round 1094, Div. 1 + Div. 2)
3 дня
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | Benq | 3792 |
| 2 | VivaciousAubergine | 3647 |
| 3 | Kevin114514 | 3603 |
| 4 | jiangly | 3583 |
| 5 | turmax | 3559 |
| 6 | tourist | 3541 |
| 7 | strapple | 3515 |
| 8 | ksun48 | 3461 |
| 9 | dXqwq | 3436 |
| 10 | Otomachi_Una | 3413 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | Qingyu | 157 |
| 2 | adamant | 153 |
| 3 | Um_nik | 147 |
| 4 | Proof_by_QED | 146 |
| 5 | Dominater069 | 145 |
| 6 | errorgorn | 141 |
| 7 | cry | 139 |
| 8 | YuukiS | 135 |
| 9 | TheScrasse | 134 |
| 10 | chromate00 | 133 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2026 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.04.2026 13:01:48 (g2).
Десктопная версия, переключиться на мобильную.
При поддержке
3min
F is solvable in O(N2logN), so please try it.
My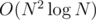
solution is slower than most of the O(N3) solutions:(
my implemention
Is there any way to distinguish them?
I have solved task A and I have read 'editorial', but could anyone explain the solution in his own words?
How to solve task B?
Basic idea is this: fix two specific elements i and j. The cost for removing block j will include the weight of i if and only if j is removed first out of the blocks in the section i through j. If not, i will be disconnected from j (or won't be present at all) by the time j is removed.
The number of permutations in which j is removed first among the blocks in i through j is N! / (j — i + 1). That's because there's N! total permutations, there are j — i + 1 blocks in that section, and by symmetry each of the blocks appears first in the same number of permutations.
By precomputing N! / k we get an O(N2) solution. It can be sped up to O(N); maybe you can see how.
Thank you very much :)
Here, two blocks x and y ( x ≤ y ) are connected when, for all z ( x ≤ z ≤ y ), Block z is still not removed. Does it mean only blocks to the left of y are connected to it ? Can someone explain the connectivity of two blocks? or all blocks which are not removed are connected ?
Connectivity is reflexive. By “x and y are connected” they mean “x and y are both connected to each other.”
Does it imply all blocks which are not removed are connected ?
No, the condition for x, y (x <= y) to be connected is that all blocks z in the interval [x, y] should not have been removed yet. If you have three blocks 1, 2, 3 and 2 is removed, then 1 and 3 are no longer connected.
Got it. Thank you !!
Can someone explain how to solve problem B ? I'm not getting it through editorial.
It seems that F1 is solvable in O(N^4/w) with bitset and some optimizations, for example this submission.
Can someone explain the solution to task B?