This problem has been taking a lot of my time lately and i would like to share it with you.

Let's first warm up with this problem:

given array v of length n and q queries (1 ≤ n, q ≤ 10⁵)

each query of the form l, r, a, x, (1 ≤ l ≤ r ≤ n), (1 ≤ a, x ≤ 10⁵)

add to the element at index l value a

add to the element at index l + 1 value a + x

add to the element at index l + 2 value a + 2 * x

add to the element at index l + y value a + y * x

add to the element at index r value a + (r - l) * x.

basically update range with arithmetic progression,apply all queries then print the final array

Now depending on the details of the problem this can be solved using prefix sums , segment tree ,or some other way

A brief explanation of the segment tree with lazy propagation solution is that in each node we store the value we want to add to the left most element in the range and the value x. When we are propagating the values we give the left child the same value for a and x while we give the right child the same value for x and a + sizeofleftchildsubtree * x for a.

If at a given node there are already values for a and x then just add the new a to the old a and the new x to the old x.

Here is a simple illustration to help you understand the approach.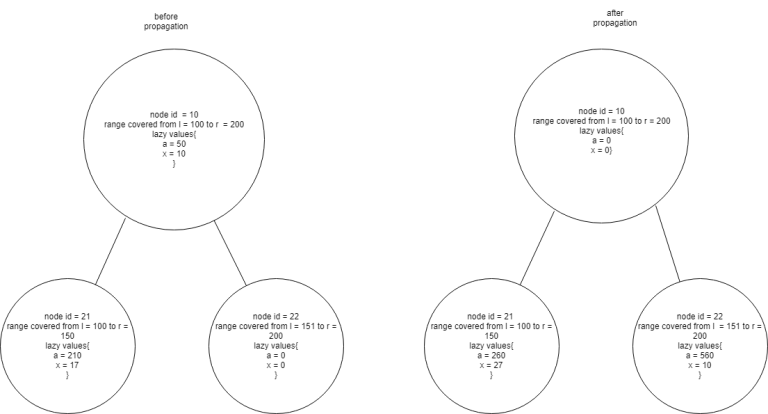

I wondered if this can be solved if a new query is introduced Max / Min range query.

P.S. we'll discuss it from Max point of view should be translated to Min easily either by multiplying everything by  - 1 or some other way.

I had many ideas but the closest i got to a thing i can call a solution is the following:

we change the array v such that it becomes the following v₀, v₁ - v₀, v₂ - v₁, v₃ - v₂, ......, v_n - v_n - 1.

Now this new array has the following property the sum up to index i equals the value at index i in the old array.

If we add the first i elements we get: v₀ + v₁ - v₀ + v₂ - v₁ + ...... + v_i - v_i - 1 as we observe everything crosses out except the last element.

This new definition enables us to update the array with arithmetic progression in a different way, instead of doing the aforementioned method we can instead add x to all indices between l + 1 and r - 1 inclusive , add a to index l ,and finally add a + (r - l) * x to index r.

To prove this we can simply look at any index between (l, r) and see how its value changes when we apply the update:

i, i + 1belongto(l, r) lets say a_i got increased by a + y * x so a_i + 1 got increased by a + (y + 1) * x

so,v_i + 1 - v_i = old(v_i + 1) + a + (y + 1) * x - (old(v_i) + a + y * x) = old(v_i + 1) + a + y * x + x - old(v_i) - a - y * x = old(v_i + 1) + old(v_i) + x

the first element in the range will have a different formula which will look like this v_{firstindexinrange} + a - v_{firstindexinrange - 1} same thing for the index after the last index in the range v_{afterlastindex} - v_lastindex - a - (r - l) * x

The range maximum now is equivalent to prefix that ends in range [l, r] with maximum sum (which i couldn't solve).

I was wondering if anybody has any idea how to make this solution work or has a different approach deterministic may it be or not.