В этой задаче нужно было посчитать количество пар подряд идущих одинаковых букв. Это можно сделать в один цикл за время O(N).
В этой задаче нужно было аккуратно реализовать процесс, описанный в условии. Нужно было t раз обменять два элемента i и i + 1 местами, если на i-ом месте стоял мальчик, а на i + 1-ом стояла девочка. Главное, не нужно было одну девочку двигать влево несколько раз за одну итерацию. Решение можно реализовать за O(N·T).
Эту задачу будем конструктивно, даже скорее используя индуктивный подход. В начальный момент у нас есть квадратная матрица размера n и n - 1 единица в ней. Следовательно, существует столбец, в котором нет ни одной единицы. Поставим этот столбец на n-ое место. Таким образом, правый нижний элемент будет равен 0. Теперь найдем любую строку, в которой есть хотя бы одна единица, и поставим ее на n-ое место.
Мы добились того, что в клетке (n, n) стоит 0, а также в последней строке стоит хотя бы одна единица. После этого можно уменьшить размерность задачи, то есть n: = n - 1. Заметим, что в этой задаче у нас будет не более n - 2 единиц, следовательно эту задачу решить аналогичным образом. Когда n окажется равным 1, алгоритм нужно завершить, поскольку в первой строке будет 0 единиц. Всего у нас получается O(N) операций swap, не более двух для каждого n.
Расскажу несколько идей решения этой задачи. Сначала предложим решение за O(N4). Переберем ребро (u, v) длины len, на котором окажется точка из ответа. Пусть эта точка находится на этом ребре на расстоянии x от вершины u. Тогда расстояние до любой другой вершины i равно min(x + d[u][i], len–x + d[v][i]), где d[x][y] — расстояние между вершинами x и y. Приравняем эти величины, посчитаем критическое значение величины x для вершины i, получим x = (len + d[v][i]–d[u][i]) / 2. Отсюда видно, что ответ на задачу полуцелый. Таким образом, для каждого ребра и для каждой вершины получим набор таких критических точек. Проверим каждую из них помимо самих вершин графа (границы отрезка). Возможно такое решение вполне реально сдать, добавив какие-нибудь оптимизации или идеи.
Также можно было решать задачу за O(N3·log2). Умножим веса всех ребер на 2. Теперь переберем ребро, на котором находится ответ и сделаем бинарный поиск по ответу (уже в целых числах). Чтобы проверить текущий ответ, нужно перебрать вершину i, считая что ответ достигается в этой вершине. Тогда получим, что точка на этом ребра должна лежать либо <= какого-то l[i], либо >= какого-либо r[i]. Эта подзадача решается в оффлайне с помощью сортировки событий и поддержания баланса.
Также можно было попытаться сдать тернарный поиск на каждом из ребер графа. Однако, поскольку в чистом виде он работает неправильно, нужно было разбить ребро на некоторое количество отрезков и искать на каждом из них.
Последние два решения проходили, если их аккуратно реализовать. Еще отмечу, что также есть решение за время O(N3) автора задачи RAD.
266E - Опять запросы к массиву...
Эта задача решается с помощью структуры данных. Будем использовать дерево отрезков, причем будем поддерживать k деревьев отрезков для каждой из степеней. В вершине будем поддерживать взвешенную сумму с соответствующей степенью, а также число, которое означает цвет всего отрезка, если такой есть.
Пользователь Egor в комментариях к посту, а также пользователь mexmans в комментариях к разбору, описывали свои формулы для получения ответа. Постараюсь объяснить как их можно получить. Во-первых нужно выписать, что умеет в качестве запроса считать ваше дерево отрезков. Оно умеет получать сумму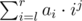 
. Вам же нужно посчитать 
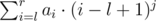, можно записать как 
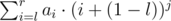. Теперь нужно расписать на листочке последнюю сумму для первых степеней, хотя бы до трех, и отнять из первой суммы (ответ на запрос дерева) вторую (то что нужно получить). Получится выражение, которое нужно вычесть из числа запроса для получения ответа на задачу. Это просто бином Ньютона без старшей степени.
Таким образом, ответ для степени j выражается как разность числа запроса и бинома Ньютона со всеми степенями, которые меньше j (эти значения также можно запрашивать вашим деревом отрезков). Частичные суммы степеней и сочетания нужно заранее предпосчитать. Решение имеет сложность O(N·K·log(N)).
tutorials for d & e?
Bit patience my friend :)
It has not been ready yet.
А истина была где-то рядом)
Очень понравилось решение С. Просто и понятно.
For D i tried the following approach but somehow couldn't finish debugging it.
Will it work ?
А ведь можно разборы и заранее писать!
Кто-нибудь может ответить мне, прокатит ли такое решение задачи D :
Общая сложность выходит порядка n^4*log(n), однако из-за моей корявой реализации, программа получает ТЛЕ, поэтому просто хочется узнать, работает ли алгоритм
Upd. Спасибо, понял, почему ТЛЕ , однако вопрос, правильный ли алгоритм, остается..
Ну дейкстра вообще — то работает на O (M logN), что в худшем случае O (N^2 logN), так что асимптотика будет O (N^4 log N) + еще и константа set, еще и pair, каждый раз создавать новый set <pair <int, int> >, еще и функции возвращать вектор... Понятное дело, TLE :D
Спасибо, исправил, действительно O( NlogN + MlogN )
Не знаю корректно оно или нет, но т.к. асимптотика Дейкстры — O(mlogn), а тут не исключён случай полного графа, напишите простую дейскстру за O(N^2), возможно пройдёт.
In problem C the important part is how can you find the 0 row fast (I mean the row with all numbers 0 in it), because you do it O(N) times and naive way (O(N^2)) is not sufficient. I used some dynamic arrays and updated them after each swap. For me the difficulty was in implementation and not in the algorithm, I got it in about 5 minutes.
n = 1000 whats the problem with n^2 algo?
you do N^2 thing O(N) times, in total it becomes O(N^3). I mean in O(N) times you will have to find 0 row in remaining square. That's not a straightforward thing to do, for me it was harder than the part that is written in the tutorial.
the two steps are independent, so this gives O(n^2), which is feasible. you just need an array of size n counting the number of ones in each column to search for the appropriate column in O(n)
that's what I did actually
D and E ? at least some hint ?
E: 1) Let's understand how to solve this problem if k for all queries to calculate the sum is equal to 0. It's quite easy to do it: we can just use a segment tree.
2) Let's learn to answer queries where k is greater than zero. Let's assume that we know a correct answer for a node's left child and right child. We need to merge node's children answers. To do it, we can figure out the following formula: answer for current node and power k ans[k] = ans_left[k] + ans_right[k] + sum for all 1 <= j <= k ans_right[k — j] * L ^ j * c[k][j], where ans_left and ans_right are the answers for node's children, c[k][j] is a binomial coefficient and L is the length of a segment represented by the left child of the node.
3) However, we still don't know how to process assign queries. But this is rather simple: if we precalculate prefix sums for all powers, we'll be able to find a value for a certain node in a tree in constant time even if its value has been updated.
Such solutuion works in O(N + M log N) time.
thanks for the hint
It seems that I had underestimated the C problem — very interesting idea to solve it.
Thanks for tutorial!
Could I solve D Problem, using Hakimi algo, for searching an absolute center of Graph?
Article in Russian is here:
http://www.uchimatchast.ru/teory/abs_center.php
(algo in the bottom of the page)
For problem C there is an O(n) solution. 2997252 (this is not my original idea, i learnt it from 2993213 and edit the swap part to make it O(n)) The main idea is that after j steps, for all 1<k<=j, kth marked cell will lies in column 1 to k, row c+1(c=its column number) to j+1.
a
You are right that two swaps are needed, but by definition of Big-O notation, there is no difference between O(N) and O(2*N). O(N) means there is some fixed constant M such that algorithm works in time M*N for each input of any size N.
a
but it doesnt mean ,your swaps take o(2*n) ......
a
Tutorial for chinese version chick here
My idea for problem D is using ford-bellman, then with every edge[i], I find the furthest way from edge[i].x, from edge[i].y without pass through the edge[i] and determine the point, but I get WA. Anyone can explain, or have a wrong test case for that ? Thank you for helping, and sorry for my poor english :).
open your submission, you'll find the test cases below your code, and you'll find the one that gives your WA.
I know about that, but that one is too big.
How do you determinate the point on edge? You can't use ternary search, because function on it isn't convex
point = ( furthest(edge[i].x) — furthest(edge[i].y) + edge[i].w )/2; Is it right ?
No, it isn't. I thought so too, but Egor said me, that function on the edge is piece-wise linear. So you must disintegrate it on the segments. I'm still thinking, how to do it
there is a Monotonicity when the answer(ans) is increasing , you will find more such points that satisfy the condition Max_shortest_distance <= ans,so i think you can try binary search of this problem .
Have you passed the solution? If yes, please write the idea :)
До сих пор нет двух последних задач?
Still waiting for D and E solutions...
:-w
I think you should provide the link to the best solution for each problem in contest with each problem explanation [best : Good and nice implementation and complexity wise]
I think you also should provide the link to good code for each problem in contest with each problems explanation in tutorial. [ Best : Good and nice implementation and better complexity]
tutorials for D & E pls!
You can find editorial for D from problem C at here.
Hope someone can do some explanation on E!
thanks, nice explanation of problem D
Sorry but I don't think so: In the discussion of D we read: " It follows that the answer to the problem is half-integer. So, for every edge and every other vertex we get set of critical points. We should check them all include the vertices of the graph (ends of the segments). This solution may probably pass with some optimizations." I don't think that it is true for the 3-rd example. Even if not so, the proof is quite ambiguous.
whats that?
there are only solutions. where to read problems ?
a
Great source for learning the Min. Diameter Spanning Tree but the link seems to be broken. Here's the web archive link for the pdf: Link
В ожидании чуда...
в ожидании чуDE...
Может кто нибудь другой напишет разбор D, E? А то эти задачи решили 80, 40 человек.
под "кто нибудь другой" я подразумевал кого нибудь из тех, кто их уже решил...
E. Эту задачу можно решить с помощью дерева отрезков. Для каждой вершины будем хранить сумму на том под отрезке, который он контролирует сумму a[i] * (i — l + 1) ^ k для всех 0 <= k <= 5. Теперь как построить, и как пересчитывать эти значения при изменениях. Если мы знаем ответ для левого, и правого подотрезка, то задача сводится к тому, чтобы посчитать следующую сумму a[i] * (v + i — l + 1) ^ k, так как левая часть входит в сумму без изменений, а для всех правых нужно добавить кол-во элементов в левом подотрезке в сумму, которая возводится в степень. Распишем эту сумму, у нас выходит что-то вроде a[i] * (v + x) ^ k, где x = i — l + 1. a[i] * C[k][k] * v ^ k + a[i] * C[k][k — 1] * v ^ (k — 1) * x + a[i] * С[k][k — 2] * v ^ (k — 2) x ^ 2 ... + a[i] * C[k][0] * x ^ k. x ^ k для всех k можно посчитать заранее. А суммы вида a[i] * x ^ k для правого поддерева уже подсчитаны.
Коммент старый, но всё же, что такое v?
Here is my approach that gets WA.. but i don't know why..
First i compute the shortest distance between pairs using floyd warshal, then iterate all pairs getting the furthest node to each one of them.. then using binary search i get the optimal place on the road of those pair.. getting the min for every pair and printing it.
Can anybody tell me whats the problem of my solution?
Еще отмечу, что также есть решение...Ну пипец ты отметил, прям не могу, отметка года. Нам теперь этого решения месяц ждать?
Решения, которые проходят вам уже изложили. Практически всегда существуют решения, более оптимальные чем те, что указаны в разборах, об этом просто не упоминают. Автор же упомянул, попробуйте поискать списке его отосланных решений. P.S. Плюсовать такой коммент позор !
Если я правильно понял решение D за O(n^4), то оно не проходит 3-й сэмпл из условия. Кажется, нужно перебирать ребро и две вершины.
The tags for Div2B include Max flow. Can anyone elaborate on how to model this problem as a graph?
Code For B: Balance Q