sneaking's blog

Need Help In Dynamic CHT Implementation
By sneaking, history, 6 years ago, In English

I have learned the normal version of CHT quite long ago. But I am having trouble implementing the dynamic version of it. I searched for some implementations and found this. Though its pretty short, I can't understand it much :( and I will be participating in my country's OI competition soon. There I can't bring templates with me. So, if anyone can provide me with an easier code, it will be really helpful. :)

  • Vote: I like it
  • +8
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it +11 Vote: I do not like it

I found LiChao Tree easier to understand/implement, this is a good explanation

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yeah, I've read it and it is quite easy.

    But LiChao Tree can take per insert/query where L and R are the min and max possible values of x (assuming its done online). Whereas, Dynamic CHT takes 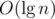. Did you ever run into problems because of this?

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      It worked just as fast as the solution with sets on the problems I tried.

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +11 Vote: I do not like it

      You won't fall in trouble due to this much change in the complexity. However this has its own advantage. You can have a line added to a segment and not the whole segment. This can be done in O(lg(R-L)), whereas in DCHT, it takes O(nlog^2n) [by maintaing a segment tree of DCHT nodes]. and its more intuitive to implement too.

      → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    But what about real number queries?

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      Generally questions are for integers. However if you need you can extend the LiChao segment tree for fixed precision too.

      Initially, the tree height was log(R-L) to make the last level range of the form i-(i+1). If you want you can build the tree to x levels getting precision of (R-L)/2^x.

      Implementation would be similar to Implicit segment tree,

      → Reply
»
5 years ago, # |
← Rev. 3   Vote: I like it +10 Vote: I do not like it

I use this code written by niklasb. Note my comment in link, the original code has a bug.

// Keeps upper hull for maximums. 
// add lines with -m and -b and return -ans to 
// make this code working for minimums. 
// source: http://mirror.codeforces.com/blog/entry/11155?#comment-162462
int inf = 2e18;
struct Line {
    int m, b;
    mutable function<const Line*()> succ;
    bool operator<(const Line& rhs) const {
        if (rhs.b != inf) return m < rhs.m;
        const Line* s = succ();
        if (!s) return 0;
        int x = rhs.m;
        return b - s->b < (s->m - m) * x;
    }
};
struct CHT : public multiset<Line> { 
    bool bad(iterator y) {
        auto z = next(y);
        if (y == begin()) {
            if (z == end()) return 0;
            return y->m == z->m && y->b <= z->b;
        }
        auto x = prev(y);
        if (z == end()) return y->m == x->m && y->b <= x->b;
        return 1.0 * (x->b - y->b)*(z->m - y->m) >= 1.0 * (y->b - z->b)*(y->m - x->m);
    }
    void insertLine(int m, int b) {
        auto y = insert({ m, b});
        if (bad(y)) { erase(y); return; }
        while (next(y) != end() && bad(next(y))) erase(next(y));
        y->succ = [=] { return next(y) == end() ? 0 : &*next(y); };
        while (y != begin() && bad(prev(y))) erase(prev(y));
        if(y != begin()) prev(y)->succ = [=] { return &*y; };
    }
    int eval(int x) {
        auto l = *lower_bound((Line) { x, inf});
        return l.m * x + l.b;
    }
};
→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    we have used this code for years and never had any problems... can you give an example where niklas original code fails?

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
      ← Rev. 2   Vote: I like it +10 Vote: I do not like it

      Yes, I found the problem while solving 91E - Igloo Skyscraper (I've built a segment tree of CHT's). When I relied on the original code the first input example wasn't correct. This is the WA solution 59667839. This is the submission with my fix that got Accepted 59662177. These solutions are identical except the changes in the "insertLine" function. (The code is a bit different for the purpose of the question)

      If you are sure the code is right maybe I had the problem while using it. If that is the case I don't understand why the problem I mentioned doesn't happen.

      → Reply
»
5 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Write a sqrt decomp version. Keep a buffer of lines, apart from the CHT structure.. When new line is given, add to buffer. and when buffer size exceeds some B, remake the whole CHT structure. During query, query on the CHT structure as well as evaluate all lines in the buffer. Set B= sqrt(n). This works almost as fast as the set implementation, and is very easy to code imo.

→ Reply
  • »
    »
    5 years ago, # ^ |
    ← Rev. 2   Vote: I like it +8 Vote: I do not like it

    ig this is pretty slow when n is slightly large. Can you ac this with sqrt decomp?

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Set has a huge constant factor, whereas sqrt method has few cache misses. Thats why they dont have too much of a time difference, as you would expect from sqrt vs log in normal probs.

      In the prob you gave, the sqrt decomp method only passes about half the test cases though. (Maybe it can be optimised more ? :P )

      → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I do not have much knowledge about cache misses (or catches?) but I think, even if you set buffer size $$$c\sqrt{n}$$$ for some constant $$$c > 1$$$, still building up a whole cht $$$\frac{\sqrt{n}}{c}$$$ times which screws us with sufficient amount of constant factors (even if you don't need to sort, there is nothing that cache memory can do by catching those caches, because you are not doing anything 'same' everytime, right?) is quite much.

        → Reply