Opencup — GP of South Caucasus: Обсуждение задач

→ Обратите внимание

До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
38:35:53
Зарегистрироваться »

*есть доп. регистрация

→ Лидеры (рейтинг)

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

Страны | Города | Организации

Всё →

→ Лидеры (вклад)

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Всё →

→ Найти пользователя

→ Прямой эфир

Детальнее →

Блог пользователя ilyakor

Opencup — GP of South Caucasus: Обсуждение задач

Автор ilyakor, 11 лет назад, По-русски

Предлагаю обсуждать здесь задачи прошедшего Гран-При.

Как решать D? Неужели все кодили эти жуткие шизофренические алгоритмы с экспонентой меньше 2^k?

Как решать G? Глядя на то, как её сдавали на первом часу, кажется, что мы совсем отупели :(

opencup

ilyakor
11 лет назад
44

Комментарии (44)

Написать комментарий?

I_love_natalia

11 лет назад, # |

+10

G: если ребра a > b нет, то ответ — кратчайший путь в графе, где веса ребер — стоимость перевозки потока. Если есть, то можно перебрать проходящий через него поток, точки, где нити потока расходятся и сходятся.

→ Ответить

ilyakor

11 лет назад, # ^ |

Хм, что за "точки, где нити потока расходятся и сходятся"? Оно что, всегда имеет вид "путь1, путь2", возможно имеющие общий префикс и суффикс? Если так — то это не интересно... Я-то думал, что тут что-то крутое есть.

→ Ответить

I_love_natalia

11 лет назад, # ^ |

+10

Да, вид всегда не более двух путей, легко доказывается перекидыванием потока

→ Ответить

pva701

11 лет назад, # |

как решать I и J?

→ Ответить

ilyakor

11 лет назад, # ^ |

I — написать persistent дерево интервалов. J — выкинуть все дуги, не лежащие на циклах, + из каждой компоненты сильной связности размера n выкинуть n - 1 дугу. Строго доказывать не умею, проверить сабмитом оказалось проще.

→ Ответить

Edvard

11 лет назад, # ^ |

Ну в I нужно очень аккуратно так, чтобы не создавалось ни одной лишней вершины. У нас решение на макстесте съедало 264 mb.

→ Ответить

witua

11 лет назад, # ^ |

← Rev. 2 →

+44

А можно сделать за O(M) памяти и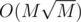 $\text{[math]}$ времени:

Отсортируем все запросы первого типа по значениям. Далее будем идти по ним блоками по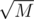 $\text{[math]}$ и строить для текущего блока массив частичных сумм, после чего для любого отрезка можно узнать количество чисел, которые были доданы на нем в этом блоке за O(1). Когда для какого-то запроса второго типа видно, что ответ в этом блоке — ищем его отдельно (полным проходом по блоку).

→ Ответить

savinov

11 лет назад, # ^ |

По J: Название четкое "Restoring the tree", а решать можно так: забьем на ориентацию ребер, тогда ответ это ans = m - n + comp, где comp — число компонент связности в этом графе.

→ Ответить

yeputons

11 лет назад, # ^ |

А можешь код I показать? У нас был TL, что-то пооптимизили с 2.6 до 2.3 локально, получили ОК.

Решение такое: сжали все координаты. Отсортировали добавления по значениям. Делаем персистентное дерево отрезков, которое хранит количество чисел <= текущего значения в таком-то массиве. Пробежались по добавлениям, теперь можем узнать количество чисел <= данного на любом отрезке массивов за логарифм. На запрос отвечаем при помощи бинпоиска.

Еще был придуман оптимайз с $\text{[math]}$ памяти до линии по мотивам одной задачи с Варшавского контеста: выполняем все бинпоиски параллельно. Тогда у нас есть Q запросов, их можно отсортировать и обычным деревом отрезков с двумя указателями выполнить одновременно с добавлениями. Итого $\text{[math]}$ итераций, каждая за $\text{[math]}$ , но линейная память.

→ Ответить

ilyakor

11 лет назад, # ^ |

Код (писал Jacob).

→ Ответить

Petr

11 лет назад, # ^ |

+21

Хорошо вам. У нас на Java зашло (в дорешивании) только после того, как мы переписали на http://petr-mitrichev.blogspot.ru/2013/05/fenwick-tree-range-updates.html . На контесте пихали-пихали, но не упихали.

Впрочем, pashka потом придумал, как делать за O(nlogn). Остаётся надеяться, что это и было авторским решением, а С++-шники случайно просочились :)

→ Ответить

cerealguy

11 лет назад, # ^ |

+13

Такой Фенвик должен быть в каждом CHelper-e.

Используя его или дерево отрезков с таким же трюком, можно поддерживать такие же операции на многомерном массиве.

А еще можно реализовать это же, избавившись от операции вычитания, и тогда можно поддерживать и запросы, где вместо + и +=, например, min и <?=

→ Ответить

Edvard

11 лет назад, # ^ |

А как это обобщается на <?= ?

→ Ответить

Edvard

11 лет назад, # ^ |

Ни фига себе. Вот это по-настоящему круто!!!

→ Ответить

kormyshov

11 лет назад, # ^ |

Если я правильно понял, то подобная модификация дерева Фенвика три месяца назад была на Хабре: http://habrahabr.ru/post/170933/

→ Ответить

oversolver

11 лет назад, # ^ |

-8

Да, но ты не Петя :(...

→ Ответить

Shapo

11 лет назад, # ^ |

J: Есть M неизвестных — величины потока, протекающего по каждому ребру. Для каждой вершины составляем уравнение того, что величина потока, входящего в эту вершину, равна величине потока, исходящего из этой вершины. Получаем матрицу N*M, находим ее ранг r, ответ ans = (M — (N — r)).

→ Ответить

ilyakor

11 лет назад, # ^ |

Неужели это заходит? Гаусс на матрице 3000x500, мало того что не ТЛится, так ещё и с точностью всё хорошо?

→ Ответить

Shapo

11 лет назад, # ^ |

0) Матрица скорее 500*3000 1) Изначально в матрице 6000 ненулевых ячеек 2) Изначально в матрице в ячейке либо 0, либо +1/-1 (входящее/исходящее ребро) 3) Все делалось в целых числах.

→ Ответить

ilyakor

11 лет назад, # ^ |

Хмм, так это всё ведь только изначально. "Всё делалось в целых числах" — это ещё удивительнее; как же оно смогло не переполниться?

Видимо, Гаусс на такой специфичной матрице делает что-то разумное, вроде dfs'а; однако априори — совсем непонятно, с чего ему работать.

→ Ответить

good_mood

11 лет назад, # ^ |

Там интересная штука выполняется, что в любой момент времени в любой колонке либо все 0, либо один раз +1, либо встречается +1 и -1 по одному разу. Поэтому на деле на каждой итерации Гаусса выполнится только одно вычитание строчки:)

→ Ответить

JKeeJ1e30

11 лет назад, # ^ |

← Rev. 3 →

J: докажем, что ответ на задачу m — n + количество компонент сильной связности, иначе говоря в каждой компоненте сильной связности можно оставить какое-нибудь остовное дерево и для него мы можем не знать велечины потока, по этим ребрам протекающие, а величину потока по всем остальным ребрам мы знать обязаны.

Необходимость(то что более чем n-1 оставлять мы не имеем право): Пусть в какой-либо КСС мы оставили n и более ребер — тогда образуется либо цикл, либо для какой-либо пары v1, v2 два пути из v1 в v2. По циклу мы можем пустить произвольный поток(и мы этот поток не вычислим), и по двум путям аналогично. Необходимость доказана.

Достаточность(то что оставить остовное дерево можно): докажем по индукции. Раз у наc дерево -> есть лист -> одно ребро, а так же известна величина потока в эту вершину, следовательно можно узнать поток по ребру. Удалим эту вершину и это ребро(мы определили поток по ним) и сведем эту задачу к меньшей.

Итого весь алгоритм решения: считаем количество КСС и выводим ответ на задачу:)

→ Ответить

Edvard

11 лет назад, # |

-10

Мы в D сдали за φ^k. Пишется очень быстро мы на обсуждение и писание потратили минут 15. Вообще эта задача уже раза 3 была. Сначала на РОИ, потом вроде на SNWS этой зимой, недавно была на СРМе и по-моему еще где-то.

→ Ответить

qwerty787788

11 лет назад, # ^ |

А можешь код показать?

→ Ответить

Edvard

11 лет назад, # ^ |

← Rev. 2 →

-13

Вот ссыль. Правда там есть отсек по времени)) Чтобы решение стало полностью правильным и честным надо каждый раз пересчитывать степень вершины согласно тому какие ее соседи уже взяты в ответ и среди таких выбирать вершину с наибольшей степенью.

Upd: код совсем ужасен потому, что мы начали ее писать за 18 минут до конца.

→ Ответить

qwerty787788

11 лет назад, # ^ |

А этот код не работает, например, на цепочке из 65 вершин :(

→ Ответить

Edvard

11 лет назад, # ^ |

← Rev. 2 →

Ну я же написал как его сделать правильным. Я знаю что код неправильный. Там баг в Ифе который сравнивает количество соседних. Надо честное количество считать.

→ Ответить

ilyakor

11 лет назад, # ^ |

А можно подробнее про φ^k? Ссылку на статью, или, если это сугубо олимпиадное знание, хотя бы доказательство?

→ Ответить

VArtem

11 лет назад, # ^ |

РОИ 2010, задача 2

→ Ответить

PavelKunyavskiy

11 лет назад, # ^ |

Общая идея такая. Будем брать вершину большой степени. Мы должны взять или ее или всех ее соседей. Если вершина степени один, то один из вариантов не нужен Итого получаем рекуретность F_n = F_n - 1 + F_n - 2. Которая решается угадай как.

Если действовать чуть аккуратнее, то можно отдельно разобрать случай, когда остались только циклы. Тогда будет F_n = F_n - 1 + F_n - 3, которая решается как примерно 1.46ⁿ.

Мне Burunduk1 как-то рассказывал про то, как похожими идеями можно искать максимальную клику за 1.21ⁿ или что-то подобное. Кажется там надо разбирать отдельно степени до 6.

→ Ответить

ilyaraz

11 лет назад, # ^ |

Вот отличный пример подобной деятельности.

→ Ответить

k0st1a

11 лет назад, # |

← Rev. 2 →

-12

как можно поучаствовать в контесте ? есть ли там дорешивание что бы потренероваться ?

→ Ответить

helThazar

11 лет назад, # |

В чем подвох в А? Упорно получаю WA 19.

→ Ответить

HAPKOMAH

11 лет назад, # ^ |

Вот тест:

3 3
4
1 >= 1
1 <= 2
2 >= 3
2 <= 4
4
2 >= 1
2 <= 2
3 >= 3
3 <= 4
4
1 >= 3
1 <= 4
3 >= 1
3 <= 2

→ Ответить

helThazar

11 лет назад, # ^ |

Ответ должен быть Yes?

→ Ответить

HAPKOMAH

11 лет назад, # ^ |

Нет:)

→ Ответить

helThazar

11 лет назад, # ^ |

Да, точно, спасибо!

→ Ответить

HAPKOMAH

11 лет назад, # ^ |

Вот мое решение: http://ideone.com/4wMFYP

→ Ответить

I_love_natalia

11 лет назад, # |

Кстати, все в F писали FFT? У кого сколько реализация работает? (у меня была 2048*2048 за 750мс локально)

→ Ответить

Edvard

11 лет назад, # ^ |

Расскажешь решение?

→ Ответить

Egor

11 лет назад, # ^ |

Эм. Перемножить ффт таблицу с перевернутой? (ну, выписать таблицу в ряд, между рядами вставить по n нулей). Потом просто для каждого вектора мы знаем, сколько таких векторов с концами в точках есть

→ Ответить