Заметим, что в данной задаче необязательно реализовывать длинную арифметику. Так как все операции за исключением умножения на 10 из-за "?" можно выполнять с помощью стандартной арифметики. А для умножения на 10 можно просто вывести в ответ нужное количество нулей.

Задача "Урок физкультуры"

Заметим, что понятие порядка мячей соответствует перестановке, а ограничение на число бросков для ученика соответствует ограничению на число транспозиций. Нужно посчитать число “подходящих” перестановок. Заметим, что если перестановку разбить на циклы, и в каждом цикле будет не более двух элементов с максимальным числом инверсий равным 1, то рассматриваемая перестановка является “подходящей”. Таким образом, задачу можно решить с помощью динамического программирования. Нужно вычислять функцию f(a, b), где a – число 1, а b – число 2, которые мы использовали. f(a, b) – число “подходящих” перестановок. Заметим, что данную функцию можно вычислять с помощью следующей формулы: 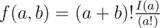, где I(n) = I(n - 1) + (n - 1) * I(n - 2)) Ее доказательство оставляем читателям в качестве упражнения.

Задача "Солнышки и лучики"

Данная задача имеет множество решений. Рассмотри одно из них. Обозначим исходное изображение за T. Будем применять к T две операции: эрозия и дилатация. Операция эрозии – замена всех пикселей, которые относятся к изображению и граничат с пикселями фона, на пиксели фона. Дилатация – это в некотором смысле обратная операция, мы заменяем пиксели фона, которые граничат с пикселями изображения, на пиксели изображения. Заметим, что для определения соседних пикселей лучше использовать 4-связность. Итак, мы применяем к исходному изображению несколько операций эрозии. После этого лучи исчезнут и останутся только центры солнышек. Далее применяем несколько операций дилатации. Заметим, что число операций дилатации должно быть больше, чем операций эрозии. Обозначим полученное изображение за P. Далее рассматриваем исходное изображение T и выделяем в нем компоненты связности, соответствующие солнышкам. Далее из каждой такой компоненты необходимо выделить части, соответствующие лучикам. Лучикам соответствуют, в свою очередь, Пиксели изображения, которые есть на изображении T, и которых нет на изображении $P.

Задача "ЭКГ"

Первое, что нужно сделать в данной задаче – это выделить цепочки в заданной очереди. Цепочка – это последовательность бобров, которые стоят в очереди непосредственно друг за другом. Таким образом, мы получим все длины цепочек и цепочку с Умным Бобром. И далее требуется просто применить стандартное ДП для вычисления возможных сумм.

Задача "Уборка"

Перейдем от исходной матрицы к двухдольному графу. Элементы матрицы (i, j) с четными значениями i + j поместим в одну долю, а с нечетными — в другую. Ребра будут соответствовать квадратам, которые находятся рядом. Далее добавим веса для ребер. Ребра, соединяющие одинаковые элементы матрицы, будут иметь вес 0, соединяющие разные — вес 1. После этого в полученном графе нужно будет найти максимальное паросочетание минимального веса. Его вес будет ответом к задаче. Обоснование вышеизложенного заключается в том, что любой ответ для задачи будет представлять собой некоторое разбиение исходной матрицы на пары. Заметим, что для некоторого разбиения минимальное число элементов матрицы, которые изменятся, будет соответствовать числу пар, в которых числа различаются. Таким образом, оптимальным будет то разбиение на пары, в котором число пар одинаковых элементов будет максимальным. Заметим также, что для построения максимального потока минимальной стоимости требовалось использовать какой-нибудь эффективный алгоритм. Например, можно было использовать алгоритм Дейкстры с кучей вместе с преобразованием весов ребер алгоритма Джонсона.

Задача "Задание на лето"

Для решения данной задачи будем использовать дерево отрезков. Рассмотрим некоторый отрезок [l;r] на этом дереве. Для него введем функцию S(x), где x – целое число. S(x) = F₀ + xA_l + F1 + xA_l + 1 + … + F_r - l + xA_r, где F_i – i-е число Фибоначчи, A_i – рассматриваемый массив целых чисел. Заметим, что S(x), для x = 0, 1, 2…, представляет собой некий аналог чисел Фибоначчи. То есть S(x) = S(x - 1) + S(x - 2), для x≥2. Из этого следует, что нам для каждого отрезка [l;r] нужно хранить только S(0) и S(1). А для вычисления S(x) для x≥2можно пользоваться следующей формулой: S(x) = S(0)F_x - 2 + S(1) * F_x - 1. Итого, разрешение запросов 2-го типа сводится к вычислению не более чем 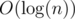значений S(x) для различных отрезков. Модификации 1-го типа выполняются тривиальным проходом по дереву. Для запросов 3-го типа нужно использовать дополнительную информацию в дереве и частичные суммы чисел Фибоначчи.

Задача "Хорошие подстроки"

Для начала нужно научиться быстро сравнивать две любые подстроки, которые можно взять из исходной строки или из одной из строк, соответствующей правилам. Это можно сделать, например, с помощью построения суффиксного массива, содержащего все строки ввода. После построения такого массива и вычисления значений LCP задача сравнения двух подстрок сводится к вычислению числа одинаковых символов и сравнении символов, которые идут после одинаковых блоков. Вычисление числа одинаковых символов эквивалентно задаче вычисления минимума на интервале массива значений LCP. Так как массив LCP не меняется, то эффективное разрешение таких запросов можно делать с помощью RMQ-алгоритмов. Таким образом, мы можем за O(1) сравнивать две любые подстроки. Заметим, что время препроцесса зависит от используемых алгоритмов для построения суффиксного массива и построения RMQ.

Далее нам нужно научиться находить число вхождений некоторой подстроки исходной строки в строку одного из правил. Это можно делать с помощью бинарного поиска по суффиксному массиву строки правила. Заметим, что мы можем сравнивать две подстроки за время O(1). Поэтому сложность поиска числа вхождений подстроки в строку будет 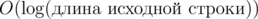. Теперь рассмотрим некоторый суффикс исходной строки. Мы знаем его LCP с предыдущим суффиксом. Это будет нижняя граница на длину этого суффикса. Заметим, что число вхождений некоторого префикса рассматриваемого суффикса монотонно зависит от длины этого префикса. Поэтому, для каждого правила можно бинарным поиском определить, какой может быть минимальная и максимальная длина префикса, чтобы он подходил под правило. После чего необходимо просто пересечь все полученные интервалы.

Возможно, что с использованием других структур данных на строках можно получить более простое решение. Техническая реализация рассматриваемого решения является довольно трудоемкой.