MikeMirzayanov's blog

2013-2014 CT S01E01: Codeforces Trainings Season 1 Episode 1
By MikeMirzayanov, 11 years ago, translation, In English

Welcome to 2013-2014 CT S01E01: Extended 2000 ACM-ICPC East Central North America Regional Contest (ECNA 2000). The training duration is 5 hours. It is opened for teams as well as for individual participants. After the end you may use the practice mode to complete problem solving. Also it will be availible as a virtual contest for whose of you who can't take part today. Please, do not cheat. Only fair play!

It is possible that the problems will be too easy for some participants, it is possible that we will add some problems.

Good luck!

  • Vote: I like it
  • +45
  • Vote: I do not like it

»
11 years ago, # |
← Rev. 4   Vote: I like it +5 Vote: I do not like it

please do not use register mode for it. I could not find any information about registration.

EDIT: I found the registration option there. Please NEGLECT the comment.

→ Reply
»
11 years ago, # |
  Vote: I like it +3 Vote: I do not like it

In problem B: "The judges input will be such that the maximum value for any poly-polygonal number will fi t in a long variable."

How i suppose to know what long are authors using? 64-bit? 32-bit?

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    By looking at the time: it's regional in year 2000

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      But in Java long was always 64 bit. Or i'm wrong?

      → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Sorry, I was thinking about C++ :)

        → Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it +15 Vote: I do not like it

    We had the same problem. All the contest I couldn't get how to solve the problem. But at the end of the contest we saw clarification and it helped.

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I saw clarification too late, but the problem is that some team get answer for this clar in the middle of the second hour and they were not public, so this is very sad...

      → Reply
»
11 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Sir , Is it possible to view the solution of other contestants after the contest gets over in these training seasons ????

→ Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I guess that there may be something wrong with the spj of Problem K. See these solutions: http://mirror.codeforces.com/gym/100227/submission/4444208 http://mirror.codeforces.com/gym/100227/submission/4442973

Their Case 3 both are wrong from my understanding. Did I misunderstand something?

→ Reply
»
11 years ago, # |
  Vote: I like it +5 Vote: I do not like it

How to solve problem K?

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it +11 Vote: I do not like it

    I guess it has something to do with the Erdős–Gallai_theorem.

    But during the contest I got AC by a naive random algorithm:

    • while List is not valid:
    • pick an element x in List randomly
    • List.append(x)
    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      Can you explain what do you mean exactly? What is the list? For what do we need to use it.

      → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        The task asks us to extend a list of number (with numbers already in it) such that the result will be a degree sequence of a simple graph. (The matrix is the adjacent of that graph)

        It's easy to check if a list of number is a degree sequence or not. (e.g. by Erdős–Gallai_theorem)

        And my solution is: while the list is not a degree sequence, extend it by an element in it randomly. You can see my code 4444583.

        → Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    You can get the solution by induction, or in other words by recurrence.

    Sort input array, pick largest and smallest element. Then build matrix of size largest x largest, where the first smallest rows and the first smallest columns contains only ones (except main diagonal).

    Then erase these two elements from array, subtract from all other elements of array a value smallest. Solve the problem for smaller array. And arrange result of smaller solution in our matrix in a right way (you can guess how yourself).

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      That was one of the approaches I tried... but I got confused on the irregularity that the diagonal zeroes cause and in the end decided to solve other problems...

      → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Doesn't seem very intuitive to me. May be you could help. So when we pick the largest and the smallest element then we set the first row(and correspondingly the first column) to 1s.
      Eg:
      if input is
      2
      4 2
      then I would build a matrix with something like this :
      0 1 1 1 1
      1 0 X X X
      1 X 0 X X
      1 X X 0 X
      1 X X X 0
      So firstly how do I fit in the smaller number in this matrix.
      Next how would I arrange my smaller solution to the larger one. For example it might be the case that the matrix size is larger than largest x + 1. In that case how do I work.
      So you could probably help by working out an example say:
      2
      2 3
      Solution:
      5
      0 1 1 1 0
      1 0 1 0 0
      1 1 0 0 1
      1 0 0 0 1
      0 0 1 1 0

      → Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Any intuition on Problem I. I really suck at Geometry !

→ Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why cant I view any solution after the contest is over. Are they not public ?

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    In Gym, you can't view others' solutions until you solve that problem first.

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it -8 Vote: I do not like it

      But without any editorial or without even viewing others solutions, how can i learn something new ?

      → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
          Vote: I like it +16 Vote: I do not like it

        You can view my solutions (I solved all problems but 2) here

        → Reply
        • »
          »
          »
          »
          »
          11 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Wow that's great.. Hope this will help me a lot.. Thanks a ton..

          → Reply
        • »
          »
          »
          »
          »
          11 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Thank you

          → Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Possibly i don't understand problem of accuracy in double. In problem L i've wrote binary search with such conditions link1/ It's got WA2. Then i got AC changed this snippet like this link2. Full AC code. Explain me please what's the difference between this snippets of code. I don't want to repeat this mistake.

→ Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve problem A ? I am stuck at it.

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    you're to find Minimum Spanning Tree with an additional rule — capacity of parking of Park .

    to solve the problem , for any subset of nodes , pick the edges from this nodes to Park ( member of this set directly goes to Park ) and run a MST algorithm on rest of graph .

    sorry for poor english :D

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it +2 Vote: I do not like it

      There is faster solution: iterate over masks which contain exactly k ones, but not include in st and then find mst. Complexity is .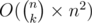

      → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        what's happen when number of edges to Park is less than K ??

        → Reply
        • »
          »
          »
          »
          »
          11 years ago, # ^ |
          ← Rev. 2   Vote: I like it +4 Vote: I do not like it

          It is obvious, you can just find mst or in the very beginning just make K = min(K, park_degree) and solve as I said above(There will be only one iteration).

          → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        This has worst case when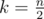 . The central binomial coefficient is asymptotic 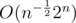, so it's still 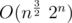asymptotically in worst-case.

        I have a solution which works in O(n 2n) time. For every subset and vertex not in it, we calculate the minimum distance of this vertex from the subset (minimum of distances of it from vertices of the subset), by taking the pre-calculated minimum from the subset without one vertex (the result is the minimum of this and the distance of our vertex from the one excluded from the subset). Now, finding MST of a given subset takes only O(N) time: we try all possible choices of the last vertex added to make this subset, and for every one of them, we already know the cost of adding it to the subset excluding this vertex. Of course, the starting subsets are the ones with at most k+1 vertices: the park and several vertices connected directly to it.

        → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I couldn't understand the solution you are proposing. I am doing something similar:

        with n park edges and k parking lots:

        iterate all masks with k ones { for each of the subsets, generate mst using them + all normal edges use the best possible mst }

        I'm getting TLE on one test case. This is O((n k)*(E*logE), E being the number of Edges used for each mst, which is probably too much for n=20 k=10, for exeample.

        Does your solution get it in (n k)*n² ? The n on n² being the park edges?

        If yes, how? Please help!

        → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      How does your solution produce the answer for the Sample Input 1 as given in the PDF ??

      → Reply