A div2
Требовалось просто найти наименьшую отсутствующую в числе цифру и сравнить результат с данным k.
B div2
Хороший отрезок либо содержит все нули, либо длина его мала. Второе следует из того, что длина отрезка не может превосходить длины последовательности {0, 1, 2, 3, 5, 8, ..., x, y} (y > 109; x < 109). Длина этой последовательности, в свою очередь, меньше 50. Тогда второй случай можно разобрать наивным алгоритмом, а второй, например, динамикой (di = 0 eсли ai ≠ 0 и di = di - 1 + 1 если ai = 0).
A div1
Заметим, что сумма в прямоугольнике (x1, y1, x2, y2) равна sum(x1, x2)·sum(y1, y2). Здесь sum(l, r) = sl + sl + 1 + ... + sr. Теперь осталось посчитать sum(l, r) для всех (l, r) и посчитать сколько отрезков дают в сумме x для всех возможных x (0 ≤ x ≤ 9·|s|). В итоге нужно пробежать по всем возможным суммам на [x1, x2] и найти 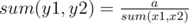 . Не стоит забывать про случай a = 0.
. Не стоит забывать про случай a = 0.
B div1
Можно считать, что Джон может x на y, если s(x) + d ≥ s(y) (не важно, если x пересекает y). Можно стандартной динамикой посчитать все возможные суммы в множествах (задача о рюкзаке). Тогда Джон должен всегда менять все свое текущее множество на другое, потому что, если он обменял подмножество x (текущее) z (подмножество) на y, можно сказать, что он поменял x to 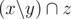 . Теперь осталось найти кратчайшую последовательность множеств a, такую, что s(ai + 1) - d ≥ s(ai) для любого i и a0 = {}. Это может быть решено следующей жадностью. ai, i > 0 максимальная корректная сумма, такая, что ai ≤ ai - 1 + d. Рассмотрим оптимальный ответ c и ответ жадности a. Пусть k — первая позиция, такая что ak ≠ ck, очевидно ak > ck (так как ak выбрано наибольшим). Затем рассмотрим q такое, что qi = ci для i ≠ k и qk = ak. q так же оптимален. Такими заменами можно получить a. Тогда a оптимально.
. Теперь осталось найти кратчайшую последовательность множеств a, такую, что s(ai + 1) - d ≥ s(ai) для любого i и a0 = {}. Это может быть решено следующей жадностью. ai, i > 0 максимальная корректная сумма, такая, что ai ≤ ai - 1 + d. Рассмотрим оптимальный ответ c и ответ жадности a. Пусть k — первая позиция, такая что ak ≠ ck, очевидно ak > ck (так как ak выбрано наибольшим). Затем рассмотрим q такое, что qi = ci для i ≠ k и qk = ak. q так же оптимален. Такими заменами можно получить a. Тогда a оптимально.
C div1
Пока не переведено.
D div1
- Возьмем случайный элемент ar из a. С вероятностью

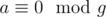 где g is ghd of a.
где g is ghd of a. - Пусть xi = gcd(ai, ar). Существует не более d различных xi, где d — количество делителей ar.
- Можно найти количество ai, таких, что
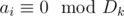 для любого k за O(d2) обычным перебором. Здесь D — множество делителей ar.
для любого k за O(d2) обычным перебором. Здесь D — множество делителей ar. - Если повторить пункт 1 x раз, то полученное решение будет корректным с вероятностью 1 - 2 - x.
Можно решать эту задачу O(n·plog + d·2plog) на итерацию (примерно в 10 раз быстрее решения выше), где plog — максимальное количество различных простых в факторизации ar. Это решение и предполагалось, но перед контестом оказалось, что можно получить ОК решением выше, если уменьшить количество итераций до минимально возможного. Уменьшать до предела количество итераций в авторском решении мы не стали.
E div1
- Найдем количество прямоугольников не более чем с k единицами внутри, пересекающих
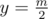 в декартовой системе координат.
в декартовой системе координат. - Можно это сделать за n2·k. Нужно найти k ближайших единиц сверху и снизк от
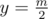 , перебрать все отрезки [l, r] такие, что 1 ≤ l ≤ r ≤ n и найти ближайшие k единиц сверху и снизу от отрезка.
, перебрать все отрезки [l, r] такие, что 1 ≤ l ≤ r ≤ n и найти ближайшие k единиц сверху и снизу от отрезка. - Это можно сделать слиянием соответствующих массивов для строк.
- Найдя ближайшие слева и справа от [l, r] k единиц можно найти количество прямоугольников, пересекающих
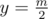 по отрезку [l, r].
по отрезку [l, r]. - Это можно сделать, перебрав количество единиц сверху, которое входит в прямоугольник. По нему однозначно восстанавливается количество единиц снизу и определяются границы, в которых может лежать верхняя и нижняя сторона прямоугольника.
- Теперь осталось поделить доску пополам и запустить этот алгоритм для половинок. При этом нужно сменить ориентацию разрезающей прямой. Нетрудно увидеть, что такой алгоритм посчитает все прямоугольники.
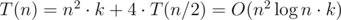 для квадратных досок. Для прямоугольных это сумма соответствующих выражений для n и m.
для квадратных досок. Для прямоугольных это сумма соответствующих выражений для n и m.

На рисунке 1 ближайшие сверху единицы (помечены черным) лежат на 4й и 2й горизонтали. Ближайшие снизу — на 5й и 7й. Тогда при k = 2 Корректных прямоугольников, которые содержат две единицы сверху и пересекают красную прямую нет. Есть 4 прямоугольника, которые содержат по одной единице сверху и снизу. На рисунках 2, 3 и 4 показано расширение имеющегося отрезка. Каждый раз требуется слить текущий массив ближайших единиц с массивом ближайших к строке единиц.










Actually, the recurrence in the problem E is T(N) = O(N2k) + 4T(N / 2). The one you've provided in the editorial has solution T(N) = O(N2k).
Oh, you are right, I'd been thought that it is n^2*k till sunday.
I don't know to solve when a=0 in problem A div 1??
Let f(0) be the number of substrings of the array that sum up to 0. So if 0 = a = sum(x1, x2)·sum(y1, y2), we know that at least one of the factors must be 0. I used inclusion-exclusion to compute the answer: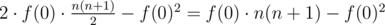 (this is the number of ways the first factor can get 0 while we don't care about the second + the number of ways the second factor can get 0 while we don't care about the first - the number of ways that both get 0).
(this is the number of ways the first factor can get 0 while we don't care about the second + the number of ways the second factor can get 0 while we don't care about the first - the number of ways that both get 0).
thank you very much !!
Can anyone explain how n*(n+1)/2 came? I am not able to understand how inclusion exclusion is working?
say , s = "102345"
matrix:
102345
000000
30____
40____
50____
x*1 size rectangles with 0 sum = 5*(5+1)/2
1*x size rectangles with 0 sum = 5*(5+1)/2
1 rect is common cell(1,1)..subtract it
you used s="10345" then made matrix according 102345 please correct it
Div1 C. (or Div2 E.), please~~
I can't find a way to prove the solution which is
Accepted.This comment
What is the c in Bdiv1? Is it the same as o is?
Can the editorial of Div1 E be more detail? Probably with a simulation of the algorithm will be better. I think this is a really good problem, and I really want to know how to solve it. Thanks the author in advance. :)
can you explain div2-C problem statement??
Well, what exactly do you need to know? The goal was to find number of all different submatrix such as sum of all its elements is equal to a. The matrix b (NxN) element (i,j) is multiplication of our string s elements i and j. I think this is almost that you need to know, but it is as well explained at original statement.
My accepted solution for DIV1-C:
Try to build answer
first, from {2, 3} primes,
then from {2, 3, 5} primes,
...,
then from {2, 3, 5, 7, 11, 13} primes.
How to try to build:
If some prime is occured less than (k+1)/2 times, then try to multiply one of the current value which is not divisible by the prime.
Six primes is enough to build answer for k = 5000.
Details: 5193128, less than 50 ms
thanks for your comment.
however, most of the codes which can solve the problem is quite short.
My code only has 51 lines, use about 15ms. // Copy from others, of course. :-(
=> http://mirror.codeforces.com/contest/365/submission/5171080
I believe there may be a more efficient way to prove that solution.
Yes, my code is not short and can be simplified. I was in hurry while writing it, and had no time for refactoring. The main purpose of my comment was to give idea about usage of no more than six primes.
My solution used 5 primes for k=5000: 5159650
There are many easier ways to solve Div2 B , and don't need to binary search.Just a simple dynamic programming .
For problem B div2 there is a much simpler way to do that by dp. for problem B div1 first part of it can be done by adding number to all previous sum we got because we can't have more than 5e5 number maximum. why making it so complicated?!
You approach for problem b div1 is similar to mine. It's not complicated, what are you talking about? What about div2 b, you are right I will add that to post.
For Div1 B, I'm just saying we can use brute force instead on knapsack. that's all. tnx for your great problems.
in problem A div 1 why maximum sum of sequence must be 9*|S|? Can anyone explain me that?
because every character of string is between 0 to 9 so the maximum sum is size of string times 9
I don't understand the proof for the C in div1, especially for the item2, can someone tell me about these ? thanks!!(sorry for my poor English)
I think you should look at example (divisors of 216)
You can see, that considered set is in the first column. 3, 6, 9, 12 are divisible by 3 and 2, 4, 6, 8, 12 is divisible by 2. So, it's beautiful set. Has it become more clear?
In div1-D, what you should say is that you compute the number of elements ai that x divides for all x which are divisors of ar, not just for all x which arise as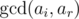 for some i. (The latter is a subset of the former.) For example, consider this testcase: 1, 1, 1, 2·3·5, 2·3·7, 2·5·7. If you pick ar = 2·3·5 for example, you must consider x = 2 (the actual ghd), which is not a gcd of any element and ar (the gcds are: 1, 1, 1, 2·3·5, 2·3, 2·5). This is of course still doable in
for some i. (The latter is a subset of the former.) For example, consider this testcase: 1, 1, 1, 2·3·5, 2·3·7, 2·5·7. If you pick ar = 2·3·5 for example, you must consider x = 2 (the actual ghd), which is not a gcd of any element and ar (the gcds are: 1, 1, 1, 2·3·5, 2·3, 2·5). This is of course still doable in 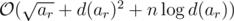 .
.
Yes, you are right, I will write this item carefully.
I think the probability-solution for the problem D-div1 isn't appreciated. Let's consider this case
I think the probability-solution will give
1but the correct answer is2Do you have any arguments? Is my calculation of probabillity wrong?
On your test my solution works with probabillity 1.
Because sometimes, gcd of two elements is not a result.
For example:
Oh, yes, I got it. I've fixed explanations.
^_^. Thus, I think you should update the test data because some wrong-solutions still got accepted :D
For example: http://mirror.codeforces.com/contest/364/submission/5199045
I think, that's correct solution. Why it's wrong?
Поясните, пожалуйста, тест№3 для Адив2.
1 0 1000000000
Данное число, по-моему, является 1-хорошим, т.к. в нем есть нули и единицы (Назовем число k-хорошим, если оно содержит все цифры, не превосходящие k (0, ..., k)). И оно не является 0-хорошим, т.к. содержит единицу, почему же тогда ответ 1, а не 0? Мое решение — http://mirror.codeforces.com/contest/365/submission/5625792
Я не умею писать условия, но формально вы поняли неверно. Число называется хорошим, если содержит все цифры от 0 до k. Из этого не следует, что число, содержащее k+1, не может быть k хорошим. Но следует, что число, не содержащее хотя бы одну цифру из {0, ..., k} не будет являться хорошим. Так стало понятнее?
Да, точно, спасибо. Я неправильно понял.
Can anyone explain the div 1 5th problem with a picture ? since the original picture is not available now
Errichto Can you please explain your solution for div1 A ?
Do I even know this problem? :D there is no link or statement in this editorial.
Sorry I did not notice, here is the link to the Problem
In div2B, why do we need binary search? Wouldn't it be done by simple brute force?
For problem D div1 can anyone tell me how to avoid getting wa for the last test case and the specific reason why for that test case my randomized algo is not working properly? 265153694
really liked problem C