Hello, I've made a video-editorial for the problem Div.2 E (Div.1 C) from the latest contest.
https://www.youtube.com/watch?v=lST0djhfxfk
Thanks the authors for a cool contest!
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
Hello, I've made a video-editorial for the problem Div.2 E (Div.1 C) from the latest contest.
https://www.youtube.com/watch?v=lST0djhfxfk
Thanks the authors for a cool contest!
Hello, I've made a video-editorial for the problem Div.2 D (Div.1 B) from the yesterday's contest.
https://www.youtube.com/watch?v=0pQjbLOQL-c
Thanks Arti1990 for this controversial problem!
Hello, here's a video-editorial for problems F and G from the latest "CodeTON" contest with a little motivational speech in the beginning.
https://www.youtube.com/watch?v=fJ_0M2DDEvw
Thanks RDDCCD and the TON Foundation for a cool contest!
Hello, I've made a video-editorial for problems Div.2 B–E (Div.1 A–C) from today's contest.
https://www.youtube.com/watch?v=VwY7QzStMk4
Thanks the authors for a cool contest!
Hello, I've made a full video editorial for the latest CF div. 2 round / first three problems from div. 1.
https://www.youtube.com/watch?v=-ksLcl2tQCg
Thanks to all the authors for a cool contest!
Hello, I've made a video-editorial for problems Div.2 C–E (Div.1 A–C) from today's contest.
https://www.youtube.com/watch?v=VdRo42OEJIY
Thanks the authors for a cool contest!
Hello, I've made a video-editorial for problems Div.2 C–E (Div.1 A–C) from yesterday's contest.
https://www.youtube.com/watch?v=k6dxqX3JIhM
Thanks the authors for a cool contest!
Hello, I've made a video-editorial for problems Div.2 B–E (Div.1 A–C) from today's contest.
https://www.youtube.com/watch?v=Gu3GbiMUSAw
Thanks the authors for a cool contest!
Hello, I've made a video-editorial for problems D–E from yesterday's contest.
https://www.youtube.com/watch?v=mGgV3eHhVoI
Thanks the authors for a cool contest!
Hello, here's a video-editorial for problems B–E from today's contest.
https://www.youtube.com/watch?v=c9A-fO6fPXQ
Thanks RDDCCD and the TON Foundation for a cool contest!
Hello, I've made a full video editorial for the latest CF round. I'm a bit late, but I can compensate that by having a super-solution for problem E, which is faster than the authors' and also easier in my opinion.
https://www.youtube.com/watch?v=i1i_7lqnGwA
Thanks to all the authors for a cool contest!
Hello, I've made a video-editorial for problem F from yesterday's contest, but if the constraints were much higher. As I use Diophantine equations there, I've decided to make a separate short video about them. So here they are both:
https://www.youtube.com/watch?v=Yn5GAoGHTsM
https://www.youtube.com/watch?v=IDmDg6PoVug
Thanks the developers for a cool contest!
Hello, here's a video-editorial for problems B–E from yesterday's contest.
https://www.youtube.com/watch?v=ch-yS2jqmKQ
Thanks Nebius for a cool contest!
Я нашёл эти статьи, в них уже это описано:
https://mirror.codeforces.com/blog/entry/72527
https://mirror.codeforces.com/blog/entry/46620
Они обе очень хорошие. но я хотел написать более сжатый пост конкретно про обратный остаток, потому что он требуется во многих задачах, даже не связанных с теорией чисел.
Есть два целых числа A и B. Предположим, вы знаете, что A делится на B. Но они очень большие, поэтому вы знаете только их остатки по модулю некоторого простого числа M: A % M and B % M. Вы хотели бы узнать остаток их частного – (A / B) % M. Но (A % M) может не делиться на(B % M). Что делать?
Такой вопрос нередок в комбинаторных задачах, например, при подсчёте биномиальных коэффициентов, когда нужно поделить n! на k! и (n - k)!.
Короткий ответ – вам нужно вычислить B в степени M - 2 по модулю M (с помощью бинарного возведения в степень). Получившееся число называется обратным остатком B. Теперь вы можете умножить A на него, чтобы по сути разделить его на B.
Примечание: это работает только если B % M – не 0, а M – простое.
#include <bits/stdc++.h>
using namespace std;
const int mod = 998244353;
int bin_exp(int a, int b) {
if (b == 0) {
return 1;
}
if (b % 2) {
return bin_exp(a, b - 1) * 1LL * a % mod;
}
int res = bin_exp(a, b / 2);
return res * 1LL * res % mod;
}
int inv(int a) {
return bin_exp(a, mod - 2);
}
int32_t main() {
ios_base::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int a, b;
cin >> a >> b;
cout << a * 1LL * inv(b) % mod << '\n';
}
#include <bits/stdc++.h>
using namespace std;
#define int int64_t
const int mod = 998244353;
int bin_exp(int a, int b) {
if (b == 0) {
return 1;
}
if (b % 2) {
return bin_exp(a, b - 1) * a % mod;
}
int res = bin_exp(a, b / 2);
return res * res % mod;
}
int inv(int a) {
return bin_exp(a, mod - 2);
}
int32_t main() {
ios_base::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int a, b;
cin >> a >> b;
cout << a * inv(b) % mod << '\n';
}
Это известная формула, опирающаяся на малую теорему Ферма и на тот факт, что каждый ненулевой элемент кольца остатков по простому модулю имеет ровно один обратный элемент по умножению. Если вы хотите узнать больше, вы можете прочитать упомянутые мною статьи.
Hello, I've recorded another detailed video-editorial for problems div.2 C–F / div.1 A–D from yesterday's contest.
https://www.youtube.com/watch?v=ch-yS2jqmKQ
Thanks for all the authors for this cool contest!
Hello, I've recorded a detailed video-editorial for problems C, D and E from today's div.2 contest.
https://www.youtube.com/watch?v=jFSUQmxCoUI
Thanks MateoCV for a cool contest!
Hello, I've recorded a video-editorial for problem F from the latest div.1 contest, where I apply the method which I call "narrow down the choice".
https://www.youtube.com/watch?v=lOkpzBAbFIE
If you want, I'll make a blog entry where I tell in details about this method.
Допустим, вы хотите для некоторых n и k найти сумму:
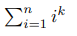
Вот известные формулы для первых нескольких k:
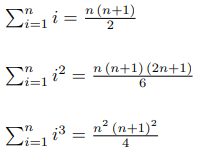
Допустим, вы забыли их. Что делать? К счастью, существует простой алгоритм для генерации этих формул.
Прежде всего докажем теорему.
Предположим, что для каждого целого неотрицательного n:
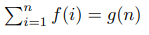
где f и g – многочлены. Тогда для некоторой константы c:
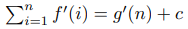
Для каждого целого положительного n верно:
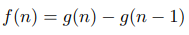
Эти два многочлена равны в бесконечном количестве точек, а значит, они тождествены. Что позволяет нам сказать:
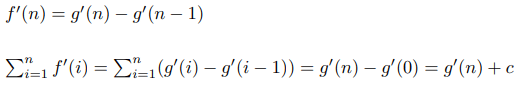
Допустим, мы хотим найти формулу для суммы квадратов. Тогда, используя нашу теорему, можно построить такой алгоритм:
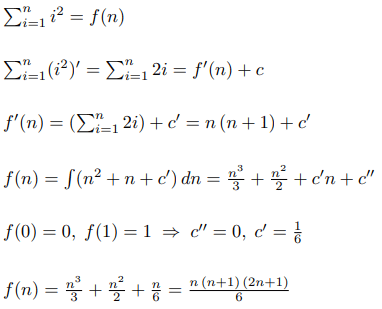
Теперь проделаем тот же алгоритм для суммы кубов:
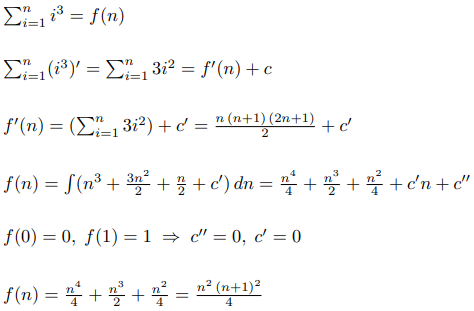
Hello, I've recorded a video-editorial for D1 and D2 from today's contest, where I apply my method of "Process-DP".
https://www.youtube.com/watch?v=oOyPQL16x1M
You can read about this method in details here:
Нет, я не имею в виду Convex Hull-оптимизацию и оптимизацию Кнута. Я имею в виду более простые и распространённые методы.
Это продолжение моей серии постов о ДП, чтобы понимать обозначения, читайте пролог.
Очень часто после построения графа динамики можно обнаружить, что переходы в то или иное состояние ведут не из случайного набора вершин, а из некоторого отрезка по одному из параметров. Например, из состояний dp[i][j], при некотором константном i и при j, лежащим в отрезке [a, b].
В таком случае можно не реализовывать каждый переход в отдельности, а реализовать все скопом. Если под реализацией перехода понимается прибавление из dp[A] в dp[B], то можно воспользоваться префиксной суммой. Если же нам нужно найти наилучший переход в dp[B], то можно воспользоваться деревом отрезков.
AtCoder DP Contest: Задача M Найти количество целочисленных последовательностей длины n, где i-е число от 0 до a[i], а сумма чисел равна k.
Решим методом симуляции процесса. Рассмотрим процесс выписывания по одному числу последовательности. Параметрами процесса будут:
Сколько мы уже выписали чисел.
Сумма выписанных чисел.
Значением динамики dp[i][j] будет количество путей процесса, ведущих в данное состояние.
Количество переходов из одного состояния равно O(k), общее количество переходов – O(n k^2), слишком долго.
Рассмотрим, откуда ведут переходы в состояние dp[i][j]. Очевидно, из dp[i - 1][l], где l принадлежит отрезку [max(0, j - a[i - 1]), j].
Значит, перед тем, как считать слой i, можно насчитать префиксные суммы на слое i - 1, чтобы считать dp[i][j] за O(1).
#include <bits/stdc++.h>
#define int int64_t
using namespace std;
int mod = 1e9 + 7;
int32_t main() {
ios_base::sync_with_stdio(false);
int n, k;
cin >> n >> k;
vector<int> a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
vector<int> dp(k + 1); // текущий слой (мнимый параметр)
dp[0] = 1;
for (int i = 0; i < n; i++) {
vector<int> sum(dp.size() + 1); // префикс-суммы текущего слоя
for (int j = 0; j < dp.size(); j++) {
sum[j + 1] = sum[j] + dp[j];
}
vector<int> new_dp(k + 1); // следующий слой
for (int j = 0; j <= k; j++) {
new_dp[j] = (sum[j + 1] - sum[max(int64_t(0), j - a[i])]) % mod;
}
dp = new_dp;
}
cout << dp[k] << endl;
}
Вернёмся к задаче из прошлой части моего блога.
543A - Пишем код Есть n программистов, они должны написать m строк кода, сделав не более b ошибок. i-й программист совершает a[i] ошибок за строку. Сколько есть способов это сделать? (Два способа различаются, если различается количество строк, написанных одним из программистов).
Вспомним самое первое решение: определим процесс, где за один шаг мы назначаем очередному программисту количество написанных им строк. Параметрами будут:
Количество пройденных программистов.
Суммарное количество написанных строк.
Суммарное количество сделанных ошибок.
Значением динамики dp[i][j][k] будет количество путей процесса, ведущих в данное состояние.
Тогда состояний всего получается O(n m b), а переходов из одного состояния – O(m), значит всего переходов – O(n m^2 b), что слишком много.
Но давайте рассмотрим, из каких состояний есть переход в состояние dp[i][j][k]. Если последний шаг был "i - 1-й программист написал x строк кода", то переход был из состояния dp[i - 1][j - x][k - x * a[i - 1]] (где x >= 0).
То есть состояния, из которых ведёт переход, расположены на некоторой прямой в таблице i - 1-ого слоя, и в общем случае сумму всех таких значений можно за O(1) вычислить из аналогичной суммы для состояния dp[i][j - 1][k - a[i - 1]].
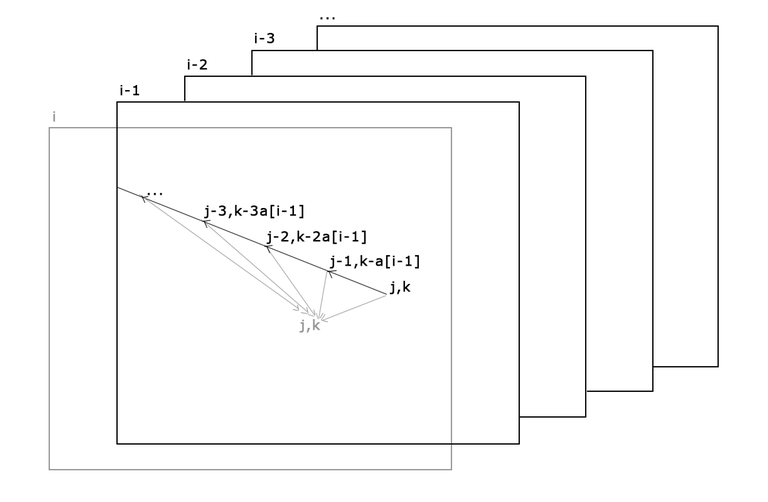
После некоторых упрощений код выглядит так:
#include <bits/stdc++.h>
using namespace std;
#define int int64_t
int mod;
void add(int& a, int b) { // вместо (a += b) %= mod
a += b;
if (a >= mod) {
a -= mod;
}
}
int32_t main() {
ios_base::sync_with_stdio(0);
int n, m, b;
cin >> n >> m >> b >> mod;
vector<int> a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
vector<vector<int>> dp(m + 1, vector<int>(b + 1)); // текущий слой
dp[0][0] = 1;
for (int i = 0; i < n; i++) { // переход от слоя i к i + 1
for (int j = 0; j < m; j++) {
for (int k = 0; k <= b - a[i]; k++) {
add(dp[j + 1][k + a[i]], dp[j][k]);
}
}
}
int ans = 0;
for (int k = 0; k <= b; k++) {
add(ans, dp[m][k]);
}
cout << ans << endl;
}
Эта техника стара, как мир. Если один из параметров слишком большой, а значение наоборот ограничено, можно попробовать поменять их ролями.
AtCoder DP Contest: Задача E Есть n объектов, i-й имеет вес w[i] и цену v[i]. Какая максимальная сумма цен по всем наборам объектов с суммой весов не более m? В этой версии задачи n <= 100, m <= 10^9, v[i] <= 10^3.
Возьмём решение из предыдущей части блога: рассмотрим процесс, где на каждом шагу рассматривается очередной объект и либо выбирается, либо пропускается, параметрами процесса будут:
Количество рассмотренных объектов.
Суммарный вес выбранных объектов.
Значением динамики будет наибольшая сумма стоимостей выбранных объектов при данном состоянии процесса.
При данных ограничениях, максимальное значение второго параметра будет 10^9, а максимальное значение динамики – 10^5, поэтому имеет смысл поменять их ролями. Процесс будет тем же самым, но параметрами будут:
Количество рассмотренных объектов.
Суммарная стоимость выбранных объектов.
Значением динамики будет наименьшая сумма весов выбранных объектов при данном состоянии процесса.
В конце мы рассмотрим наибольшую сумму стоимостей объектов из числа тех, для которых минимальный суммарный вес не больше W.
#include <bits/stdc++.h>
using namespace std;
#define int int64_t
void relax(int& a, int b) {
a = min(a, b);
}
const int max_v = 1e5;
int32_t main() {
ios_base::sync_with_stdio(0);
int n, m;
cin >> n >> m;
vector<int> w(n), v(n);
for (int i = 0; i < n; i++) {
cin >> w[i] >> v[i];
}
vector<int> dp(max_v + 1, 2e18); // если в состояние не ведёт ни один путь, минимальной суммой считается inf
dp[0] = 0;
for (int i = 0; i < n; i++) {
vector<int> new_dp = dp; // автоматически реализуем все переходы первого вида
for (int j = 0; j <= max_v - v[i]; j++) {
// фиксируем состояние dp(i)[j], где i мнимое
relax(new_dp[j + v[i]], dp[j] + w[i]); // переход второго вида
}
dp = new_dp; // переходим от слоя i к i + 1
}
int ans = 0;
for (int i = 0; i <= max_v; i++) {
if (dp[i] <= m) {
ans = i;
}
}
cout << ans << endl;
}
Иногда мы можем заметить о неких параметрах, что нам необязательно знать значение каждого, а достаточно следить за некой их комбинацией. Например, если в конце мы делаем проверку на то, что сумма двух параметров не должна превышать некоторое значение, то возможно у нас получится заменить эти два параметра на один, равный их сумме.
19B - Кассир Есть n товаров, у каждого есть цена c[i] и время обработки t[i]. Найдите множество товаров с минимальной суммарной ценой такое, что их суммарное время обработки не меньше количества остальных товаров.
Рассмотрим процесс, где на каждом шагу рассматривается очередной товар и либо выбирается, либо пропускается. Параметрами процесса будут:
Количество рассмотренных товаров.
Суммарное время обработки выбранных товаров.
Количество невыбранных товаров.
Значением динамики будет минимальная суммарная стоимость выбранных товаров при данном состоянии процесса.
По итогу нас интересуют состояния dp[n][j][k], где j >= k. Так как k <= n, мы будем считать, что если параметр j достиг n, то в дальнейшем нет смысла его повышать, так что все состояния процесса при больших значениях параметра j будем записывать, будто j = n.
Таким образом количество состояний равно O(n^3), как и количество переходов, что не проходит под ограничения.
Рассмотрим подробнее, куда ведут переходы из состояния dp[i][j][k]: в случае выбора товара – в dp[i + 1][j + t[i]][k], а в случае пропуска – в dp[i + 1][j][k + 1].
Заметим, что в первом случае разность второго и третьего параметров просто увеличивается на t[i], во втором случае – уменьшается на 1, а в конце нужно отсечь те состояния, где эта разность неотрицательна, следовательно вместо каждого этого параметра по отдельности, можно следить за их разностью.
Для удобства вместо j - k будем следить за j + i - k (чтобы параметр был неотрицательным, т. к. k <= i), тогда при выборе товара параметр увеличивается на t[i] + 1, а при пропуске не изменяется.
Так как в конце отсекаются состояния, где этот параметр не меньше n, при этом он ни при каком переходе не уменьшается, то можно аналогично предыдущему решению записывать состояния с j + i - k > n в dp[i][n].
Таким образом, количество состояний и переходов оба равны O(n^2).
#include <bits/stdc++.h>
using namespace std;
#define int int64_t
void relax(int& a, int b) {
a = min(a, b);
}
int32_t main() {
ios_base::sync_with_stdio(0);
int n;
cin >> n;
vector<int> t(n), c(n);
for (int i = 0; i < n; i++) {
cin >> t[i] >> c[i];
}
vector<int> dp(n + 1, 2e18); // текущий слой (мнимый параметр)
dp[0] = 0;
for (int i = 0; i < n; i++) {
vector<int> new_dp = dp; // применяем переходы второго вида
for (int j = 0; j <= n; j++) {
relax(new_dp[min(n, j + t[i] + 1)], dp[j] + c[i]);
}
dp = new_dp; // переходим к следующему слою
}
cout << dp[n];
}
Если хотите узнать больше, я напоминаю, что даю частные уроки по спортивному программированию, цена – 1800 руб/ч. Пишите мне в Telegram, Discord: rembocoder#3782, или в личные сообщения на CF.
Казалось бы, по бинпоиску написано столько материалов, что все должны знать, как писать его, однако в каждом материале похоже рассказывается свой подход, и я вижу, что люди теряются и допускают ошибки в такой простой штуке. Поэтому я хочу рассказать о подходе, который нахожу наиболее элегантным. Из всего многообразия статей, я увидел свой подход только в этом комментарии (но менее обобщённый).
Предположим, вы хотите найти последний элемент в отсортированном массиве, меньший x, и просто храните отрезок кандидатов на ответ [l, r]. Если вы напишете:
int l = 0, r = n - 1; // отрезок кандидатов
while (l < r) { // больше одного кандидата
int mid = (l + r) / 2;
if (a[mid] < x) {
l = mid;
} else {
r = mid - 1;
}
}
cout << l;
...вы наткнётесь на проблему: предположим, l = 3, r = 4, тогда mid = 3. Если a[mid] < x, вы попадёте в цикл (на следующей итерации отрезок будет снова [3, 4]).
Ладно, это можно исправить округлением mid вверх – mid = (l + r + 1) / 2. Но есть ещё одна проблема: что если в массиве нет таких элементов? Нам потребуется дополнительная проверка на этот случай. В результате, мы получили довольно уродливый код, который тяжело обобщить.
Давайте обобщим нашу задачу. У нас есть утверждение о целом числе n, которое истинно для целых чисел меньше некоторой границы, но потом всегда остаётся ложным как толькоn превысит её. Мы хотим найти последнееn, для которого утверждение истинно.
Прежде всего, мы будем использовать полуинтервалы вместо отрезков (одна граница включительная, другая – нет). Полуинтервалы вообще очень полезны, элегантны и общеприняты в программировании, я рекомендую использовать их по возможности. В этом случае мы выбираем некое маленькое l, для которого мы знаем, что утверждение истинно и некое большое r, для которого мы знаем, что оно ложно. Тогда диапазоном кандидатов будет [l, r).
Моим код для этой задачи было бы:
int l = -1, r = n; // полуинтервал [l, r) кандидатов
while (r - l > 1) { // больше одного кандидата
int mid = (l + r) / 2;
if (a[mid] < x) {
l = mid; // теперь это наибольшее, для которого мы знаем, что это истинно
} else {
r = mid; // теперь это наименьшее, для которого мы знаем, что это ложно
}
}
cout << l; // в конце остаётся диапозон [l, l + 1)
Бинпоиск будет проверять только числа строго между изначальными l и r. Это значит, что он никогда не проверит условие для l и r, он поверит вам, что для l это истинно, а для r – ложно. Здесь мы считаем -1 корректным ответом, который соответствует случаю, когда ни один элемент массива не меньше x.
Заметьте, что у меня в коде нет "+ 1" или "- 1", и мне не нужны дополнительные проверки, и попадание в цикл невозможно (т. к. mid строго между текущими l и r).
Единственная вариация, которую вам надо держать в голове – это что в половине случаев вам нужно будет найти не последнее, а первое число, для которого нечто выполняется. В этом случае утверждение должно быть всегда ложно для меньших чисел и всегда истинно, начиная с некоторого числа.
Мы будем делать примерно то же самое, но теперьr будет включительной границей, а l – не включительной. Другими словами, l теперь – некоторое число, для которого мы знаем, что утверждение ложно, а r – некоторое, для которого мы знаем, что оно истинно. Предположим, я хочу найти первое число n, для которогоn * (n + 1) >= x (x положительно):
int l = 0, r = x; // полуинтервал (l, r] кандидатов
while (r - l > 1) { // больше 1 кандидата
int mid = (l + r) / 2;
if (mid * (mid + 1) >= x) {
r = mid; // теперь это наименьшее, для которого мы знаем, что это истинно
} else {
l = mid; // теперь это наибольшее, для которого мы знаем, что это ложно
}
}
cout << r; // в конце остаётся диапозон (r - 1, r]
Только будьте осторожны с выбором r, слишком большое может привести к переполнению.
1201C - Максимальная медиана Вам дан массив a нечётной длины n и за один шаг можно увеличить один элемент на 1. Какую наибольшую медиану массива можно достичь за k шагов?
Рассмотрим утверждение о числе x: мы можем сделать медиану не меньше x за не более, чемk шагов. Конечно, это всегда истинно до некоторого числа, а затем всегда ложно, поэтому можно использовать бинпоиск. Так как нам нужно последнее число, для которого это истинно, мы будем использовать обычный полуинтервал [l, r).
Чтобы проверить данное x, мы можем воспользоваться свойством медианы. Медиана не меньше x тогда и только тогда, когда не менее половины всех элементов не меньше x. Конечно, оптимальным способом добиться этого будет взять наибольшую половину элементов и сделать их не меньше x.
Конечно, можно достичь медиану не менее 1 при данных ограничениях, так что l будет равно1. Но даже если есть только один элемент, равный 1e9 и k тоже равно1e9, мы всё равно не сможем добиться медианы 2e9 + 1, так что r будет равно 2e9 + 1. Реализация:
#define int int64_t
int n, k;
cin >> n >> k;
vector<int> a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
sort(a.begin(), a.end());
int l = 1, r = 2e9 + 1; // полуинтервал [l, r) кандидатов
while (r - l > 1) {
int mid = (l + r) / 2;
int cnt = 0; // необходимое количество шагов
for (int i = n / 2; i < n; i++) { // идём по наибольшей половине
if (a[i] < mid) {
cnt += mid - a[i];
}
}
if (cnt <= k) {
l = mid;
} else {
r = mid;
}
}
cout << l << endl;
Надеюсь, я разъяснил кое-что, и часть из вас переключится на эту имплементацию. Для уточнения, иногда другие имплементации могут оказаться более подходящими, например, в интерактивных задачах – когда нам нужно мыслить в терминах интервала поиска, а не в терминах первого/последнего числа, для которого что-то выполняется.
Я напоминаю, что даю частные уроки по спортивному программированию, цена – $30/ч. Пишите мне в Telegram, Discord: rembocoder#3782, или в личные сообщения на CF.
Здравствуйте. Это пролог к моим предыдущим постам, в котором я коротко введу читателя в терминологию динамического программирования. Это не исчерпывающий гайд, а лишь вступление, чтобы у неподготовленного читателя могла сложиться полная картина, какой её вижу я.
Динамическое программирование – способ решения задачи путём её параметризации таким образом, чтобы ответ на задачу при одних значениях параметров помогал в нахождении ответа при других значениях параметров; а затем нахождения ответа при всех допустимых значениях параметров.
Состояние ДП – конкретный набор значений для каждого параметра (конкретная подзадача).
Значение ДП – ответ для конкретного состояния (подзадачи).
Переход из состояния A в состояние B – пометка, означающая, что для того, чтобы узнать значение для состояния B, требуется знать ответ для состояния A.
Реализовать переход из A в B – некое действие, проводимое, когда ответ для состояния A уже известен, удовлетворяющее условию: если реализовать все переходы, ведущие в B, то мы узнаем ответ для B. Само действие может отличаться от задачи к задаче.
Базовое состояние ДП – состояние, в которое нет переходов. Ответ для такого состояния ищется напрямую.
Граф ДП – граф, в котором каждая вершина соответствует состоянию, а каждое ребро – переходу.
Чтобы решить задачу, необходимо составить граф ДП – определиться, какие имеются переходы и как их реализовывать. Само собой, в графе ДП не должно быть циклов. Затем нужно найти ответ для всех базовых состояний и начать реализовывать переходы.
Мы можем реализовывать переходы в любом порядке, если выполняется следующее правило: не реализуйте переход из состояния A раньше перехода в состояние A. Но чаще всего используются два способа: с переходами назад и с переходами вперёд.
Реализация с переходами назад – проходим по всем вершинам в порядке топологической сортировки и для каждой фиксированной вершины реализуем все переходы в неё. Иными словами, на каждом шаге берём не посчитанное состояние и считаем для него ответ.
Реализация с переходами вперёд – проходим по всем вершинам в порядке топологической сортировки и для каждой фиксированной вершины реализуем все переходы из неё. Иными словами, на каждом шаге берём посчитанное состояние и реализуем переходы из него.
В разных случаях удобны разные способы реализации переходов, в том числе можно использовать и "кастомные".
В отличие от предыдущих постов, я не буду углубляться в то, как придумать решение, лишь продемонстрирую введённые понятия в действии.
AtCoder DP Contest: Задача K Два игрока по очереди достают из кучи камни, за один ход можно достать a[0], ..., a[n - 2] или a[n - 1] камней. Изначально в куче k камней. Кто выигрывает при оптимальное игре?
Параметром ДП будет i – сколько камней изначально находится в куче.
Значением ДП будет 1, если в этой подзадаче выигрывает первый игрок, иначе – 0. Ответы будут храниться в массиве dp[i]. Зачастую само состояние i = x для краткости обозначается dp[x], я тоже буду пользоваться этим обозначением. Назовём позицию выигрышной, если из неё побеждает тот, чей сейчас ход. Позиция выигрышная тогда и только тогда, когда из неё есть ход в проигрышную, т. е.dp[i] = 1 если для какого-то j (0 <= j < n, a[j] <= i) dp[i - a[j]] = 0, иначе dp[i] = 0.
Таким образом, будут существовать переходы из dp[i - a[j]] в dp[i] для всех i и j (a[j] <= i <= k, 0 <= j < n).
Реализацией перехода из A в B в данном случае будет: если dp[A] = 0, присвоить dp[B] = 1. По умолчанию каждое состояние считается проигрышным (dp[i] = 0).
Базовым состоянием в данном случае будет dp[0] = 0.
Граф динамики в случае k = 5, a = {2, 3}:
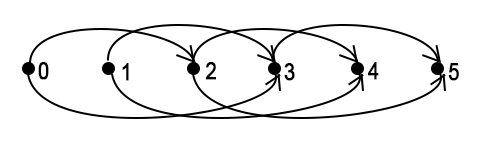
В этом коде я использую реализацию с переходами назад.
#include <bits/stdc++.h>
using namespace std;
#define int int64_t
int32_t main() {
ios_base::sync_with_stdio(0);
int n, k;
cin >> n >> k;
vector<int> a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
vector<bool> dp(k + 1);
for (int i = 1; i <= k; i++) { // фиксируем состояние
for (int j = 0; j < n; j++) { // фиксируем переход в него
if (a[j] > i) {
continue;
}
if (!dp[i - a[j]]) { // реализуем переход
dp[i] = 1;
}
}
}
cout << (dp[k] ? "First" : "Second");
}
Без оптимизаций сложность алгоритма равна количеству переходов, в этом случае это O(nk).
AtCoder DP Contest: Задача I Есть n монет, i-я монета падает решкой с вероятностью p[i]. Найти вероятность, что число решек будет больше числа орлов, если подбросить все монеты по одному разу.
Параметрами ДП будет i – сколько первых монет мы рассматриваем, и j – сколько должны выпасть решкой.
Значением ДП будет вероятность, что ровно j упадут решкой, если подбросить первые i монет, оно будет храниться в массиве dp[i][j]. При i > 0 возможны два исхода, как могло выпасть j монет решкой: либо среди первых i - 1 выпадет решкой j - 1 и следующая тоже выпадет решкой: это возможно при j > 0, вероятность этого dp[i - 1][j - 1] * p[i - 1]; либо среди первых i - 1 выпадет решкой j, а следующая не выпадет решкой: это возможно при j < i, вероятность этого dp[i - 1][j] * (1 - p[i - 1]). dp[i][j] будет суммой этих двух вероятностей.
Таким образом, будут существовать переходы из dp[i][j] в dp[i + 1][j + 1] и в dp[i + 1][j] для всех i и j (0 <= i < n, 0 <= j <= i).
Реализацией перехода из A в B в данном случае будет: прибавить ответ для состояния A, помноженный на вероятность данного перехода, к ответу для состояния B. По умолчанию вероятность попасть в каждое состояние считается равной 0 (dp[i][j] = 0).
Это решение использует подход с симуляцией процесса, чтобы лучше его понять, читайте мой пост.
Мы симулируем процесс, где на каждом шаге подбрасывается одна монетка слева направо. dp[i][j] – суммарная вероятность всех путей, приводящих в данное состояние процесса. Изначально нам не известно ни одного пути, приводящего в какое-либо состояние, кроме как "пустого" пути в начальное состояние. Именно поэтому изначально все dp[i][j] равны 0, кроме dp[0][0], которое равно 1. При реализации перехода из A в B, мы обнаруживаем целый класс путей в состояние B, которые проходят через A, и прибавляем их суммарную вероятность к dp[B].
Базовым состоянием в данном случае будет dp[0][0] = 1.
Граф динамики в случае n = 3:
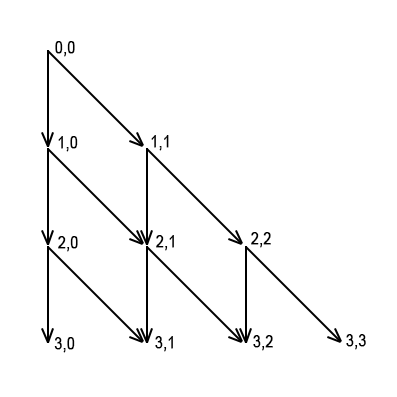
В этом коде я использую реализацию с переходами вперёд.
#include <bits/stdc++.h>
using namespace std;
#define int int64_t
int32_t main() {
ios_base::sync_with_stdio(0);
int n;
cin >> n;
vector<double> p(n);
for (int i = 0; i < n; i++) {
cin >> p[i];
}
vector<vector<double>> dp(n + 1, vector<double>(n + 1));
dp[0][0] = 1; // базовое состояние
for (int i = 0; i < n; i++) {
for (int j = 0; j <= i; j++) { // фиксируем состояние
dp[i + 1][j + 1] += dp[i][j] * p[i]; // реализуем
dp[i + 1][j] += dp[i][j] * (1 - p[i]); // переходы из него
}
}
double ans = 0;
for (int i = n / 2 + 1; i <= n; i++) {
ans += dp[n][i];
}
cout.precision(10);
cout << ans;
}
Число переходов (и таким образом, сложность алгоритма) в этом случае равно O(n^2).
После прочтения этой статьи я советую прочитать мои предыдущие два поста. В них я рассказываю про два вида динамического программирования, и это разделение мне кажется принципиальным для дальнейшего понимания.
Два вида динамического программирования: Симуляция процесса
Как решать задачи на ДП: Обычный подход
Если хотите узнать больше, я напоминаю, что даю частные уроки по спортивному программированию, цена – $25/ч. Пишите мне в Telegram, Discord: rembocoder#3782, или в личные сообщения на CF.
Привет! В прошлом посте я ввёл два вида динамического программирования: обычное и с симуляцией процесса. В нём я рассказал, как решать задачи на ДП, используя симуляцию процесса, пожалуйста, прочитайте, если пропустили, чтобы понимать разницу. Сейчас же я хочу поговорить о хитростях, которые помогают мне при решении задач на ДП обычным подходом.
Тогда как в симуляции процесса нам требовалось изобрести некий процесс, который бы строил нам необходимые объекты, в обычном подходе мы будем работать с объектами напрямую. Каждое состояние ДП (т. е., набор значений по каждому параметру) будет соответствовать некому классу желаемых объектов, а соответствующее значение в таблице ДП будет содержать информацию об этом классе, что в действительности эквивалентно формулировке через подзадачи, описанной в предыдущем посте.
В этом посте я сосредоточусь на том, как придумывать переходы в ДП с обычным подходом, если вы уже определились с параметрами. Общий план такой:
Сформулируйте, что является рассматриваемым объектом задачи. Желательно отобразите его визуально.
Разбейте рассматриваемые объекты на классы и постарайтесь покрыть каждый класс набором переходов к меньшим подзадачам.
Сначала покройте то, что покрывается очевидным образом, а затем сфокусируйтесь конкретно на том, что осталось.
informatics.msk.ru: Шаблон с ? и * Есть две строки, называемые "шаблонами", состоящие из латинских букв и знаков '*' и '?'. Строка считается подходящей под шаблон, если её можно получить из шаблона, заменив каждый '?' на некую букву и каждую '*' на некую последовательность букв (возможно пустую). Найдите длину кратчайшей строки, подходящей под оба шаблона.
Снова, если вы очень хотите, эту задачу можно решить и симуляцией процесса, но по-моему решение будет довольно неестественным. Так что продолжим с обычным подходом с подзадачами, а именно с подходом с классификацией объектов.
Давайте параметризуем эту задачу. Распространённым способом это сделать в таких задачах будет спросить тот же вопрос про некие два префикса шаблонов. То есть, "какая длина кратчайшей строки, подходящей под оба шаблона, но если мы рассматриваем толькоi символов первого и j символов второго шаблона?". Каждое состояние ДП будет соответствовать данному классу строк, а соответствующее значение в таблице ДП будет хранить длину кратчайшей такой строки.
Теперь предположим, что мы находим ответ для каждого такого вопроса в таком порядке, что когда мы обрабатываем состояние dp[i][j], мы уже знаем ответы для всех меньших пар префиксов (мы знаем все dp[i'][j'], гдеi' <= i и j' <= j кроме самой dp[i][j]). Как это знание поможет нам найти значение для текущего состояния? Ответ – мы должны рассмотреть текущую группу объектов и разделить её ещё на несколько видов. Рассмотрим три случая:
Если ни один из последних символов префиксов – не '*'. Тогда, очевидно, последний символ строки-ответа должен соответствовать обоим этим символам. Что означает, что если они являются двумя различными буквами, то множество ответов пусто (в этом случае мы храним inf, как длину кратчайшего ответа). В ином случае, без своего последнего символа строка-ответ подходит под префикс длины i - 1первого шаблона и под префикс длины j - 1 второго шаблона. Что означает, что существует взаимно-однозначное соответствие между множеством ответов для состояния dp[i][j] и множеством ответов для состояния dp[i - 1][j - 1]. И кратчайший ответ для dp[i][j] больше ответа дляdp[i - 1][j - 1] на один, т. е. dp[i][j] = dp[i - 1][j - 1] + 1.
Если оба последних символа префиксов – '*'. Тогда можно заметить, что среди всех ответов кратчайшим будет тот, где хотя бы одна из двух '*' соответствует в нём пустой строке (потому что иначе мы можем выкинуть несколько последних символов ответа и укоротить, оставив его валидным). Таким образом, мы можем разделить ответы/объекты, соответствующие состоянию dp[i][j] на три группы: те, где '*' из префикса первого шаблона заменяется на пустую строку, те, где '*' из префикса второго шаблона заменяется на пустую строку, и те, которые заведомо не кратчайшие. Мы знаем кратчайший ответ в первой группе (dp[i - 1][j]), мы знаем кратчайший ответ во второй группе (dp[i][j - 1]) и нам всё равно, что в третьей группе. Таким образом, в этом случаеdp[i][j] = min(dp[i - 1][j], dp[i][j - 1]).
Примечание: внимательный читатель мог заметить, что то, что мы считаем объектом в этой задаче – это в действительности не просто строка, соответствующая обоим шаблонам, а комбинация такой строки и такого соответствия (т. е., на какие конкретно символы были заменены '*', чтобы образовать эту строку).
Если только один из последних символов префиксов – '*'. Это самый интересный случай, где не очевидно, как можно узнать ответ, зная ответ для меньших подзадач. В таких случаях я рекомендую забыть об остальном и спросить себя вновь, какие объекты нас интересуют? Предположим, что префикс первого шаблона – s[0]s[1]...s[i - 1], s[i - 1] == '*', а префикс второго шаблона – t[0]t[1]...t[j - 1], t[j - 1] != '*'. В этом случае, мы конкретно хотим найти строку a[0]a[1]...a[n - 1], такую, что a[n - 1] равно t[j - 1] (или любой букве, если t[j - 1] = '?') и a[0]a[1]...a[n - 2] подходит под префикс второго шаблона длиной j - 1, и с другой стороны какой-то её префикс – возможно вся строка – подходит под префикс перого шаблона длины i - 1.
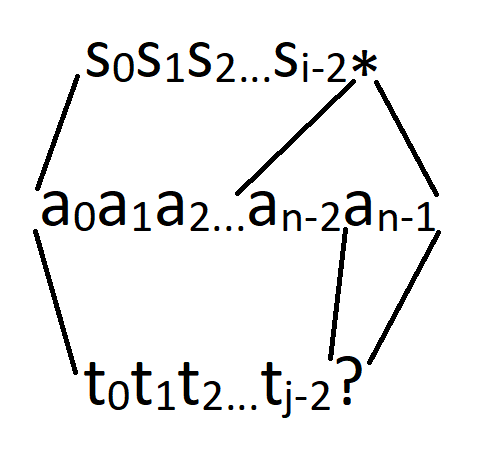
Первая часть условия – хорошая: "a[0]a[1]...a[n - 1] подходит под префикс втрого шаблона длины j - 1" означает, что мы можем обратиться к некому состоянию dp[...][j - 1], но что делать со второй частью? Мы можем сначала разобраться с очевидными случаями: когда '*' в первом шаблоне соответствует пустой строке в ответе – в этом случае длина кратчайшего такого ответа – это просто dp[i - 1][j].
Остаётся обработать лишь случай, когда '*' соответствует хотя бы одному символу, т. е. a[n - 1]. Но в таком случае a[0]a[1]...a[n - 2] подходит не только под префикс второго шаблона длины j - 1, но также и под префикс первого шаблона длины i, более того, существует взаимно-однозначное соответствие между объектами, которые нам осталось обработать, и объектами, соответствующими состоянию dp[i][j - 1]: каждая из требуемых строк может быть получена путём взятия некой строки, соответствующей dp[i][j - 1] и добавления к ней буквы t[j - 1] (или, допустим, буквы 'a', если t[j - 1] – это '?'). Это значит, что финальная формула в этом случае – это dp[i][j] = min(dp[i - 1][j], dp[i][j - 1] + 1).
Базовые состояния ДП – те, где i = 0 или j = 0, в этом случаеdp[i][j] равно либо0, если все символы в префиксах – это '*', либо inf в остальных случаях. Сложность работы – очевидно, O(|s| * |t|).
#include <bits/stdc++.h>
using namespace std;
#define int int64_t
int inf = 2e18;
int32_t main() {
ios_base::sync_with_stdio(0);
string s, t;
cin >> s >> t;
int n = s.size(), m = t.size();
vector<vector<int>> dp(n + 1, vector<int>(m + 1, inf));
// инициализируем базовые состояния
dp[0][0] = 0;
for (int i = 0; i < n; i++) {
if (s[i] != '*') {
break;
}
dp[i + 1][0] = 0;
}
for (int j = 0; j < m; j++) {
if (t[j] != '*') {
break;
}
dp[0][j + 1] = 0;
}
// заполним таблицу
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
char last_s = s[i - 1], last_t = t[j - 1];
if (last_s != '*' && last_t != '*') {
dp[i][j] = last_s != '?' && last_t != '?' && last_s != last_t
?
inf
:
dp[i - 1][j - 1] + 1;
} else if (last_s == '*' && last_t == '*') {
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]);
} else if (last_s == '*') {
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1] + 1);
} else {
dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1]);
}
}
}
if (dp[n][m] >= inf) {
cout << "No solution!\n";
return 0;
}
// восстановим ответ
string ans = "";
int i = n, j = m;
while (i > 0 && j > 0) {
char last_s = s[i - 1], last_t = t[j - 1];
if (last_s != '*' && last_t != '*') {
ans.push_back(last_s != '?' ? last_s : (last_t != '?' ? last_t : 'a'));
i--;
j--;
} else if (last_s == '*' && last_t == '*') {
if (dp[i - 1][j] < dp[i][j - 1]) {
i--;
} else {
j--;
}
} else if (last_s == '*') {
if (dp[i - 1][j] < dp[i][j - 1] + 1) {
i--;
} else {
ans.push_back(last_t != '?' ? last_t : 'a');
j--;
}
} else {
if (dp[i - 1][j] + 1 < dp[i][j - 1]) {
ans.push_back(last_s != '?' ? last_s : 'a');
i--;
} else {
j--;
}
}
}
reverse(ans.begin(), ans.end());
cout << ans << '\n';
}
607B - Zuma Дана последовательность чисел, вы можете удалить подряд-стоящий участок последовательности, если он является палиндромом. Найдите минимальное количество таких шагов, необходимых для удаления всей последовательности.
Глядя на ограничения, можно предположить, что параметры – это l и r, где dp[l][r] – это ответ для задачи, если бы существовал только полуинтервал последовательности с l включительно по r не включительно. Теперь надо подумать, как можно найти это значения, зная значения для всех вложенных полуинтервалов. Прежде всего, нужно определить, что в данном случае является объектом. Конечно, под объектом мы имеем в виду набор действий, ведущих к удалению всей строки. Иногда полезно визуально отобразить объект.
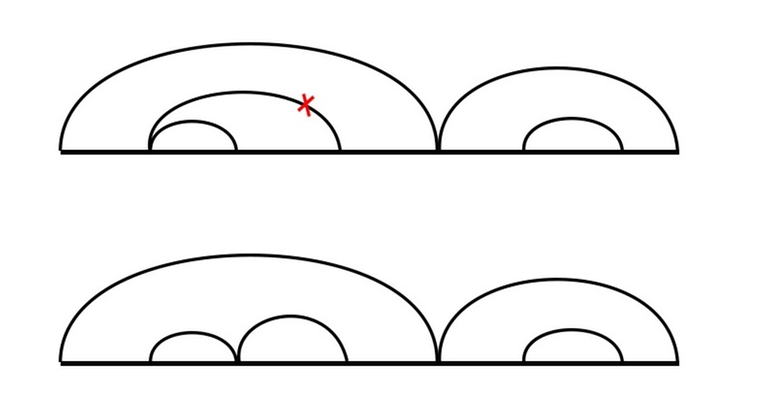
Давайте рисовать дугу над частями, которые удаляем. Дуга будет содержать другие дуги, соответствующие предыдущим удалениям вложенных частей. Давайте договоримся не рисовать дугу с l по r, если уже существует дуга с l по r' (r' < r), в этом случае мы могли бы просто нарисовать её от r' to r (так как остальное всё равно уже удалено). Аналогично будем поступать, если уже существует дуга сl' по r (l < l'). Таким образом, мы можем быть уверены, что крайний левый и крайний правый элементы под дугой удаляются тем непосредственно действием, соответствующий этой дуге.
Давайте последуем своему совету и сначала разберёмся с очевидными случаями. Для начала мы можем применить все переходы вида dp[l][r] = min(dp[l][r], dp[l][mid] + dp[mid][r]) (гдеl < mid < r), т. е. попробовать разделить интервал на два всеми возможными способами, и независимо удалить оба оптимальным способом, к счастью, ограничения позволяют сделать это.
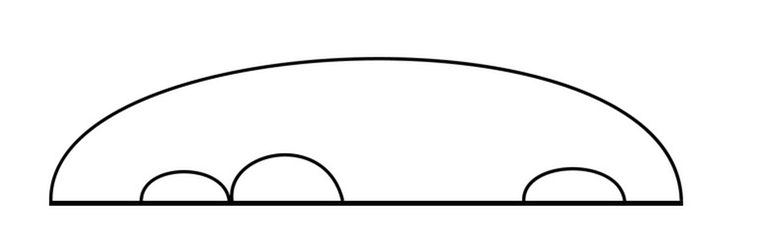
Объекты, непокрытые нами – это те, которые нельзя разделить на две независимые части, то есть те, у которых дуга накрывает всю последовательность, или те, у которых крайний левый и крайний правый элементы удаляются на самом последнем шаге. Прежде всего, это предполагает, что крайний левый и крайний правый элементы равны, так как мы можем удалять только палиндромы. Если они не равны, то мы уже покрыли все случаи сделанными переходами. Иначе, всё ещё требуется найти кратчайший набор действий, который заканчивается одновременным удалением крайнего левого и крайнего правого элементов участка. Последнее действие фиксировано и не зависит от нас. Общий совет: если что-то не зависит от вас, попробуйте это учесть и затем абстрагироваться.
Давайте переформулируем, какие объекты мы ищем, но теперь без упоминания последнего действия: набор обговоренных действий на данном участке последовательности, которые не затрагивают крайний левый и крайний правый элементы и ведут к тому, что данный участок последовательности становится палиндромом (чтобы было возможно осуществить последнее действие: удалить весь участок). Другими словами, мы хотим знать, какое минимальное количество действий нужно, чтобы сделать полуинтервал [l + 1, r - 1) палиндромом. Но это – конечно, dp[l + 1][r - 1] - 1, потому что каждый объект, соответствующий dp[l + 1][r - 1] – это по сути набор действий, приводящих к тому, чтобы этот участок стал палиндромом, а затем ещё одно действие, удаляющее его. Так что финальный переход, который нужно применить в случае, если c[l] = c[r - 1] – это dp[l][r] = min(dp[l][r], dp[l + 1][r - 1]) (сделать тот же самый набор действий, но в конце вместо удаления [l + 1, r - 1) удалить [l, r)).
Примечание: наша логика ломается, если r - l = 2, в этом случаеdp[l + 1][r - 1] = 0, так что мы не можем заменить последнее действие из набора. В этом случае dp[l][r] = 1 (если c[l] = c[r - 1]).
Базовые состояния ДП – это те, где r - l = 1, в этом случаеdp[l][r] равно 1. Сложность работы – O(n^3).
#include <bits/stdc++.h>
using namespace std;
#define int int64_t
int inf = 2e18;
int32_t main() {
ios_base::sync_with_stdio(false);
int n;
cin >> n;
vector<int> c(n);
for (int i = 0; i < n; i++) {
cin >> c[i];
}
vector<vector<int>> dp(n, vector<int>(n + 1, inf));
// инициализируем базовые состояния
for (int i = 0; i < n; i++) {
dp[i][i + 1] = 1;
}
// заполним таблицу
for (int len = 2; len <= n; len++) {
for (int l = 0; l + len <= n; l++) {
int r = l + len;
for (int mid = l + 1; mid < r; mid++) {
dp[l][r] = min(dp[l][r], dp[l][mid] + dp[mid][r]);
}
if (c[l] == c[r - 1]) {
if (len == 2) {
dp[l][r] = 1;
} else {
dp[l][r] = min(dp[l][r], dp[l + 1][r - 1]);
}
}
}
}
cout << dp[0][n] << endl;
}
Я надеюсь, что дал вам небольшое понимание, как легко придумать переходы в ДП с подзадачами. Если вам понравился пост, пожалуйста, поставьте лайк :)
Если хотите узнать больше, я напоминаю, что даю частные уроки по спортивному программированию, цена – $25/ч. Пишите мне в Telegram, Discord: rembocoder#3782, или в личные сообщения на CF.
Привет! Я получил хороший отлкик от сообщества Codeforces, поэтому я начинаю серию обучающих постов.
Сегодня я хочу рассказать об одной очень полезной классификации задач на динамическое программирование, к которой я пришёл за годы практики. Я не претендую на авторство этой идеи, но я ни разу не видел, чтобы она где-то явно выражалась, так что я введу собственные термины. Назовём это "ДП по подзадачам" (или "Обычное ДП") и "ДП с симуляцией процесса". Сегодня я сосредоточусь на последнем.
Как вам рассказали о ДП? В каких терминах? Когда я учился в школе, мне объяснили, что ДП – это просто разбиение задачи на подзадачи. Сначала вы вводите параметры в задачу. Набор значений по каждому параметру называется состоянием ДП, оно соответствует конкретной подзадаче. Затем вам всего лишь надо найти ответ для каждого состояния / подзадачи, и знание ответа для меньших подзадач должно помочь вам найти ответ для текущей. Рассмотрим пример:
AtCoder DP Contest: Задача L Два игрока играют на массиве чисел. Они по очереди берут либо самый левый, либо самый правый из оставшихся элементов массива, пока он не опустеет. Каждый старается максимизировать сумму взятых им элементов. Какая будет разница между счетами первого и второго игроков, если они играют оптимально?
Чтобы решить эту задачу, нужно ввести два параметра: l и r, где dp[l][r] – это ответ на эту же самую задачу, но если бы мы рассматривали только числа с полуинтервала [l, r). Как его посчитать? Вы просто сводите задачу к её подзадачам. Есть два возможных хода первого игрока: взять самое левое число или самое правое число. В первом случае остаётся полуинтервал [l + 1, r), во втором случае – полуинтервал [l, r - 1). Но если мы считаем значение dp по всем полуинтервалам в порядке возрастания длины, то к этому моменту мы уже знаем исход игры в обоих случаях: это a[l] - dp[l + 1][r] и a[r - 1] - dp[l][r - 1]. И так как первый игрок хочет максимизировать разницу, то он выберет максимальное из этих двух чисел, значит итоговая формула — dp[l][r] = max(a[l] - dp[l + 1][r], a[r - 1] - dp[l][r - 1]).
Здесь объясенние через подзадачи работает идеально. И я не буду скрывать, любую задачу на ДП можно решить в таких терминах. Но ваша эффективность сильно повысится, если вы научитесь и другому подходу, который я назову симуляцией процесса. Так что это значит?
Этот подход в основном используется в задачах, где вас просят либо "посчитать число объектов такого вида" или "найти лучший объект такого вида". Идея в том, чтобы придумать некий пошаговый процесс, который строит такой объект. Каждый путь процесса (т.е. последовательность шагов) должен соответсвовать одному объекту. Взглянем на пример.
118D - Легионы Цезаря. После формализации задача звучит так:
Посчитайте количество последовательностей из 0-й и 1-ц, где ровно n0 0-й и ровно n1 1-ц, при этом запрещено иметь более k0 0-й подряд или более k1 1-ц подряд.
Задачи на последовательности – наиболее очевидные кандидаты на симуляуию процесса. В таких задачах процессом обычно является просто "Выпишите последовательность слева направо", по одному элементу на каждом шагу. В данном случае есть два возможных шага: выписать 0 или 1 справа от того, что уже написано. Однако, мы должны допускать только корректные последовательности, поэтому некоторые шаги придётся запретить. Для этого мы вводим параметры процесса. Параметры должны:
Определять, какие шаги на данный момент позволены.
Быть пересчитываемыми после совершения шага.
Отсекать валидные конечные состояния от невалидных.
В данном случае есть следующие правила:
Не более n0 0-й всего.
Не более n1 1-ц всего.
Не более k0 0-й подряд.
Не более k1 1-ц подряд.
Поэтому нам потребуется знать следующие параметры процесса:
Сколько уже выписано 0-й.
Сколько уже выписано 1-ц.
Какой последний выписанный символ.
Сколько таких символов написано сейчас на конце подряд.
Если мы знаем, чему равны эти параметры, у нас есть вся необходимая информация, чтобы определить, можем ли мы написать ещё один 0 или ещё одну 1, а также пересчитать параметры после того, как совершится один из этих шагов. Когда мы используем этот подход, в массиве dp просто хранится некая информация о всех путях процесса, приводящих в данное состояние (где под состоянием я также имею в виду набор значений для каждого параметра). Если мы хотим сосчитать количество способов выполнить процесс, эта информация будет просто количеством подобных путей. Если мы хотим найти "наилучший" способ совершить процесс, мы храним некую информацию о наилучшем пути среди всех, что приводят в данное состояние, например, его цену или последний шаг на таком пути, если мы хотим позже восстановить ответ.
И вот главный трюк: каждый переход в графе ДП – это шаг процесса при некотором состоянии. Когда мы реализуем переход из состояния A в состояние B, мы просто должны обработать все ново-найденные пути, полученные продлением всех путей, ведущих в A, шагом, ведущим их в B. Это не все пути, заканчивающиеся в B, но идея в том, что вы должны обнаружить их всех к моменту, когда начнёте реализовать переходы из B. Если в dp хранится число таких путей, то реализовать переход – означает просто прибавить dp[A] к dp[B], то есть прибавить все ново-найденные пути, попадающие в B через A, к общему количеству путей, кончающихся в B.
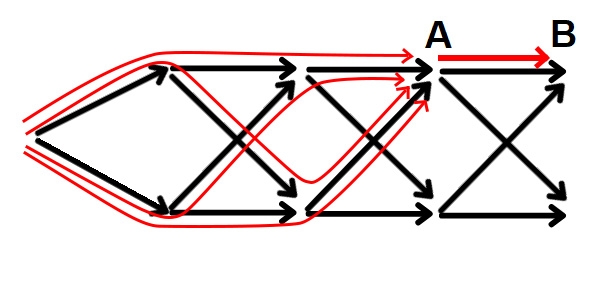
Если вы когда либо слышали о ДП с переходами вперёд и ДП с переходами назад, вы могли начать подозревать, что эта классификация – и есть та, что я здесь описываю. Однако, я считаю, что классификация переходы вперёд и переходы назад относится лишь реализации. Реализация с переходами назад – это: "Зафиксируем состояние, которое ещё не было посчитано, реалзиуем все переходы, ведущие в него"; тогда как с переходами вперёд – это: "Зафиксируем состояние, что уже было посчитано, реализуем все переходы, исходящие из него".
На самом деле, после того, как вы определились с графом ДП, не важно в каком порядке вы реализуете переходы. Вы можете даже придумать свой способ, если следуете простому правилу: не реализуйте переход из состояния A раньше перехода в состояние A. Но всё же подход с переходами вперёд намного более применим и осмысленен для симуляции процесса, а переходы назад – для обычного ДП, так что эти классификации в 90% случаев совпадают.
Давайте вернёмся к нашей задаче и реализуем решение. Для этого надо определить стартовое состояние процесса. Обозначим за dp[i][j][t][k] состояние, где уже i 0-й, j 1-ц, последний символ – t, и он написан k раз подряд на конце. Очевидно, мы начинаем при i = 0 и j = 0, но чему равны t и k? Строго говоря, если мы начинаем с пустой последовательности, "последнего символа" не существует. Но давайте слегка поменяем описание процесса и скажем, что когда мы начинаем, последним символом считается 0, но он был выписан 0 раз подряд. Так что начальное состояние – dp[0][0][0][0], и начать мы можем только одним способом, так что dp[0][0][0][0] должно быть равно 1.
Остальное довольно просто и интуитивно:
#include <bits/stdc++.h>
#define int int64_t
using namespace std;
int mod = 1e8;
int dp[101][101][2][11];
int32_t main() {
ios_base::sync_with_stdio(0);
int n0, n1, k0, k1;
cin >> n0 >> n1 >> k0 >> k1;
dp[0][0][0][0] = 1;
for (int i = 0; i <= n0; i++) { // переберём все состояния
for (int j = 0; j <= n1; j++) { // начиная со стартового
for (int t = 0; t < 2; t++) { // в топологическом порядке
int k = t == 0 ? k0 : k1;
for (int l = 0; l <= k; l++) {
// фиксируем состояние dp[i][j][t][k]
if (i < n0 && (t == 1 || l < k)) { // можем ли мы выписать ещё один 0?
// если да, то окажемся в этом состоянии
(dp[i + 1][j][0][t == 1 ? 1 : l + 1] += dp[i][j][t][l]) %= mod;
}
if (j < n1 && (t == 0 || l < k)) { // можем ли мы выписать ещё одну 1?
// если да, то окажемся в этом состоянии
(dp[i][j + 1][1][t == 0 ? 1 : l + 1] += dp[i][j][t][l]) %= mod;
}
}
}
}
}
int ans = 0;
for (int t = 0; t < 2; t++) {
int k = t == 0 ? k0 : k1;
for (int l = 0; l <= k; l++) {
// фиксируем одно из корректных финальных состояний процесса
(ans += dp[n0][n1][t][l]) %= mod;
}
}
cout << ans << endl;
}
Очевидно, временная сложность будет равна количество переходов в графе ДП. В данном случае это O(n0 * n1 * (k0 + k1)).
543A - Пишем код Есть n программистов, они должны написать m строк кода сделав не более b ошибок. i-й программист совершает a[i] ошибок за строку. Сколько есть способов это сделать? (Два способа различаются, если различается количество строк, написанных одним из программистов).
Давайте определим процесс, который строит такой объект (корректное распределение m строк кода между n программистами). В условии задачи этот объект был представлен, как последовательность чисел v[1], v[2], ..., v[n] (где v[i] – число строк, написанное i-м программистом), как будто они намекают нам, что это очередная задача на построение последовательности. Давайте попробуем определить шаг процесса, как "написать очередной элемент последовательности", слева направа.
Чтобы последовательность получилась корректной, должны выполняться эти правила:
Длина последовательности – n.
Сумма элементов равна m.
Сумма a[i] * v[i] по всем элементам не превосходит b.
Значит, нам нужны следующие параметры:
Количество уже выписанных элементов (количество зафиксированных программистов).
Сумма уже выписанных элементов (количество написанных строк кода).
Сумма a[i] * v[i] для всех уже выписанных элементов (количество совершённых ошибок).
Число состояний такого процесса будет в районе n * m * b. Но из каждого состояния в среднем будет порядка m / 2 переходов, а именно: "выписать 0", "выписать 1", "выписать 2", ..., "выписать m - s (где s – это текущая сумма)". Так что общее число переходов будет O(n * m^2 * b), что не пройдёт ограничение по времени. Это учит нас тому, что не всегда стоит использовать процесс, описанный в условии, надо мыслить шире.
Давайте придумаем другой процесс. Возможно, вместо того, чтоб идти по программистам, надо идти по строкам? Давайте для каждой строки определим, какой программист её напишет. Чтобы не посчитать одно и то же распределение дважды, скажем, что первый программист пишет первые v[1] строк, второй пишет v[2] следующих строк, и т. д. Так что если строку написал i-й программист, следующую строку могут написать лишь i-й, i + 1-й, ..., n-й. Тогда нам потребуются следующие параметры:
Сколько уже написано строк.
Какой программист написал последнюю строку.
Сколько уже сделано ошибок.
И снова та же проблема: есть около n * m * b состояний и в среднем порядка n / 2 переходов из каждого состояния, а именно: "следующую строку пишет программист i", "следующую строку пишет программист i + 1", ..., "следующую строку пишет программист n". Так что временная сложность будет O(n^2 * m * b), что опять слишком долго.
Если подумать какое-то время, то станет очевидно, что нам в любом случае потребуются эти три параметра: что-то про число программистов, что-то про число строк и что-то про число ошибок. Так что если мы хотим пройти ограничение по времени, нам необходимо сократить количество переходов из каждого состояния, сделать его O(1). Нам явно требуется как минимум два перехода: один будет увеличивать параметр строк, другой будет увеличивать параметр программистов. Если мы подумаем над этим, то получим такой процесс: "В начале за столом сидит программист 1. На каждом шаге либо текущий программист пишет одну строку кода, либо текущий программист уходит, а вместо него за стол садится следующий". Параметры:
Какой программист сейчас за столом.
Сколько уже написано строк.
Сколько уже сделано ошибок.
Начальное состояние: первый программист сидит за столом, написано 0 строк, сделано 0 ошибок. Число переходов – наконец, O(n * m * b). Чтобы сократить потребление памяти, я использую мнимый параметр (это означает, что я храню dp только для текущего значения первого параметра, забывая предыдущие слои). Реализация:
#include "bits/stdc++.h"
#define int int64_t
using namespace std;
int mod;
void add(int& a, int b) { // вместо (a += b) %= mod
a += b;
if (a >= mod) {
a -= mod;
}
}
int32_t main() {
ios_base::sync_with_stdio(0);
int n, m, b;
cin >> n >> m >> b >> mod;
vector<int> a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
vector<vector<int>> dp(m + 1, vector<int>(b + 1)); // текущий слой (изначально 0)
dp[0][0] = 1;
for (int i = 0; i < n; i++) {
vector<vector<int>> new_dp(m + 1, vector<int>(b + 1)); // следующий слой (i + 1)
for (int j = 0; j <= m; j++) {
for (int k = 0; k <= b; k++) {
// фиксируем состояние dp(i)[j][k], где i мнимое
if (i < n - 1) { // есть ли следующий программист?
// если есть, посадим его за стол, окажемся в таком состоянии
add(new_dp[j][k], dp[j][k]);
}
if (j < m && k + a[i] <= b) { // может ли текущий программист написать строчку?
// если может, окажемся в данном состоянии
add(dp[j + 1][k + a[i]], dp[j][k]);
}
}
}
if (i < n - 1) {
dp = new_dp; // перейти к слою i + 1
}
}
int ans = 0;
for (int k = 0; k <= b; k++) {
// фиксируем одно из корректных финальных состояний процесса
// (последний программист сидит за столом, все строки написаны)
add(ans, dp[m][k]);
}
cout << ans << endl;
}
AtCoder DP Contest: Задача D Есть n объектов, i-й имеет вес w[i] и цену v[i]. Какая максимальная сумма цен по всем наборам объектов с суммой весов не более m?
Шаг процесса – это просто: "Посмотрим на следующий объект и либо пропустим его, либо возьмём". Параметры:
Сколько объектов мы уже рассмотрели.
Сумма весов взятых объектов.
Первый параметр снова будет мнимым, так что мы храним лишь один слой таблицы dp, соответствующий зафиксированному значению первого параметра. Значение dp – максимальная сумма цен взятых объектов по всем путям процесса, ведущим в данное состояние. Реализация:
#include <bits/stdc++.h>
using namespace std;
#define int int64_t
void relax(int& a, int b) {
a = max(a, b);
}
int32_t main() {
ios_base::sync_with_stdio(0);
int n, m;
cin >> n >> m;
vector<int> w(n), v(n);
for (int i = 0; i < n; i++) {
cin >> w[i] >> v[i];
}
vector<int> dp(m + 1, -2e18); // если в состояние не ведёт ни один путь, максимальной ценой считается -inf
dp[0] = 0;
for (int i = 0; i < n; i++) {
vector<int> new_dp = dp; // автоматически реализуем все переходы первого вида
for (int j = 0; j <= m - w[i]; j++) {
// фиксируем состояние dp(i)[j], где i мнимое
relax(new_dp[j + w[i]], dp[j] + v[i]); // переход второго вида
}
dp = new_dp; // переходим от слоя i к i + 1
}
int ans = -2e18;
for (int i = 0; i <= m; i++) {
relax(ans, dp[i]); // фиксируем сумму весов
}
cout << ans << endl;
}
Есть множество примеров, где этот подход значительно упрощает поиск решения, но я не могу привести все. Если понравился пост, нажмите пожалуйста лайк :)
Если хотите узнать больше, я напоминаю, что даю частные уроки по спортивному программированию, цена – 1800 руб/ч. Пишите мне в Telegram, Discord: rembocoder#3782, или в личные сообщения на CF.
Всем привет!
Меня зовут Александр Мокин. Последние три года в качестве основной работы я преподаю спортивное программирование.
Я был победителем Всероссийской олмипиады по информатике в 2012, призёром – в 2011 и 2013. В 2018 я стал финалистом чемпионата по программированию ICPC.
В 2019 я начал преподавать и помог десяткам людей продвинуться и достичь своих целей (смотри отзывы). За это время я разработал свой подход. Я не только провожу людей по пресловутым алгоритмам, но и учу конкретным техникам для решения реальных задач, а также быстро писать работающий код.
Теперь я хочу выйти на другой уровень. Я обращаюсь к мировой аудитории: не стесняйтесь писать мне в Facebook, Telegram, личные сообщения или на е-мэйл: rembocoder@gmail.com. Базовая цена: $30/ч.
Если я получу достаточно фидбэка, я обещаю создать YouTube-канал, посвящённый СП, писать статьи, создавать бесплатные курсы и учебники. Так что если вам не нужны частные уроки, пожалуйста, всё равно плюсаните этот пост, чтобы кто-то смог найти учителя, а Codeforces получил контрибьютора на полную ставку. Иначе мир пополнит очередной скучный работник FAANG.
Спортивное программирование – это моя моя страсть, помогите мне исполнить мечту!
| Название |
|---|


