CodeChef invites you to participate in the March Cook-off 2015 at http://www.codechef.com/COOK56.
Time: 22nd March 2015 (2130 hrs) to 23rd March 2015 (0000 hrs). (Indian Standard Time — +5:30 GMT) — Check your timezone.
Details: http://www.codechef.com/COOK56/
Registration: Just need to have a CodeChef user id to participate.
New users please register here
- Problem Setter : Vitaliy Herasymiv
- Editorialist: Amit Pandey
- Problem Tester: Istvan Nagy
- Contest Admin: Praveen Dhinwa
- Russian Translator : Sergey Kulik
- Mandarin Translator: Gedi Zheng
It promises to deliver on an interesting set of algorithmic problems with something for all.
The contest is open for all and those, who are interested, are requested to have a CodeChef userid, in order to participate.









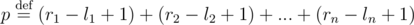 .
. 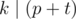 . Несложно убедится, что
. Несложно убедится, что 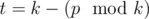 .
. 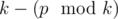 недостаточно: нужно отдельно рассмотреть случай когда
недостаточно: нужно отдельно рассмотреть случай когда 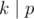 , или просто вывести
, или просто вывести 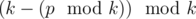 .
.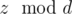 не изменится. Действительно
не изменится. Действительно 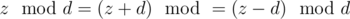 . Поэтому необходимым условием существования ответа есть условие, что все
. Поэтому необходимым условием существования ответа есть условие, что все 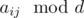 равны между собой. Несложно убедится, что это будет и достаточное условие (это также видно по алгоритму описанному ниже).
равны между собой. Несложно убедится, что это будет и достаточное условие (это также видно по алгоритму описанному ниже).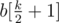 , то есть к медиане массива. Почему именно к медиане? Предположим, что свели не к медианному элементу с номером
, то есть к медиане массива. Почему именно к медиане? Предположим, что свели не к медианному элементу с номером 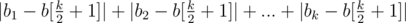 , разделенная на
, разделенная на 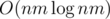 .
.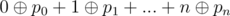 максимально возможная.
максимально возможная.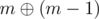 не пропадет ни один бит, при
не пропадет ни один бит, при  не пропадет ни один бит, ..., при
не пропадет ни один бит, ..., при 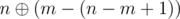 не пропадет ни один бит. Поэтому, нам стоит именное такие числа присвоить перестановке (то есть
не пропадет ни один бит. Поэтому, нам стоит именное такие числа присвоить перестановке (то есть 
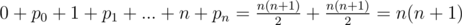 .
.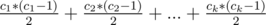 . То есть, если перебирать такие пути, достаточно воспользоватся этой формулой что-бы найти ответ. Но такой алгоритм —
. То есть, если перебирать такие пути, достаточно воспользоватся этой формулой что-бы найти ответ. Но такой алгоритм — 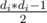 по всем другим вершинам что выходят из текущей (но кроме той которой мы рассматриваем), умноженное на количество вершин поддерева (не всего текущего, а только того что выходит из ребра что перебираем). Это удобно реализуется, используя частичные суммы для оптимизации (что-бы все время не пересчитывать сумму). Для остальных вершин (тех что не в поддереве) все аналогично, но немножко сложнее. Тут можно, например, в dfs-е поддерживать параметр, который равен ответу для текущей вершины. Потом, когда по ребру спускаемся вниз по дереву, нужно обновить результат как это было и в первом случае, но уже с количество вершин равным
по всем другим вершинам что выходят из текущей (но кроме той которой мы рассматриваем), умноженное на количество вершин поддерева (не всего текущего, а только того что выходит из ребра что перебираем). Это удобно реализуется, используя частичные суммы для оптимизации (что-бы все время не пересчитывать сумму). Для остальных вершин (тех что не в поддереве) все аналогично, но немножко сложнее. Тут можно, например, в dfs-е поддерживать параметр, который равен ответу для текущей вершины. Потом, когда по ребру спускаемся вниз по дереву, нужно обновить результат как это было и в первом случае, но уже с количество вершин равным 

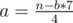 . Среди всех пар
. Среди всех пар 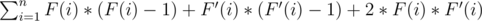
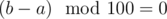 .
.
