Я обнаружил небольшую нехватку материалов на эту тему и хочу начать со статьи rationalex:
Задача
Хотим научиться сравнивать корневые деревья на изоморфизм (равенство с точностью до перенумерования вершин + корень одного дерева обязательно переходит в корень другого дерева).
Хеш вершины
Заметим, что поскольку мы не можем аппелировать к номерам вершин, единственная информация, которую мы можем оперировать — это структура нашего дерева.
Положим тогда хешем вершины без детей какую-нибудь константу (например, 179), а для вершины с детьми положим в качестве хеша некоторую функцию от отсортированного (поскольку мы не знаем истинного порядка, в котором дети должны идти, нужно привести их к одинаковому виду) списка хешей детей. Хешом корневого дерева будем считать хеш корня.
По построению, у изоморфных корневых деревьев хеши совпадают (доказательство индукцией по числу уровней в дереве автор оставляет читателю в качестве упражнения).
Полиномиальный хеш не подходит
Рассмотрим 2 дерева:
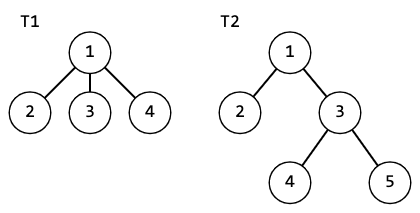
Если мы посчитаем для них в качестве функции от детей взять полиномиальный хеш, то получим: $$$h(T1)=179+179p+179p^2=179+p(179+179p)=h(T2)$$$
Какую же хеш-функцию взять?
В качестве хорошей хеш-функции подойдёт, например
Для этой хеш-функции может показаться, что можно не сортировать хеши детей, однако это не так, потому что при вычислении чисел с плавающей точкой у нас возникает погрешность, и чтобы это результат суммирования был одинаковый для изоморфных деревьев, суммировать детей надо тоже в одинаковом порядке.
Пример более complicated хеш-функции:
Асимптотика
Всё что нам нужно делать на каждом уровне — это сортировка вершин по значению хеша и суммирование, так что итоговая сложность: $$$O(|V| log(|V|))$$$
Хочу продолжить от себя:
В реалиях Codeforces у данных подходов есть проблемы в виде взломов (что можно увидеть, например, по взломам этой задачи). Поэтому хочу рассказать о подходе, при котором не возникает коллизий.
Что же за хэш-функция?
Давайте для вершины отсортируем хэш-функции детей и сопоставим этому массиву номер (если он новый, то присвоим ему минимальный незанятый номер, иначе возьмём тот который уже дали).
Почему это работает быстро?
Легко заметить, что суммарный размер массивов, которые мы посчитали, равен $$$n - 1$$$ (каждое добавление это переход по ребру). Благодаря этому, даже используя для сопоставления treemap, на все обращения к нему потребуется суммарно $$$O(|V|log(|V|))$$$.







