So, a few months ago, I was working on Euler Tour from the usaco guide website. There, they explained how you could compress a tree into an array of start[] and end[] arrays to build a segment tree on top of it. However, with LCA (least common ancestor, they built a RMQ (range minimum query) segtree off of the full inorder traversal of the tree, which confused me greatly. After all, in the examples of summing subtrees and updating vertexes, we hadn't needed to do that. Additionally, I was still greatly uncomfortable with changing the size of the segtree, and a segtree with 2 * (2n-1) memory (I use the iterative version) pissed me off. I gave up and went back to dynamic programming.
Yesterday, however, I returned. The most annoying thing, in my opinion, was how the start[] and end[] arrays were combined so the segtree could be built, and there were two ways to do the euler tour I had to remember. Indeed, in my code I wrote the following:
So, I present a way to build the segtree off of only the start[] array. To understand this, make sure you know point update range sum segtree (I don't know fenwick tree/BIT but it likely also works here) and how to solve, say, Subtree Queries on CSES, or have read the corresponding section (18.2) in CPH.
To see why this works, let's take a look at an example.
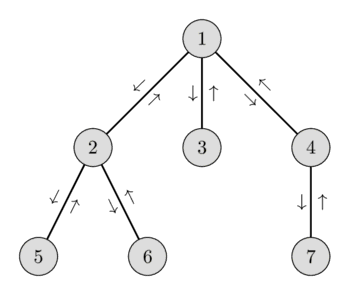
The corresponding array we build off of (and the depths):
Essentially what we are building off of is the first array, where the nodes are ordered by when we first meet them in the dfs traversal. Then: To find the LCA of two nodes, if any of the two is not within the others subtree, then the LCA is the parent node of the RMQ (based on depth, of course) in the range between the two. The parent node will not be present in this range, because it must have already been visited before. Proof of correctness is left to the reader, as always, for the author is forever typing at 12:22 am (I am sure, however, the proof is simple).
So, is this any better than before? We built on a segtree of half the size, after all.
Well, not really. Because segtree operations take O(log N) after processing, actually, we are reducing the time per query by O(1). And likely because we are adding a vector to track the parent of each vertex, it isn't any faster. Memory isn't any better, either.
So what's the use?
Now, at least, there aren't two ideas for euler tour running inside my head. I just understand that I can use start[] and stop[] arrays for this. It's mostly for simplicity, really. And because I'm doing usaco guide, I probably won't learn binary lifting until later, as it's in platinum.
This was just a fun thing to think about and do. Open to any code simplifications and blog criticisms! It's my first time writing one. Thanks to iframe_ for helping optimize it, and thank you for reading!






