I recently know about Strassen's aproach in multiplying matrices, which i find very clever and interesting. So i decided to share it. Hope this help :))) People usually use the naive n^3 method to multiply a n*x and y*n matrix. Which mean the maximum size of n is about 500. But Strassen find a way to do so in n^log2(7) which is about n^2.8, which mean it will bring the maximum size of n to about 750. First, we divide the matrix in to smaller matrix. Let consider a 2*2 matrix.  The result of this matrix will be
The result of this matrix will be 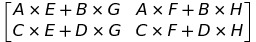 And if A,B,C,D,E,F,G,H are all matrices of size n*n, it is still remain correct. So we will multiply these matrices by using divide and conquer, divide them into smaller pieces and conquer them. Each time we multiply two matrices, we divide them into 2*2 matrices and calculate them.
And if A,B,C,D,E,F,G,H are all matrices of size n*n, it is still remain correct. So we will multiply these matrices by using divide and conquer, divide them into smaller pieces and conquer them. Each time we multiply two matrices, we divide them into 2*2 matrices and calculate them.
Let consider a 2*2 matrix, regularly we need 8 multiplications to multiply 2 2*2 matrix. But Strassen find a way to do so in just 7 multiplications so it will reduce the complexity from n^log2(8)(which is n^3) to n^log2(7). So now i will describe the way he multiply 2*2 matrices with 7 multiplications. E G F H A x x B x x C x x D x x
→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
4 дня
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
4 дня
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
→ Найти пользователя
→ Прямой эфир
Fast matrix multiplication
Правка en1, от Chi_Bach, 2015-12-31 06:19:11
История
Правки


| Rev. | Язык | Кто | Когда | Δ | Комментарий | |
|---|---|---|---|---|---|---|
| en8 |

|
Chi_Bach | 2015-12-31 19:20:03 | 161 | ||
| en7 |

|
Chi_Bach | 2015-12-31 09:20:53 | 29 | Tiny change: 'ubtraction, so it is' -> 'ubtraction compare to the naive aproach, so it is' | |
| en6 |

|
Chi_Bach | 2015-12-31 09:18:48 | 1377 | ||
| en5 |

|
Chi_Bach | 2015-12-31 08:51:02 | 1150 | Tiny change: '1UhyOqP)\n' - (published) | |
| en4 |

|
Chi_Bach | 2015-12-31 08:24:50 | 1402 | Tiny change: '---+---+\n\n| | E ' - | |
| en3 |

|
Chi_Bach | 2015-12-31 07:08:35 | 116 | ||
| en2 |

|
Chi_Bach | 2015-12-31 06:23:03 | 72 | Tiny change: 'lp :))).\nPeople u' - | |
| en1 |

|
Chi_Bach | 2015-12-31 06:19:11 | 1334 | Initial revision (saved to drafts) |
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 26.11.2024 12:35:48 (k2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|




