Hello Codeforces. Today I'm writing about a Math topic that is simple, but resources and problems are limited.
SLAE stands for system of linear equations. Basically, consider we have a set of equations of the form :
a0·x0 + a1·x1 + a2·x2 + ... + an - 1·xn = m
b0·x0 + b1·x1 + b2·x2 + .... + bn - 1·xn - 1 = n
c0·x0 + c1·x1 + c2·x2 + .... + cn - 1·xn - 1 = o
.....
Note that all a, b, c... are real-valued arrays and all m, n, o are arbitrary reals. Realize how x0, x1, ...xn - 1 appear in each of the equations.
Now, we want to find values of [x0, x1...xn - 1] that satisfy each of the given equations listed. The simplest method to find such solutions is to use Gaussian Elimination, that solves the problem in O(N3), where N = number of equations = number of variables .
To Learn about Gaussian Elimination, click here. Today, we shall learn about 2 special class of problems that can be solved using Gaussian Elimination for SLAE.
Problem 1 : Markov Chains and Cyclic Expected Values :
Many a times as a part of expected value problems, you are expected to sum up infinite series that hold as limits, as probabilities lie in the closed interval [0, 1]. For example,
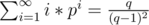 , as
, as 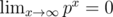
However, not always can we expect the variables whose Expected value we need to calculate to be independent. Consider you have N random variables 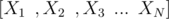 , where , there are cyclic dependencies among the variables for their expected values, i.e consider E(X1) depends on E(X2), E(X2) on E(X3) and E(X3) depends on E(X1). For example, consider the following problem :
, where , there are cyclic dependencies among the variables for their expected values, i.e consider E(X1) depends on E(X2), E(X2) on E(X3) and E(X3) depends on E(X1). For example, consider the following problem :
You are given Tree T consisting of N nodes. Initially there is a player in node S. In a single move, he moves to one of the adjacent nodes of the node he is currently at, each with equal probability. What is the expected number of moves before he reaches node T ?.
Here, we need to understand that the probabilities are infinite as well as cyclic. Creating a simple formula for the answer is quite hard. The Expected value starting from node S depends on some neighbor of node S, however, the Expected value of some neighbor of node S depends on Expected value of node S. Notice that we can create a transition matrix, as the procedure conducted on the tree is a Markov chain.
Create a matrix P, where P[i][j]= probability of moving from node i to j in a single move. Now, Let E(i) denote the expected number of steps needed to reach node T from node i.
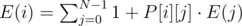 .
.
Try and take a moment and think about why this formula is correct.
Surprise Surprise, this can be modeled as SLAE. Rewrite equations as :
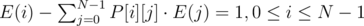 . So the system is :
. So the system is :
\begin{equation} \begin{pmatrix} 1-P[0][0] & -P[0][1] & ... & -P[0][N-1] \newline -P[1][0] & 1-P[1][1] & ... & -P[1][N-1] \newline .... \newline -P[N-1][0] & -P[N-1][1] & ... & 1-P[N-1][N-1] \end{pmatrix} \cdot \begin{pmatrix} E(0) \newline E(1) \newline . \newline . \newline E(n-1) \end{pmatrix} = \begin{pmatrix} 1 \newline 1 \newline .. \newline 1 \end{pmatrix} \end{equation}
This is the equation (IN - P)·E = 1,We need to find E. Note that for node T, we need to have P[t][i] = 0, t ≠ i and P[t][t] = 1, as we won't move from node T, it is an absorbent state of the markov chain. So, the Tth row of matrix IN - P will be all zeros. Just remove it from both sides of the equation.
Now, to find the E(i)'s, just take the matrix to RREF, to get the expected values. We have obtained E(i) for all 0 ≤ i ≤ N - 1, i ≠ T
We can use this generic technique in all cases where the expected values are cyclic in nature , i.e expected value of state A depends on state B, and expected value of state B depends on state A. We can use any prime mod too, to obtain expected value in Modulo.
Practice Problems :
One (Same problem as above) My Code
Problem 2 : Xor's using SLAE
Pr-requisite : Vector Space properties, Linear Algebra.
Without reading the link, proceed at your own risk.
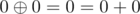 mod 2
mod 2
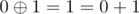 mod 2
mod 2
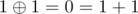 mod 2
mod 2
So, xor is just bit-wise addition mod 2. We can represent the xor of two integer's x, y as vector addition in  . For example ,
. For example ,
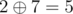 i.e. ,
i.e. ,
\begin{equation} \begin{pmatrix} 0 \newline 1 \newline 0 \end{pmatrix} + \begin{pmatrix} 1 \newline 1 \newline 1 \end{pmatrix} \equiv \begin{pmatrix} 1 \newline 0 \newline 1 \end{pmatrix}
Mod \space 2
\end{equation}
So, we can use this addition to replace xor.The main advantage of this scheme is that we can find easily whether , given a subset X, if there exists a subset of these numbers having xor equal to a given number Q. Note that the span of any given set of size N is a vector space. There is a concept called as Basis of a vector space , i.e a smallest size set subset of the given set that spans the entire vector space spanned by the original set given.
We can solve useful xor based problems such as :
1> Given a set S of size N, find the number of distinct integers that can be represented using xor over the set of the given elements.
2> How many subsequences of a given set S of size N have xor equal to X. (Do it yourself).
All of these problems can be modeled using SLAE in Mod 2. We can do operations faster in Mod 2 using bitset having complexity 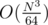 .
.
Problems :






