Hello Codeforces.
SLAE stands for system of linear equations. Basically, consider we have a set of equations of the form :
a0·x0 + a1·x1 + a2·x2 + ... + an - 1·xn = m
b0·x0 + b1·x1 + b2·x2 + .... + bn - 1·xn - 1 = n
c0·x0 + c1·x1 + c2·x2 + .... + cn - 1·xn - 1 = o
.....
Note that all a, b, c... are real-valued arrays and all m, n, o are arbitrary reals. Realize how x0, x1, ...xn - 1 appear in each of the equations.
Now, we want to find values of [x0, x1...xn - 1] that satisfy each of the given equations listed. The simplest method to find such solutions is to use Gaussian Elimination, that solves the problem in O(N3), where N = number of equations = number of variables .
To Learn about Gaussian Elimination, click here. Today, we shall learn about 2 special class of problems that can be solved using Gaussian Elimination for SLAE.
Problem 1 : Markov Chains and Cyclic Expected Values :
Many a times as a part of expected value problems, you are expected to sum up infinite series that hold as limits, as probabilities lie in the closed interval [0, 1]. For example,
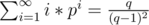, as ix -> 0, as x -> ∞ .
However, not always can we expect to reach such simple sums. Consider the following example :
